Быстрая подготовка метода опорных векторов последовательной минимальной оптимизации

12.1 Введение

SVM (Training a Support Vector Machine – Обучение опорных векторов) начинают все больше использоваться в машинном обучении и машинном видении научных кругов. Тем не менее, SVM еще не пользовались широким распространением в инженерном сообществе. Есть две возможные причины ограниченного использования инженерами. Во-первых, подготовка SVMs очень медленная, особенно для больших задач последовательной минимальной оптимизации. Во-вторых, алгоритмы обучения SVM сложные, тонкие, а иногда трудно реализуемые. В этой главе описывается новый алгоритм обучения SVM, который концептуально простой, легкий в реализации, и зачастую быстрее. Новый алгоритм обучения SVM называется последовательной минимальной оптимизацией (или SMO). В отличие от предыдущих SVM алгоритмов обучения, в которых используется численное квадратичное программирование (QP) в качестве внутреннего контура, SMO использует аналитический шаг QP. Поскольку SMO проводит большую часть времени для оценки решающей функции, а не выполняет QP, он может использовать наборы данных, которые содержат значительное количество нулевых элементов. В этой главе, эти данные множества называются редкими. SMO работает особенно хорошо для разреженных наборов данных, либо бинарных или недвоичных входных данных.

В этой главе рассматриваются современные RST алгоритмы обучения SVM в разделе 12.1.1. Алгоритм SMO подробно описан в разделе 12.2, который включает в себя решение аналитических шага QP, эвристики для выбора, какие переменные для оптимизации нужны во внутреннем цикле, описание установления порога SVM, и некоторые особые случаи оптимизации. Раздел 12.3 содержит псевдокод алгоритма, а в разделе 12.4 рассматривается взаимосвязь СМО с другими алгоритмами. Раздел 12.5 представляет результаты для отсчета времени SMO против стандартного PCG отрыва алгоритма для различных реальных социальных и Арти наборов данных. Сделаны выводы на основе этих таймингов в разделе 12.6. Два приложения (разделы 12.7 и 12.8) содержат вывод аналитической оптимизации и подробные таблицы SMO против PCG отрывов таймингов.

Для полноты QP проблемы пример SVM показан ниже:

QP проблема в уравнении (12.1) решается с помощью алгоритма SMO. Дело в том, что оптимальная точка (12.1) тогда и только тогда, когда условие окажется выполненным и Q_ij =y_iy_j*k(x_ix_j). Такая точка может быть не уникальной и неизолированно-оптимальной.

12.2 Последовательная минимальная оптимизация

Последовательная Минимальная Оптимизация (SMO) является простым алгоритмом, который быстро решает проблемы SVM QP (quadratic programming – квадратичное программирование) без дополнительного хранения матрицы и без привлечения итерационного численного порядка подготовки для каждой суб-проблемы. SMO раскладывает общую QP проблему в QP подзадачи похоже на метод Osuna.

В отличие от предыдущих способов, SMO выбирает решение наименьшей возможной оптимизации проблемы на каждом шаге. Для стандартной задачи SVM QP, наименьшая возможная задача оптимизации состоит из двух множителей Лагранжа, поскольку мультипликаторы Лагранжа должны подчиняться линейному ограничению равенства. На каждом шаге, SMO выбирает двух множителей Лагранжа совместно оптимизированные оптимальные значения для этих мультипликаторов, и обновляет SVM повторно для новых оптимальных значений.

Преимущество SMO заключается в том, что решение можно сделать аналитически с помощью двух множителей Лагранжа. Таким образом, всю внутреннюю итерацию из-за численной QP оптимизации желательно избегать. Внутренний цикл алгоритма может быть выражен в небольшом количестве С-кода, и для него не нужно запускать всю итерацию QP библиотечной функции. Хотя более оптимизированные суб-проблемы решаются в ходе алгоритма, отдельная суб-проблема находит решение за малое количество итераций, что значительно сказывается на скорости решения проблемы QP.

Кроме того, SMO не требуется дополнительного места для хранения матрицы (не обращая внимания на незначительные количество памяти для хранения любых 2x2 матриц, которое требует SMO). Таким образом, очень большие проблемы SVM обучения могут быть просчитаны внутри памяти обычного персонального компьютера или рабочей станции. Поскольку манипуляции большими матрицами можно избежать, SMO может быть менее чувствительно к числовой проблеме точности. Есть три составляющих SMO: аналитический метод решения для двух множителей Лагранжа, эвристический выбор мультипликаторов для оптимизации, и метод вычисления b.

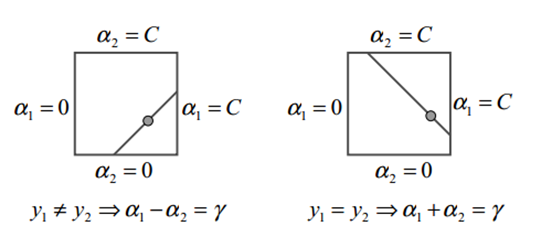
Рисунок 12.2 двух множителей Лагранжа должен содержать все ограничения полной задачи. Ограничения типа неравенства вызывают множители Лагранжа, лежащие в одном квадрате. Линейные ограничения равенства заставляют их выстроится на диагональной линии. В этой фигуре ?= α₁ ^old + s α₂ ^old является константой, которая зависит от предыдущего значения α₁ и α₂ и s = y₁y₂ .

12.2.1 Решение для двух множителей Лагранжа

Для того чтобы решить задачу Лагранжа для двух множителей, SMO RST вычисляет ограничения на эти мультипликаторах, а затем решает для ограниченного максимума. Для удобства все величины, относящиеся к RST мультипликатору будет иметь индекс 1, а все величины, относящиеся ко второму умножителю будет иметь индекс 2. Так как есть только два множителя, ограничения могут быть легко отображается в двух измерениях (см. рисунок 12.2). Это ограничение объясняет, почему минимальное количество множителей Лагранжа равно двум, которые могут быть оптимизированы: если SMO оптимизировал бы только один множитель, он не мог линейного ограничивать равенство на каждом шаге. Концы диагонального отрезка могут быть выражены довольно просто. Без ограничения общности, алгоритм вычисляет RST второй множитель Лагранжа α ₂ и вычисляет концы диагональных отрезков с точки зрения α ₂. Если цель y₁ не равна целевой y₂, то следующие оценки применяются к α ₂.

Если целевая y₁ равна целевой y₂, то следующие оценки относятся к α ₂:

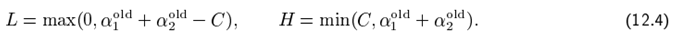
Второй производная наблюдаемой проективной функции вдоль диагональной линии может быть выражена как:

Следующим шагом SMO является вычисление местоположения ограниченного максимума наблюдаемой проективной функции в уравнении (12.1), позволяя изменять только две функции Лагранжа. В нормальных условиях, то будет максимальным вдоль направления линейного ограничения равенства η будет меньше нуля. В этом случае SMO вычисляет максимальный вдоль направления ограничения.

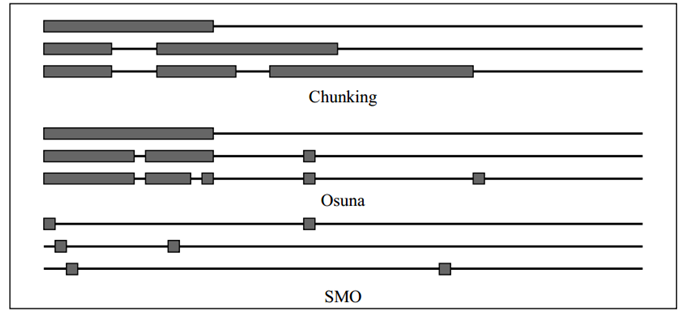
Рисунок 12.1 Три альтернативных метода обучения SVMs: Chunking, алгоритм Osuna, и SMO. Для каждого метода, показано три шага. Горизонтальная тонкая линия на каждом шагу представляет обучающую выборку, а толстые окна представляют собоймножители Лагранжа, которые необходимо оптимизировать на этом шаге. Одной группе из трех линий соответствует три итерации обучения, с первой итерации в верхней части.