Алгоритм A* для новичков.
Автор: Патрик Лестер (Patrick Lester) (2 апреля 2004) Почта:
Перевод: Morpher (26 июля 2004) Почта: Morpher_KKnD@mail.ru
Данная статья переведена на Испанский и Французкий. Другие переводы приветствуются.
Алгоритм A* (произносится как "А-звездочка"), возможно, немного трудноват для новичков. И хотя в сети существует множество материалов, обьясняющих A*, большинство из них написаны для людей, которые уже понимают основы. Эта же статья действительно написана для новичков.
Статья не пытается быть исчерпывающим материалом по данной теме. Вместо этого она описывает фундаментальные понятия и подготавливает вас к тому, чтобы прочитать все те материалы и понять о чем в них идет речь. Ссылки на некоторые из них прилагаются в конце статьи (под заголовком "Дальнейшее изучение").
Также эта статья не направлена на определенный язык программирования - вы сможете адаптировать ее к любому из них. Как вы, должно быть, и ожидали, я добавил ссылку на пример реализации в конце статьи. Архив примера содержит две версии: на C++ и на Blitz Basic. Он также содержит скомпилированную версию, если вы просто хотите увидеть A* в действии.
Но пора приступать к делу. Давайте
начнем с самого начала...
Введение: Область Поиска
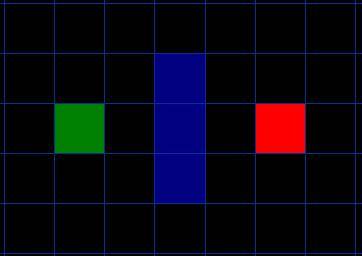
Давайте представим себе, что у нас есть кто-то, кто хочет попасть из точки А в точку B. Эти две точки разделены стеной. На иллюстрации ниже зеленый квадрат это стартовая точка A, красный квадрат - целевая точка B, а несколько синих квадратов - стена между ними.
[Рис. 1]
Первое, на что вы должны обратить внимание, то, что мы разделили нашу область поиска на сетку с квадратными ячейками. Упрощение области поиска это первый шаг в поиске пути. Этот метод упрощает нашу область поиска до простого двумерного массива. Каждый элемент масссива представляет одну из клеток сетки, а его значением будет проходимость этой клетки (проходима и непроходима). Для нахождения пути нам необходимо определить какие нам нужны клетки для перемещения из точки A в точку B. Как только путь будет найден, наш путник начнет двигаться с центра одной клетки на центр следующей до тех пор, пока не достигнет целевой клетки.
Эти центральные точки называют "вершинами". Когда вы что-нибудь читаете про поиск пути, то часто можно столкнуться с обсуждением вершин. Почему бы просто не назвать их клетками? Потому что всегда возможно разделить вашу область поиска на что-то отличное от квадратов. Например, на прямоугольники, шестиугольники, треугольники, или любую другую фигуру. И вершины могут располагаться где-угодно - в центре, вдоль граней или еще где-нибудь. Мы используем эту систему, поскольку она самая простая.
Начало Поиска
Как только мы упростили нашу область
поиска до некоторого числа вершин, нам нужно начать поиск для
нахождения кратчайшего пути. Начнем с точки A, проверяя соседние клетки
и двигаясь дальше до тех пор, пока не найдем целевую точку.
Начинаем поиск пути выполняя следующее:
- Начинаем со стартовой точки A и добавляем ее в "открытый список" клеток, которые нужно обработать. Открытый список это что-то наподобие списка покупок. В данный момент есть только один элемент в списке, но позже мы добавим еще. Список содержит клетки, которые может быть находятся вдоль пути, который вы выберете, а может и нет. Проще говоря, это список клеток, которые нужно проверить.
- Ищем доступные или проходимые клетки, граничащие со стартовой точкой, игнорируя клетки со стенами, водой или другой непроходимой областью. И также добавляем их в открытый список. Для каждой из этих клеток сохраняем точку A, как "родительскую клетку". Эта родительская клетка важна, когда мы будем прослеживать наш путь. Это будет описано намного позже.
- Удаляем стартовую точку A с вашего открытого списка и добавляем ее в "закрытый список" клеток, которые вам больше не нужно проверять.

[Рис. 2]
Дальше мы выберем одну из соседних клеток в открытом списке и практически повторим вышеописанный процесс . Но какую клетку мы выберем? Ту, у которой меньше стоимость F.
Оценка пути
Способом определения того, какую же клетку использовать, является следующие выражение:
F = G + H
где
- G = стоимость передвижения из стартовой точки A к данной клетке, следуя найденному пути к этой клетке.
- H = примерная стоимость передвижения от данной клетки до целевой, то есть точки B. Она обычно является эвристической функцией. Причина по которой она так называется в том, что это предположение. Мы действительно не узнаем длину пути, пока не найдем сам путь, потому что в процессе поиска нам может встретиться множество вещей (например, стены и вода). В этой статье вам предложили один способ вычислить H, но существует множество способов, которые можно найти в других статьях.
Наш путь генерируется путем повторного прохода через открытый список и выбора клетки с наименьшей стоимостью F. Этот процесс будет описан в статье более подробно, но немного позже. Прежде всего давайте внимательно рассмотрим вычисление стоимости F.
Как описано выше, G является стоимостью передвижения со стартовой клетки до текущей, используя найденный к ней путь. В этом примере мы присвоим стоимость 10 к горизонтальным и вертикальным передвижениям, а к диагональным - 14. Мы используем эти числа потому, что пройденное по диагонали расстояние примерно в 1,414 раз (корень с 2) больше стоимости передвижения по горизонтали или вертикали. Для простоты мы используем 10 и 14. Соотношение соблюдается и мы избегаем вычисления квадратных корней и десятичной дроби. Это не просто потому, что мы дураки и не любим математику. Использование целых чисел вроде этих, намного быстрее для компьютера. Как вы скоро узнаете, поиск пути может быть очень медленным если вы не используете упрощения наподобие этих.
Так как мы вычисляем стоимость G вдоль пути к текущей точке, способ ее установить состоит в том, чтобы взять G родительской клетки и прибавить 10 или 14, в зависимости от диагонального или ортогонального (не диагонального) расположения текущей клетки относительно родительской клетки. Необходимость использования этого метода станет очевидной немного позже, когда мы отдалимся от стартовой точки более чем на одну клетку.
Стоимость H может быть вычислена множеством способов. Метод, который мы используем, называется методом Манхеттена (Manhattan method), где вы считаете общее количество клеток, необходимых для достижения целевой точки от текущей, по горизонтали и вертикали, игнорируя диагональные перемещения и любые препятствия, которые могут оказаться на пути. Затем мы умножаем общее количество полученных клеток на 10.
Читая это описание вы, должно быть, решили, что эвристика - просто приблизительное определение оставшегося расстояния между текущей клеткой и целью по прямой. Но это не так. Мы пытаемся установить оставшееся расстояние вдоль пути (который обычно идет не по прямой), но алгоритм требует от нас не переоценить это расстояние, иначе он может найти не верный путь. Использованный здесь метод гарантирует предоставить нам правильный путь. Хотите узнать про эвристику больше? Вы найдете выражения и дополнительные сведенья здесь.
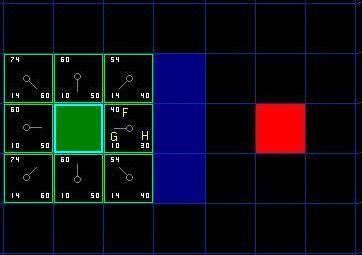
Стоимость F вычисляется путем сложения стоимостей G и H. Результаты первого шага нашого поиска пути проиллюстрированы ниже. Значения F, G и H записаны в каждой клетке. Как видим по клетке справа от стартовой точки, F выводится в верхнем левом углу, G выводится в нижнем левом углу, а H выводится в нижнем правом углу.
[Рис. 3]
Давайте посмотрим на некоторые из этих клеток. В клетке с буквами G = 10. Это потому, что она находится на расстоянии в одну клетку от стартовой точки, при том по горизонтали. Также G = 10 у клеток прямо сверху, снизу и слева от стартовой точки. У диагональных клеток G = 14.
Стоимость H посчитана с помощью вычисления Манхеттенского расстояния к красной целевой клетке, двигаясь только по горизонтали и вертикали, игнорируя все стены на пути. У клетки, прямо справа от стартовой, расстояние до цели 3 клетки. Используя этот метод видим, что H = 30. У клетки прямо над ней, расстояние уже 4 клетки (помните, что надо двигаться только по горизонтали и вертикали). И ее значение стоимости H будет равно 40. Вы, вероятно, можете догаться, как вычисляются стоимости H для других клеток.
Стоимость F для каждой клетки
вычисляется простым суммированием G и H.
Продолжаем поиск
Для продолжения поиска мы просто выбираем клетку с наименьшей стоимостью F из всех клеток, находящихся в открытом списке. Затем с выбранной клеткой мы производим такие действия:4) Удаляем ее из открытого списка и добавляем в закрытый список.
5) Проверяем все соседние клетки. Игнорируем те, которые находятся в закрытом списке или непроходимы (поверхность со стенами, водой), остальные добавляем в открытый список, если они там еще не находятся. Делаем выбранную клетку "родительской" для всех этих клеток.
6) Если соседняя клетка уже находится в открытом
списке, проверяем, а не короче ли путь по этой клетке? Иными словами,
сравниваем значения стоимости G этих двух клеток. Если при
использовании этой клетки стоимость G выше, чем при использовании
текущей клетки, то не предпринимаем ничего.
Если же она ниже, то меням "родителя" этой клетки на выбранную клетку.
Затем вычисляем стоимости F и G этой клетки. Если это выглядит для вас
немного запутанным, далее вы можете увидеть это на иллюстрации.
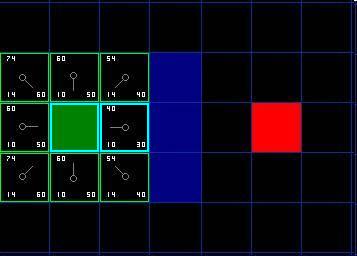
Хорошо, давайте посмотрим, как это работает. С наших начальных 9 клеток, осталось 8 в открытом списке, а стартовая клетка была внесена в закрытый список. Клетка с наименьшей стоимостью F находится прямо справа от стартовой клетки, и ее стоимость F = 40. Поэтому мы выбираем эту клетку как нашу следующую клетку. Она выделена голубым цветом на этой иллюстрации.
[Рис. 4]
Сначала мы удаляем ее из открытого списка и добавляем в закрытый список (вот почему она выделена голубым цветом). Затем мы проверяем соседние клетки. Клетки, сразу справа от этой клетки - стены, поэтому мы их игнорируем. Клетка, прямо слева - стартовая клетка. Она находится в закрытом списке, поэтому мы ее тоже игнорируем.
Оставшиеся 4 клетки уже находятся в открытом списке, поэтому мы должны проверить, не короче ли пути по этим клеткам, используя текущую клетку. Сравнивать будем по соимости G. Давайте посмотрим на клетку, прямо под нашей выбранной клеткой. Ее стоимость G равна 14. Если мы будем двигаться по этой клетке, стоимость G будет равна 20 (10, соимость G чтобы добраться к текущей клетке плюс 10 для движения вертикально вверх, к соседней клетке). Стоимость G = 20 больше, чем G = 14, потому это будет не лучший путь. Это станет понятным, если взглянуть на диаграму. Более целесообразным будет движение по диагонали на одну клетку, чем движение на одну клетку по горизонтали, а потом одну по вертикали.
Когда мы повторим этот процесс для всех 4-х соседних клеток, которые находятся в открытом списке, то узнаем, что ни один из путей не улучшится при движении по этим клеткам через выбранную, потому ничего не меняем. Теперь, когда мы осмотрели все соседние клетки, то закончили с текущей клеткой и готовы двигаться к следующей.
Теперь мы проходим весь открытый список, который уменьшился до 7-ми клеток, и выбираем клетку с наименьшей стоимостью F. Интересно, что в этом случае существует 2 клетки со стоимостью 54. Так какую мы выберем? Это не имеет никакого значения. В целях увеличения скорости поиска можно выбрать последнюю клетку, которую мы добавили в открытый список. Это предупредит поиск в выборе клеток, к которым можно будет обратиться позже, когда мы подберемся ближе к цели. Но в действительности это не так уж важно. (Вот почему две версии A* могут найти разные пути с одинаковой длиной.)
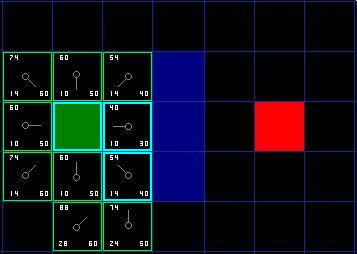
Так что давайте выберем клетку, прямо внизу, спава от стартовой, как показано на рисунке.
[Figure 5]
В этот раз, когда мы проверяем соседние клетки, видим, что клетка, прямо справа - стена и мы ее пропускаем. Так же поступаем и с клеткой, которая находится прямо над ней. Так же мы игнорируем клетку, которая находится прямо под ней. Почему? Потому, что вы не можете добраться до той клетки без среза угла ближайшей стены. Сначала вы должны спуститься вниз, а только потом двигаться на эту клетку. (Замечание: Это правило среза углов необязательно. Его использование зависит от расположения ваших вершин.)
Остается еще 5 клеток. 2 клетки, находящиеся под текущей, еще не в открытом списке, потому мы их добавляем в открытый список и назначаем текущую клетку их "родителем". Из 3-х других клеток 2 уже находятся в закрытом списке (стартовая клетка и клетка, прямо над ней, на диаграмме обе подсвечены голубым цветом) и мы их игнорируем. Последняя клетка, которая находится прямо слева от текущей, проверяется на длину пути по текущей клетке через эту клетку по стоимости G. Нет, путь будет не короче. Так что мы здесь закончили и готовы проверить следующую клетку в открытом списке.
Повторяем этот процесс до
тех пор, пока не добавим целевую клетку в открытый список. К этому
времени у вас получится что-то похожее на иллюстрацию ниже.
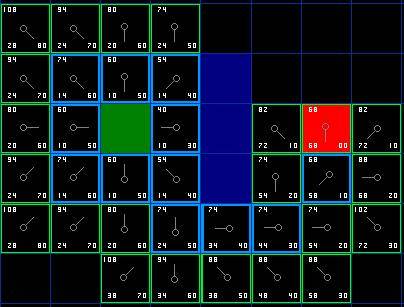
[Рис. 6]
Заметьте, что родительская клетка для клетки,
находящейся в 2-х клетках под стартовой изменилась по сравнению с
предидущей иллюстрацией. Преред этим у нее стоимость G была равна 28 и
указатель был направлен вверх и влево. Теперь стоимость G равна 20, а
указатель направлен прямо вверх. Это произошло где-то в процессе нашего
поиска, когда была проверена стоимость G и оказалось, что путь через
эту клетку будет более коротким. Поэтому поменялась ее родительская
клетка и были пересчитаны стоимости G и F. И хотя в этом примере это не
кажется очень важным, существует множестиво ситуаций, когда такая
проверка
будет сильно влиять на выбор более короткого пути к цели.
Так как же мы определим сам путь? Очень просто. Начнем с красной целевой клетки и будем двигаться назад с клетки на ее родителя, следуя указателям. Это доставит вас к стартовой клетке и это и будет ваш путь. Получится как показано на иллюстрации ниже. Движение от стартовой точки A к целевой точке B будет просто передвижением от центра каждой клетки (вершины) к центру следующей клетки до тех пор, пока вы не достигните цели.
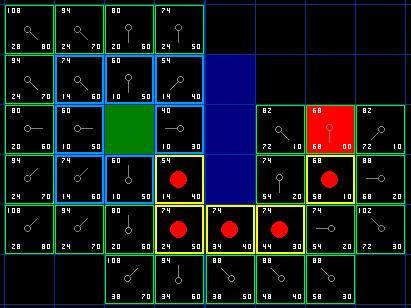
[Рис. 7]
Итоги метода A*
Хорошо, вы прошли все обьяснение, давайте посмотрим на пошаговое представление этого метода:1) Добавляем стартовую клетку в открытый список.
2) Повторяем следующее:
a) Ищем в открытом списке клетку с наименьшей стоимостью F. Делаем ее текущей клеткой.
b) Помещаем ее в закрытый список. (И удаляем с открытого)
c) Для каждой из соседних 8-ми клеток ...
-
Если клетка непроходимая или она находится в закрытом списке, игнорируем ее. В противном случае делаем следующее.
-
Если клетка еще не в открытом списке, то добавляем ее туда. Делаем текущую клетку родительской для это клетки. Расчитываем стоимости F, G и H клетки.
-
Если клетка уже в открытом списке, то проверяем, не дешевле ли будет путь через эту клетку. Для сравнения используем стоимость G. Более низкая стоимость G указывает на то, что путь будет дешевле. Эсли это так, то меняем родителя клетки на текущую клетку и пересчитываем для нее стоимости G и F. Если вы сортируете открытый список по стоимости F, то вам надо отсортировать свесь список в соответствии с изменениями.
d) Останавливаемся если:
- Добавили целевую клетку в открытый список, в этом случае путь найден.
- Или открытый список пуст и мы не дошли до целевой клетки. В этом случае путь отсутствует.
3) Сохраняем путь. Двигаясь назад от целевой точки, проходя от каждой точки к ее родителю до тех пор, пока не дойдем до стартовой точки. Это и будет наш путь.
Послесловие
Для ипользования алгоритма A*, вам необходимо включить элементы, описанные выше -- открытый и закрытый списки, стоимости F, G, и H. Существует множество других алгоритмов поиска пути, но эти методы не A*, который считается лучшим из многих. Брайан Стаут (Bryan Stout) обсуждает многие из них в статье, ссылка на которую расположена чуть дальше. Некоторые альтернативные методы будут лучше при некотрых обстоятельствах, но вы должны понимать, что вам надо. Ладно, хватит разглагольствований. Вернемся к нашей статье.
Заметки к реализации
Теперь, когда вы понимаете основы метода, вот несколько
тем к размышлению, когда вы начнете писать свою программу. Некоторые из
этих материалов ссылаются на программу, которую я написал на C++ и
Blitz Basic, но это будет актуально и для других языков.
1. Другие юниты (уклонение
от столкновений) Если вы
присмотритесь внимательней к моему примеру реализации алгоритма, вы
заметите, что он полностью игнорирует все остальные юниты на экране.
Юниты спокойно проходят сквозь друг друга. В зависимости от игры, это
может быть приемлимым, но может и не быть. Если вы хотите чтобы юниты
обходили друг друга, то я предлагаю вам несколько методов. Можно
обратбатывать юниты, которые не двигаються или находятся близко к
юниту, для которого ищется путь, а остальные просто игнорировать. Если
же вы хотите обрбатывать юниты, которые двигаются и находятся на
расстоянии более чем в одну вершину, то вам нужно будет разработать
метод для установления их положения в пространстве в любое время, чтобы
они могли должным образом уклониться. Иначе в дальнейшем вы можете
столкнуться со странными путями, где юниты двигаються по
зигзагообразной траектории, пытаясь обьехать другие юниты, которых там
давно нет. Вам также потребуется система определения столкновений, так
как не важно насколько хорош ваш путь, со временем многие вещи могут
измениться. Когда происходит столкновение, для юнита надо просчитать
новый путь или, если это не лобовое столкновение, подождать пока другой
юнит отойдет с дороги, перед тем, как двигаться дальше.
Вот некоторые ссылки, которые могут вам
пригодиться:
- Steering Behavior for Autonomous Characters: по движению автономных устройств немного отходит от задачи поиска пути, но она может быть интегрирована с ним для более совершенного перемещения и определения столкновений.
- The Long and Short of Steering in Computer Games: Интересный обзор литературы по передвижению и поиску пути. Это pdf документ.
- Coordinated
Unit Movement: Первая статья из двухсерийного цикла про формацию и
сгруппированое передвижение юнитов от дизайнера Эпохи Империй (Age of
Empires) Дейва Поттингера (Dave Pottinger).
- Implementing Coordinated Movement: Вторая статья из этого цикла.
2. Различная стоимость передвижения: В этой статье и в моей прилагающейся программе поверхность может быть только двух типов - проходимая и непроходимая. Но что, если у вас есть территория, которая проходимая, но имеет большую стоимость передвижения? Болота, возвышенности, лестницы в пещерах, и т.д. - это примеры поверхности, котрую можно пройти, но стоимость передвижения у нее выше, чем стоимость передвижения по ровной, открытой поверхности. Также стоимость передвижения по дорогам может быть немного ниже стоимости передвижения по другим видам поверхности.
Эта проблема легко решается путем добавления стоимости поверхности при вычислении стоимости G любой вершины. Просто добавьте дополнительную стоимость к таким вершинам. Алгоритм поиска пути A* написан для нахождения пути с наименьшей стоимостью и легко справится с такой задачей. В простом примере, который я описал, когда поверхность может быть или проходимой или нет, A* будет искать кратчайший, более прямолинейный путь. Но в случае с различной стоимостью поверхности, юнит может пойти более длинным путем - как, например, при движении по дороге через болото, а не движении напрямик по самому болоту.
Существует еще одно интересное решение, которое проффесионалы называют "influence mapping" (что-то вроде карты с областями влияния). Так же как и с различной стоимостью поверхности, вы можете создавать дополнительные системы и применять их для целей ИИ (искуственного интеллекта). Представьте, что у вас есть карта, на которой находятся толпы юнитов, охраняющих проезд через горный регион. Каждый раз, когда компьютер посылает свой юнит через этот проход, он уничтожается. Если вы захотите, то можете создать "карту влияний", которая будет "штрафовать" вершины, возле которых множество вражеских единиц. Это научит компьютер планировать более безопасные пути и поможет избежать глупых ситуаций, когда компьютер продолжит посылать юниты через более опасный район только потому, что он более короткий.
3. Обработка неизведанных территорий: Вы когда-нибудь играли в игры, в которых компьютер всегда знает точно какой путь выбрать, даже если карта еще не полностью исследована? В зависимости от игры, поиск пути это то, что может быть очень нереалистичным. К сожалению, это та проблема, которую не так-то просто решить.
Ответ заключается в создании массива "известнаяПроходимость" для каждого из игроков и компьютерных оппонентов ("каждый игрок" не значит "каждый юнит", это потребовало бы очень много памяти). Каждый такой массив должен содержать информацию про области, которые игрок уже исследовал, остальные же области должны оставаться непроходимыми до исследования. Используя такое решение, юниты будут попадать в тупики и искать неверный путь до тех пор, пока они не откроют всю карту. Как только карта будет исследована, поиск пути станет всегда находить верные пути.
4. Сглаженные пути: A* даст вам кратчайший, с наименьшей стоимостью путь, но он не даст вам визуально сглаженного пути. Давайте посмотрим на окончательный путь, просчитанный в примере (рис. 7). На этом пути первый шаг находится справа внизу от стартовой клетки. Не казался бы наш путь более плавным, если бы первый шаг находился прямо под стартовой клеткой?
Есть несколько способов решить эту проблему. В процессе поиска вы можете "штрафовать" вершины, где есть смена направления движения, увеличивая их стоимости G. Так же вы можете пройти по всему пути после его вычисления и выискивать вершины, в которых вы бы хотели изменить направление для более сглаженного пути. Для более обширного описания проблемы, проверьте , Toward More Realistic Pathfinding, бесплатную (но требующую регистрации) статью Марка Пинтера (Marco Pinter) на Gamasutra.com.
5. Неквадратные области поиска: В нашем примере мы используем простые плоские квадратные ячейки. Необязательно всегда выбирать такое решение. Вы можете использовать области с неправильной формой. Вспомните про игру Risk (Риск :-) и страны в ней. Вы можете захоть использовать такой сценарий поиска пути. Для того, чтобы это сделать вам необходимо создать таблицу для хранения информации о том, какие страны с какими граничат и стоимости G для передвижения от одной страны к другой. Вы также должны выбрать метод определения стоимости H. Все остальное остается таки же, как и в нашем примере. При добавлении элементов в открытый список, вместо просмотра соседних клеток просто просматривайте соседние страны в таблице.
Также вы можете создать систему вэйпоинтов для путей нафиксированной карте. Вэйпоинты представляют собой несколько связанных точек пути, например, на дороге или в тунелле подземелья. Как гейм-дизайнер вы можете указывать эти вэйпоинты вручную. Два вэйпоинта считаются соседними, если на линии между ними нет никаких препятствий. В случае с игрой Риск (Risk), вы сохраняете эту информацию о соседстве в какой-нибудь таблице и используете эту информацию при генерации элементов открытого списка. Затем вы сохраняеете присвоенные стоимости G (возможно, используя длины отрезков, соеденяющих вершины) и стоимости H (возможно, используя длины отрезков, соеденяющих вершины и цель). Все остальное выполняется как обычно.
Амит Пател (Amit Patel) написал статью предлагающую некоторые альтернативы. Пример по поиску на изометрической RPG карте, используя неквадратные области поиска, лежит здесь: Two-Tiered A* Pathfinding.6. Некоторые советы по увеличению скорости поиска: Как только вы разработаете свою собственную программу A*, или адаптируете ту, которую написал я, то обнаружите, что поиск пути использует львиную долю вашего процессорного времени, особенно если у вас огромное количесво юнитов и большая карта. Если вы прочитаете в сети различные материалы, то узнаете, что это распостраняется даже на программистов таких игр, как Starcraft или Age of Empires. Если вы заметили, что поиск пути стал медленным, то вот несколько советов о том, как ускорить этот процесс:
- Используйте карты поменьше и небольшое количество юнитов.
- Никогда не ищите путь одновременно для нескольких юнитов. Вместо этого поставьте их в очередь и рассчитывайте за несколько игровых циклов. Если ваша игра работает на скорости, скажем, в 40 циклов за кадр, никто никогда этого не заметит. Но все заметят, если игра начнет работать очень медленно каждый раз, когда путь вычисляется одновременно для множества юнитов.
- Используйте для вашей карты как можно большие квадраты (или любую другую фигуру). Это уменьшит общее количество вершин просмотренных при поиске пути. Если вы очень амбитный человек, то можете использовать две или больше систем поиска пути, которые будут использоваться в разных ситуациях в зависимости от длины пути. Вот что делают проффесионалы: используют большие области для длинных путей, а затем переходят на более точный поиск, используя меньшие квадраты/области при приближении к цели. Если вы заинтересованы в таком подходе, прочтите мою статью Two-Tiered A* Pathfinding.
- Для длинных путей можно использовать предварительно просчитанные пути.
- Обрабатывайте вашу карту на наличие недоступных из других частей карты участков. Я называю эти участки "острова." В действительности они могут быть островами или любой другой поверхностью, которая отгорожена стенами или недоступна. Один из недостатков алгоритма A* состоит в том, для нахождения путей к таким участкам, он будет искать путь на всей карте, останавливаясь только когда каждый квадрат/вершина прошли через открытый и закрытый списки. Это может потратить очень много процессорного времени. Этого можно избежать если просчитывать какие области недостижими (с помощью flood-fill заливки или похожего метода), сохраняя эту информацию в любом массиве и проверяя ее каждый раз перед началом поиска.
- В запутанном, лабиринтоподобном окружении, стоит отметить вершины, которые не приводят никуда, кроме тупиков. Такие области можно указывать на вашей карте вручную или, если вы очень амбитны, разработать алгоритм, который будет опряделять такие области автоматически. Любой группе таких вершин можно присвоить уникальный идентификационный номер. Затем вы можете спокойно игнорировать все тупики при поиске пути, задумывая сь только о том, чтобы стартовая или челевая точки не попали в такую "тупиковую" область.
7.
Реализация открытого списка: Это
один из наиболее важных элементов в алгоритме A*. Каждый раз при
обращении к открытому списку вам необходимо найти вершину с наименьшей
стоимостью F. Существует несколько способов это сделать. Вы можете
сохранять элементы пути когда потребуется и просто проматривать весь
открытый список каждый раз, когда надо извлечь элемент с наименьшей
стоимостью F. Это простой метод, но очень медленный для длинных путей.
Он может быть улучшен использованием сортированного списка и тогда
нуждно будет просто выбрать первый элемент списка - это и будет элемент
с наименьшей стоимостью F. Когда я писал свою программу этот метод был
первым, который я использовал.
Это будет быстро работать на маленьких картах,
но это не оптимальное решение. Серьезные программисты A*, которые
стремятся действительно к впечатляющей скорости, используют что-то, что
называются "двоичными кучами" (binary heaps) и это то, что я
использовал в своей программе. Это будет по крайней мере в 2-3 раза
быстрее в большинстве случаев и намного быстрее (в 10 и больше раз) на
длинных путях. Если вы заинтересовались, прочтите мою статью Using
Binary Heaps in A* Pathfinding.
8. Алгоритм Дийкстры: В
то время, как считается, что A* самый лучший алгоритм поиска (смотрите
выше), сущетвует по крайней мере еще один алгоритм, который активно
используется - алгоритм Дийкстры (Dijkstra's algorithm). Этот алгоритм
точно такой же как и A*, только без эвристики (H всегда равна 0). Так
как в нем нет эвристики, он ищет путь одновременно во все стороны.
Перед тем, как найти путь, алгоритм исследует намного больше
территории. Это делает его медленнее A*.
Так зачем его использовать? Иногда мы не знаем где находится наша цель. Например, у вас есть добывающий юнит, которому надо собрать каких-нибудь ресурсов. Он может знать, что на этой территории есть несколько областей с ресурсами, но он хочет добраться к ближайшим. Здесь использовать алгоритм Дийкстры будет более целесообразно, чем использовать A* потому, что мы не знаем, какие из ресурсов находятся ближе. Альтернатива есть только в повторном использовании A* для нахождения расстояния до каждого из ресурсов, а затем использовании этого пути. Существует множество таких ситуаций.
Дальнейшее изучение
Хорошо, теперь вы знаете основы и смысл некоторых углубленных решений. На этом этапе я советую заглянуть в мой исходный код. Архив содержит две версии: на C++ и на Blitz Basic. Обе версии содержат множество комментариев и должны быть довольно простыми в пониманииd. Вот ссылка.
Если у вас нет возможности работать на C++ или в Blitz Basic, два небольших exe-файла находятся в папке с версией на C++. Версия на Blitz Basic может быть скомпилирована с помощью бесплатной демо-версии Blitz Basic 3D (не Blitz Plus) на оффициальном сайте Blitz Basic. Сетевая демонстрация Бена О'Нилла (Ben O'Neill) находится тут.
Вы также можете заинтересоваться некоторыми сайтами. После прочтения этой статьи они будут простыми для понимания.
- Amit’s A* Pages: Это очень обширная страничка Амита Патела (Amit Patel), но она может быть немного непонятной для тех, кто не читал эту статью. Но все же стоит глянуть. Советую прочитать личные рассуждения Амита про статью.
- Smart Moves: Intelligent Path Finding: Эта статья написана Брайаном Стаутом (Bryan Stout) для портала Gamasutra.com и требует регистрации для чтения. Регистраци бесплатна и позволяет прочитать не только эту статью но и множество других ресурсов, дуступных на сайте. Программа, написанная Брайаном на Delphi помогла мне изучить A* и вдохновила на написание моей программы A*. Также она описывает некоторые альтернативные возможности A*.
- Terrain Analysis: Это сложная, но интересная статья Дейва Поттингера (Dave Pottinger), проффесионала из Ensemble Studios. Этот парень координировал разработку Эпохи Империй (Age of Empires) и ее второй части. Не ожидайте, что вы поймете все, написанное в ней, но это очень интересная статья, которая может натолкнуть вас на некоторые идеи. Она включает в себя обсуждение мип-маппинга, карты с влияниями и некоторыми другими углубленными решениями ИИ/поиска пути. Обсуждение "заливки" (“flood filling”) послужило идеей моих собственных "тупиков"и "островов"(“dead ends” and “islands”) , которые прилагаются к Blitz версии моей программы..
Вот некоторые интересные сайты, которые следует просмотреть: