Реферат по теме выпускной работы

Содержание

1. Введение
2. Цели и задачи работы
3. Мотивация
4. Обзор исследований и разработок
   1. Локальный обзор
   2. Глобальный обзор
5. Краткое изложение собственных результатов
6. Заключение
7. Список источников

Введение

За короткое время своего существования 3D-графика нашла свое применение в самых разных областях: разработка компьютерных игр, медицина, проектирование, дизайн и многие другие сферы [1].

Одним из направлений использования 3D-графики в медицине является создание 3D-моделей органов, суставов, клеток и др. Трехмерное моделирование позволяет также создавать видеоролики на медицинскую тематику [1].

Часто используют трехмерную графику для демонстрации всевозможных физиологических процессов, таких как движение крови по сосудам, формирование холестериновых бляшек, размножение вирусов и т.д. Таким образом, можно в динамике увидеть многие процессы, которые раньше могли наблюдать только по статическим изображениям [1].

Цели и задачи работы

Целью работы является разработка специализированной компьютерной системы (СКС), которая будет строить приближенную трехмерную модель клетки крови человека нейтрофила в процессе прикрепления.

Для выполнения поставленной цели необходимо выполнить ряд задач:

1. Детальное изучение предмета исследования и предыдущих разработок.
2. Изучение принципов и выбор методов построения 3d моделей.
3. Обзор и выбор технологий, сред и соответствующего языка программирования для реализации компьютерной системы.
4. Разработать математический аппарат, основанный на инструментах аналитической геометрии для расчета всех необходимых геометрических параметров нейтрофила в процессе прикрепления в различные моменты времени.
5. Провести выбор существующих математических решений для дополнительных вычислений с целью определения численных параметров необходимых при построении 3d модели.
6. Разработать СКС, выполняющую расчет требующихся данных, трехмерную визуализацию, проекции состояний нейтрофила в разные моменты времени, графическое отображение динамики процесса прикрепления.
7. Проанализировать точность полученных результатов моделирования и на их основании сделать вывод о разработанной СКС.

Мотивация

Одной из задач в практической медицине и цитологии есть отслеживание изменений параметров клеток во время какого-либо процесса их жизнедеятельности. Это позволяет в некоторой мере сделать вывод о степени полноценности их функционирования.

Научные данные часто бывают сложными, и соотношения между различными переменными в эксперименте иногда трудно представить зрительно. Графика является средством для представления научной информации в форме, обеспечивающей наглядное восприятие. Когда данные представлены должным образом, суть исследуемого процесса нередко понимается по-новому [2].

В данной работе идет отслеживание изменений параметров нейтрофилов по истечению определенных промежутков времени. Изучение таких изменений с использованием микроскопа очень затруднительно и поэтому требует дополнительной помощи вычислительной техники.

В процессе наблюдения за объектом под микроскопом можно рассмотреть его только с одной стороны и в настоящий момент времени. Для того, чтобы рассмотреть как изменилась форма и вид объекта через некоторое время или вконце выполнения им какого-либо процесса, необходимо ждать час, два, а то и более, что очень тормозит процесс наблюдения за объектом и его изучение. Кроме того под микроскопом не всегда можно рассмотреть интересующие области со всех сторон. Поэтому, в данной работе строится модель нейтрофила с целью экономии времени в процессе наблюдения за этими клетками, а именно визуализируются в трехмерном виде геометрические изменения нейтрофила в различные моменты времени.

Обзор исследований и разработок

Поскольку исследование динамики процесса прикрепления нейтрофилов детально проводилось в НИИ Медицинских Проблем Семьи, то обзор всего материала, который касается темы прикрепления нейтрофилов, будет только локальный, а глобальный обзор будет направлен на рассмотрение методов трехмерного моделирования.

Локальный обзор

В НИИ Медицинских Проблем Семьи проводили исследование нейтрофилов. Исследовали 8 нейтрофилов в 4-х образцах гепаринизированной (5 мкл/мл) капиллярной крови в процессе их фагоцитоза при комнатной температуре. Кровь брали у здоровых добровольцев (4 мужчин, 1 женщина, возраст 19-20 лет). Объектом фагоцитоза служили бактерии, попавшие естественным образом из внешней среды в кровь после ее забора. Оцифрованные изображения проекций нейтрофилов на плоскость получали путем микроскопирования под иммерсией. Использовали микроскоп ЛЮМАМ-Р3 («ЛОМО») с объективом х90, цифровую видеокамеру CCD Oscar Color Camera OS-35II ("SCAR") и программу для захвата, хранения и просмотра изображений ASUS Live Version 4.6 B2 [3].

На изображениях с помощью специальной компьютерной программы выделяли контур проекции нейтрофила на плоскость, как показано на рис. 1, измеряли периметр (P) и площадь (S) и рассчитывали компактность (C = P2/4πS) – морфометрические показатели (М). Параметры кинетической уравнений находили с помощью пакета статистических программ R for Windows FAQ Version for R-2.4.1. Для каждой клетки находили 10 контуров и рассчитывали средние значения с доверительной вероятностью 0,95. Относительный доверительный интервал расчетных значений P и S не превышал ± 10 % [4].

Рисунок 1 – Изображения неоконтуренного и оконтуренного нейтрофила

В работе [5] были выведены кинетические уравнения, описывающие процесс прикрепления нейтрофилов крови человека. Найдены параметры уравнения и рассчитано время завершения процесса прикрепления. Изменения морфометрических параметров от времени могут описываться уравнением первого порядка:

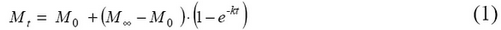
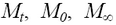где – P или S при 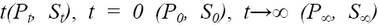, соответствено, k – константа скорости первого порядка, .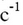

Зависимость также может быть описана другим кинетическим уравнением второго порядка, аналогичным первому [3]:

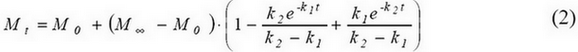
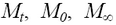где – P или S при 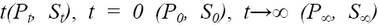, соответствено, 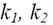– константы скорости первого и второго порядка, .

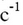В работе Фомичёва К.А., Герасимова И.Г обсуждается моделирование процессов жизнедеятельности клеток: прикрепление, фагоцитоз, трансформация, пролиферация, некроз, апоптоз [6]. Разработана схема специализированной компьютерной системы для моделирования процессов прикрепления, фагоцитоза, трансформацию, пролиферации, апоптоза и некроза клетки и отображения данных процессов жизнедеятельности клетки постепенно от начала до конца. Моделирование позволяет указывать исходные геометрические параметры клетки, а также параметры внешней среды, которые влияют на скорость процесса [6].

В последней работе Фомичёва К.А., Герасимова И.Г обсуждается моделирование изменений морфометрических параметров клеток в процессе прикрепления. В результате вычислений и работы программы выводится статистика изменений параметров клетки в процессе прикрепления. Статистика имеет вид графика, который можно масштабировать и отслеживать значения параметров [7].

Глобальный обзор

Типы 3d моделей:

Граничные модели:
• представление в виде набора вершин, ребер и плоских многоугольников (полигональных сеток)
• представление с использованием параметрических бикубических порций (кусков)
Иерархические
Гибридные

Полигональные сетки

Полигональная сетка представляет собой совокупность ребер, вершин и многоугольников. Вершины соединяются ребрами, а многоугольники рассматриваются как последовательности ребер или вершин. Сетку можно представить несколькими различными способами, каждый из них имеет свои достоинства и недостатки. Для оценки оптимальности представления используют следующие критерии [8]:

• Объем требуемой памяти;
• Простота идентификации ребер, инцидентных вершине;
• Простота идентификации многоугольников, которым принадлежит данное ребро;
• Простота процедуры поиска вершин, образующих ребро;
• Легкость определения всех ребер, образующих многоугольник;
• Простота получения изображения полигональной сетки;
• Простота обнаружения ошибок в представлении (например, отсутствие ребра или вершины или многоугольника) [8].

Явное задание многоугольников

Каждый многоугольник можно представить в виде списка координат его вершин [8]:

Вершины запоминаются в том порядке, в котором они встречаются при обходе вокруг многоугольника. При этом все последовательные вершины многоугольника (а также первая и последняя) соединяются ребрами. Для каждого отдельного многоугольника данный способ записи является эффективным, однако для полигональной сетки дает потери памяти вследствие дублирования информации о координатах общих вершин [8].

Полигональная сетка изображается путем вычерчивания ребер каждого многоугольника, однако это приводит к тому, что общие ребра рисуются дважды – по одному разу для каждого из многоугольников [8].

Задание многоугольников с помощью указателей в список вершин

При использовании этого представления каждый узел полигональной сетки запоминается лишь один раз в списке вершин V =((x1, y1, z1), … , (xn, yn, zn)). Многоугольник определяется списком указателей (или индексов) в списке вершин. Многоугольник, составленный из вершин 3, 5, 7 и 10 этого списка, представляется как Р = (3, 5, 7, 10) [8].

Такое представление имеет ряд преимуществ по сравнению с явным заданием многоугольников. Поскольку каждая вершина многоугольника запоминается только один раз, удается сэкономить значительный объем памяти. Кроме того, координаты вершины можно легко изменять. Однако все еще не просто отыскивать многоугольники с общими ребрами. Ребра при изображении всей полигональной фигуры по-прежнему рисуются дважды. Эти две проблемы можно решить, если описывать ребра в явном виде [8].

Явное задание ребер

В этом представлении имеется список вершин V, однако теперь рассматривается многоугольник как совокупность указателей на элементы списка ребер, в котором ребра встречаются лишь один раз. Каждое ребро в списке ребер указывает на две вершины в списке вершин, определяющие это ребро, а также на один или два многоугольника, которым это ребро принадлежит. Таким образом, мы описываем многоугольник как P =(E1, ..., E2), а ребро – как Е = (V1, V2, P1, P2). Если ребро принадлежит только одному многоугольнику, то либо P1 либо P2 – пусто [8].

При явном задании ребер полигональная сетка изображается путем вычерчивания не всех многоугольников, а всех ребер. В результате удается избежать многократного рисования общих ребер. Отдельные многоугольники при этом также изображаются довольно просто [8].

Равномерная сетка

Эта модель описывает координаты отдельных точек поверхности следующим способом. Каждому узлу сетки с индексами (i, j) приписывается значение высоты zij. Индексам (i, j) отвечают определенные значения координат (x, y). Расстояние между узлами одинаковое – dx по оси x, dy по оси y. Фактически такая модель – это двумерный массив, растр, матрица, каждый элемент которой сохраняет значение высоты. Не каждая поверхность может быть представлена этой моделью. Если в каждом узле (i, j) записывается только одно значение высоты, то это означает, что поверхность описывается однозначной функцией z = f (x, y). Иначе говоря, это такая поверхность, которую каждая вертикаль пересекает только один раз. Не могут моделироваться также вертикальные грани. Необходимо заметить, что сетка может быть задана не только в декартовых координатах. Например, для того чтобы описать поверхность шара однозначной функцией, можно использовать полярные координаты [9].

Неравномерная сетка

Неравномерной сеткой называется модель описания поверхности в виде множества отдельных точек {(x0, y0, z0), (x1, y1, z1), …,(xn-1, yn-1, zn-1)}, принадлежащих поверхности. Такую модель можно считать обобщением для некоторых рассмотренных выше моделей. Например, векторная полигональная модель и равномерная сетка могут считаться разновидностями неравномерной сетки [9].

Неравномерность задания опорных точек усложняет определение координат для других точек поверхности, которые не совпадают с опорными точками. Требуются специальные методы пространственной интерполяции [9].

Пусть задача заключается в вычислении значения координаты z по известным координатам (x, y). Для этого необходимо найти несколько самых близких точек, а затем вычислить искомое значение z, исходя из взаимного расположения этих точек в проекции (x, y). Для равномерной сетки эта задача решается достаточно просто – поиска фактически нет, сразу рассчитываются индексы самых близких опорных точек [9].

Вторая задача заключается в отображении (визуализации) поверхности. Эту задачу можно решать несколькими способами. Один из наиболее распространенных – триангуляция. Процесс триангуляции может быть представлен следующим образом [9]:

• Находим первые три самые близкие друг к другу точки – получаем одну плоскую треугольную грань;
• Находим точку, ближайшую к этой грани, и образовываем смежную грань, и т.д., пока не останется ни одной отдельной точки.

Это – общая схема триангуляции. В литературе можно встретить множество алгоритмов триангуляции, сводящихся к описаному выше. Один из наиболее распространенных – триангуляция Делоне [9].

Описание поверхности треугольными гранями можно уже считать разновидностью векторной полигональной модели. В англоязычной литературе для ее названия используется аббревиатура TIN (Triangulated Irregular Network). После триангуляции получаем полигональную поверхность, отображение которой выполнить уже достаточно просто [9].

Краткое изложение собственных результатов

На данном этапе работы написана программа для расчета и визуализации изменений геометрических параметров клетки крови в процессе прикрепления к субстрату. Разработан определенный математический аппарат для расчета высоты клетки в необходимые моменты времени.

Моделируемая клетка представляется в виде шара, который в процессе прикрепления и контакта с субстратом деформируется. Деформация происходит следующим образом: в начальный момент прикрепления клетка принимает форму полушара, в последующие временные моменты и до окончания прикрепления клетка распластывается и представляет собой сжимающийся полуэллипсоид, в основании которого лежит окружность. Таким образом, видом спереди клетки является полуэллипс, а видом сверху – окружность. Основания эллипса и радиус окружности изменяются с течением времени. В отличие от формы, объем клеток напротяжении всего процесса прикрепления не меняется. Формула площади круга используется для расчета радиуса клетки по морфометрическому параметру – площадь:

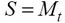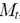, где рассчитывается по уравнениям (1) или (2). Таким образом, радиус клетки в момент времени t:

Если расчет ведется по морфометрическому параметру – периметр, то для вычисления радиуса клетки необходима формула длины окружности:

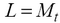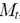, где рассчитывается по уравнениям (1) или (2), таким образом, радиус клетки в момент времени t равен:

Объем полуэллипсоида:

где a, b, c полуоси эллипсоида: c – высота, a, b – большая и малая полуоси эллипса, который лежит в основании. В начальный момент прикрепления t0=0 клетка, как упоминалось выше, представляется половиной шара с радиусом R0. В сечении полушара находится полуэллипс с полуосями a0, с0, при этом a0=с0=R0, а в основании окружность с радиусом R0=a0=b0. Тогда, исходя из формулы (7), объем клетки в начальный момент прикрепления t0 равен:

В следующий момент времени t1 клетка начинает распластываться, контактируя с субстратом, тем самым изменяются значения высоты и радиуса, которые будут равны c1 и R1 соответственно. Тогда объем клетки в момент t1:

Так как объем неизменен напротяжении всего процесса прикрепления, то приравняв правые части уравнений (8) и (9), можно выразить высоту c1 в момент времени t1:

где R0 и R1 рассчитываются по формулам (4) или (6). Высота, полученная по формуле (10) является начальным значением для расчета высот клетки в следующие моменты времени: где i=1,…,n, n – количество временных отсчетов.

По найденным значениям радиуса и высоты рассчитываются точки (xi,yi) для построения видов сверху и спереди:

где a, b – радиус и высота клетки, t – параметр уравнений,

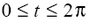
В программе производятся вычисления радиуса и высоты клетки крови в соответствии с ее морфометрическими параметрами. Выполнен расчет точек для построения видов клетки спереди и сверху.

Для разработки компьютерной системы входными данными являются начальные (до прикрепления) и конечные (после завершения прикрепления) морфометрические параметры клетки крови, а также константы скорости для уравнений первого и второго порядков [7].

Разработанная программа – Windows Presentation Foundation (WPF) приложение, для написания которого использовалась среда разработки MS Visual Studio и язык C#.

Была выбрана именно платформа WPF, так как она обладает следующими преимуществами:

1. Независимость от разрешения экрана – поскольку в WPF все элементы измеряются в независимых от устройства единицах, приложения на WPF легко масштабируются под разные экраны с разным разрешением.
2. Новые возможности, которых сложно было достичь в WinForms, например, создание трехмерных моделей, привязка данных и др.
3. Декларативное программирование – некоторая схожесть с языками разметки html/xml, представляя альтернативу программному созданию графики и контролов.
4. Хорошее взаимодействие с WinForms, благодаря чему, например, в приложениях WPF можно использовать традиционные контролы из WinForms [11].

Продемонстрировать результаты работы программы можно приведя некоторые численные данные, которые получились при ее работе, например, в моменты времени t=0 c, t=100 c, t=300 c, t=550 c, t=1500 c и виды клетки сверху и спереди которые изображены на рис. 2. Значения радиуса а и высоты с в эти моменты времени равны:

а=6.3662 мкм, с=6.3662 мкм;
а=6.57 мкм, с=5.9763 мкм;
а=6.8863 мкм, с=5.4389 мкм;
а=7.1534 мкм, с=5.0413 мкм;
а=7.5472 мкм, с=4.5295 мкм.

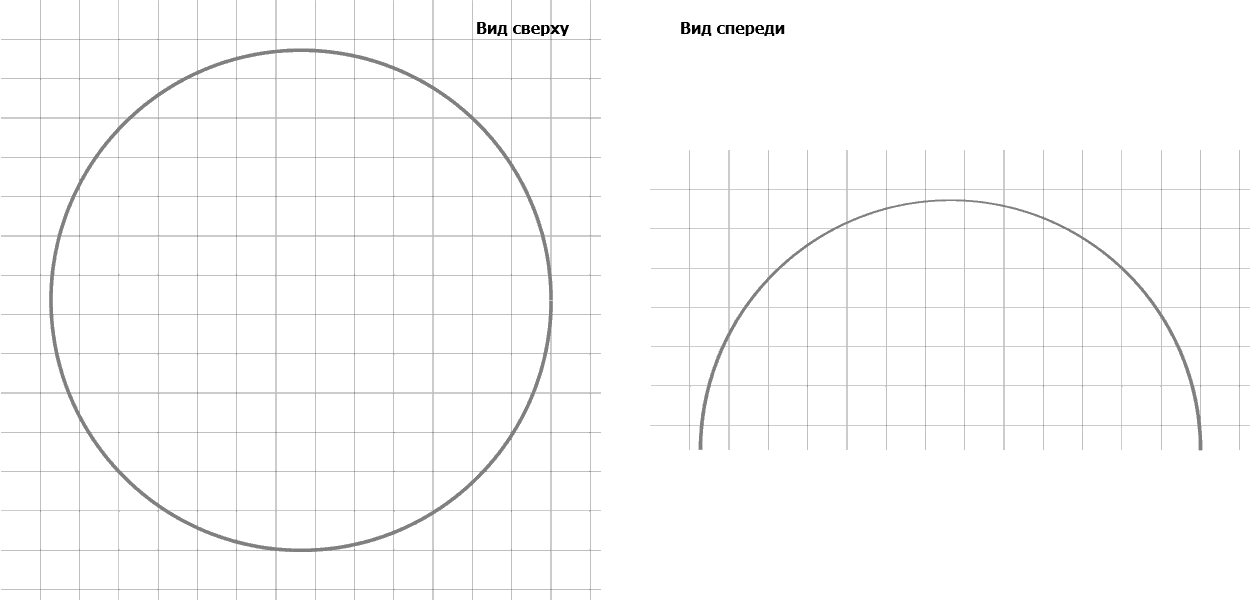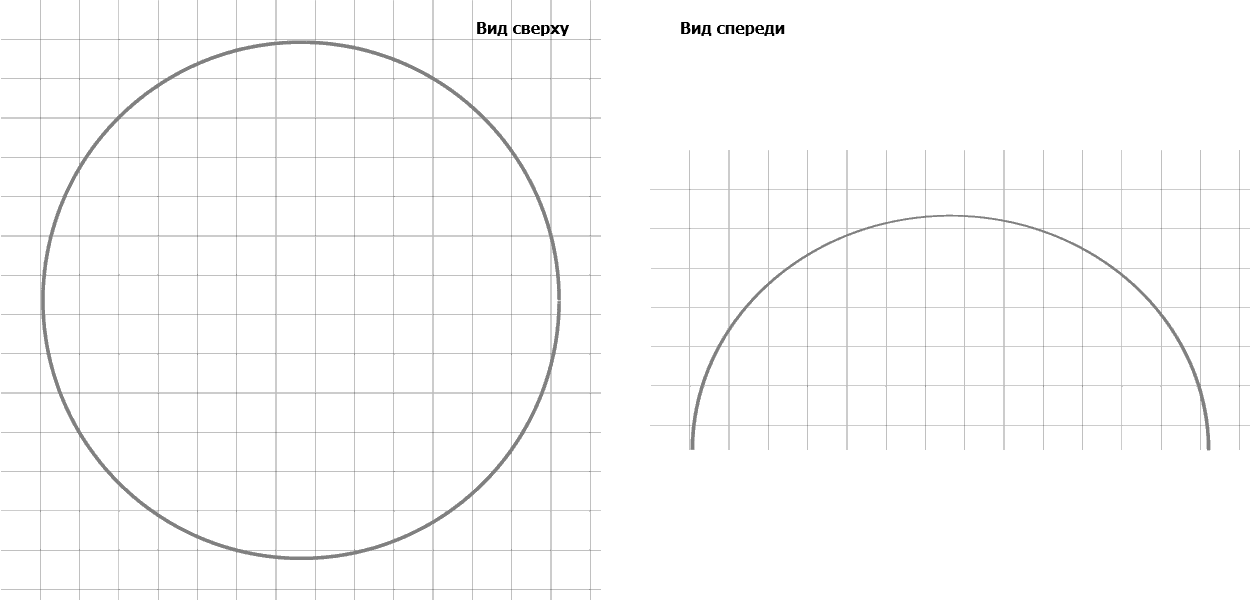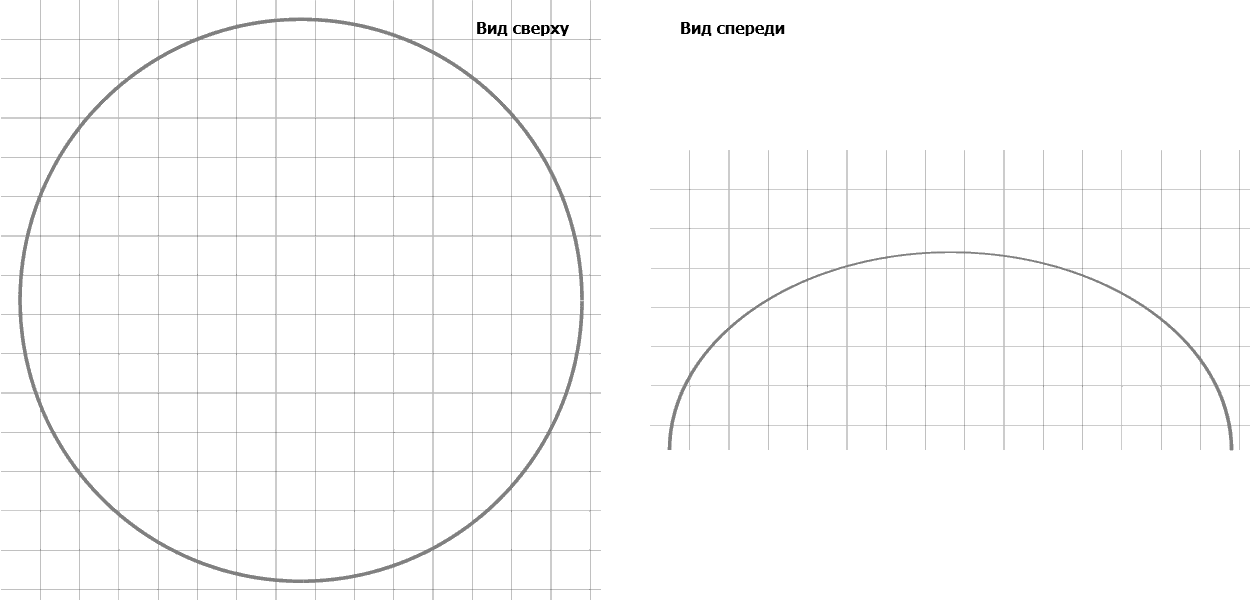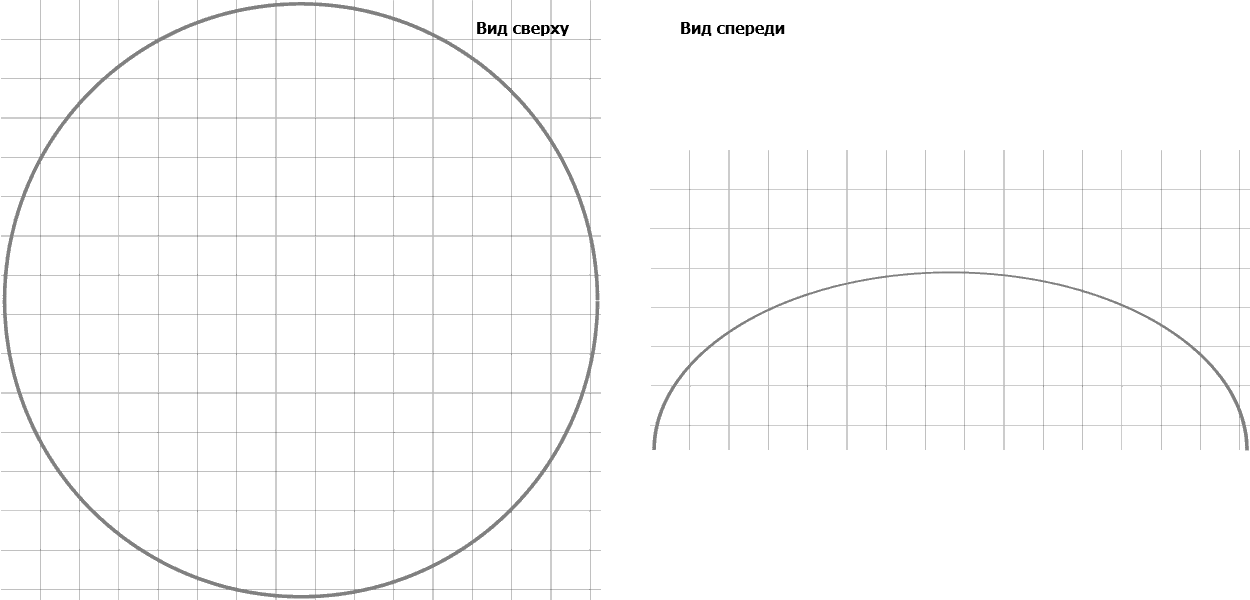
Рисунок 2 – Виды моделируемого нейтрофила сверху и спереди в процессе прикрепления
(анимация: 5 кадров, 5 циклов повторения, 118 килобайт)

Заключение

На данный момент в программе произведен расчет геометрических параметров клетки крови в различные моменты времени. Система позволяет менять входные данные и управлять вычислениями и визуализацией с помощью соответствующих панелей и настроек моделирования. Следующим и окончательным этапом работы по данной теме является построение трехмерной модели нейтрофила в процессе прикрепления.

На момент написания данного реферата магистерская работа еще не завершена. Окончательное завершение планируется на декабрь 2013 г. Полный текст работы и материалы по теме могут быть получены у автора или руководителя после указанной даты.

Список источников

1. Трехмерная графика и ее роль в освоении медико-биологических дисциплин/ Интернет-ресурс. – Режим доступа: www/ URL: http://www.pandia.ru/text/77/376/21891.php – Загл. с экрана.
2. OpenGL. Программирование компьютерной графики . Для профессионалов. – Спб.: Питер, 2002. – 1088 с. : с. 36.
3. И.Г.Герасимов, Т.М.Гальбурт. Морфометрия нейтрофилов крови человека в процессе их фагоцитоза in vitro. Вісник Донецького національного університету, Сер. А: Природничі науки, 2009, вип. 1.
4. Привалов М.В., Герасимов И.Г. Моделирование процесса прикрепления нейтрофилов крови in vitro с применением методов цифровой обработки изображений // Интеллектуальные системы принятия решений и прикладные аспекты информационных технологий: материалы научно-практической конференции ["ISDMIT’2006"], Т. 1. – Херсон: Издательство Херсонского морского института, 2006. – С. 57-59. – Бібліогр.: с. 59.
5. Герасимов И. Г., Привалов М. В., Гринченко А. А. Прогнозирование параметров процесса прикрепления клеток крови in vitro. Наукові праці Донецького нац. техніч. унів. Сер.: Обчислювальна техніка та автоматизація, г. Донецк, 2008. – С. 77–81.
6. Фомичёв К.А., Герасимов И.Г.Компьютерная система моделирования жизнедеятельности клетки крови. Матерiали II мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2011, Том 3, с. 230-234.
7. Фомичев К.А., Герасимов И.Г. Компьютерная система расчета морфометрических параметров клетки и моделирования процесса прикрепления клетки. Матерiали II мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2011, Том 2, с. 155-158.
8. Полигональные сетки/ Интернет-ресурс. – Режим доступа: www/ URL: http://compgraph.ad.cctpu.edu.ru/PolygonNet.htm – Загл. с экрана.
9. Введение в компьютерную графику/ Интернет-ресурс. – Режим доступа: www/ URL: http://ru.convdocs.org/docs/index-63233.html?page=23 – Загл. с экрана.
10. Д.В.Беклемишев. Курс аналитической геометрии и линейной алгебры: 9-е изд., перераб. М.: Физматлит, 2001. 376 с.
11. Введение в WPF/ Интернет-ресурс. – Режим доступа: www/ URL: http://metanit.com/sharp/wpf/1.php – Загл. с экрана.