Compte rendu

Contenu

1. Introduction
2. Les objectifs et les tâches du travail
3. Motivation
4. L'aperçu des études et du élaborer
   1. L'aperçu local
   2. L'aperçu global
5. Le résumé des résultats personnels
6. Conclusion
7. Bibliographie

Introduction

En peu de temps de l'existence du 3D-graphique a trouvé l'application dans de différents domaines: développement des jeux informatiques, la médecine, la conception, le design et les sphères plusieurs autres [1].

Une des directions de l'utilisation les 3D-graphiques dans la médecine est la création des 3D-modèles des organismes, des articulations, les carreaux etc. le modelage En trois dimensions permet aussi de créer les vidéoroulettes sur les sujets médicaux [1].

Souvent, l'utilisation de graphiques tridimensionnels pour démontrer les divers processus physiologiques tels que la circulation du sang dans les vaisseaux, la formation de plaques de cholestérol, la multiplication des virus, etc ainsi, il est possible de voir la dynamique de nombreux processus qui ne pouvaient auparavant regarder sur des images statiques [1].

Les objectifs et les tâches du travail

Le but du travail est l'élaboration du specialisees d'ordinateur système, qui construira l'approchée le modèle en trois dimensions des cellules sanguines dans le processus de fixation.

Pour l'exécution du but posé il est nécessaire d'accomplir une série de tâches:

1. L'étude détaillée de l'objet de l'étude et les developpement précédentes.
2. L'étude des principes et le choix des méthodes de la construction 3d des modèles.
3. L'aperçu et le choix des technologies, les milieux et le langage de programmation correspondant pour la réalisation du système informatique.
4. Élaborer l'appareil mathématique fondé sur les outils de la géométrie analytique pour le compte tous des paramètres nécessaires géométriques du neutrocyte en train de la fixation à de divers moments du temps.
5. Passer le choix des décisions existant mathématiques pour les calculs supplémentaires avec le but les définitions des paramètres numériques nécessaire à la construction 3d les modèles.
6. Élaborer de spécialiser systeme d'ordinateur, effectue le calcul des données requises, une visualisation en trois dimensions, projection États neutrophiles à des moments différents, l'affichage graphique de l'attachement de la dynamique des processus.
7. Analyser l'exactitude des résultats acquis du modelage et à leur raison de faire la conclusion sur le système élaboré.

Motivation

Un des problèmes dans la pratique de la médecine et de la cytologie a un suivi des modifications des paramètres des cellules au cours d'unele processus de leur vie. Cela permet dans une certaine mesure le degré de la conclusion de l'opération utilité.

Les données scientifiques sont souvent complexes, et les relations entre les différentes variables dans l'expérience parfoisil est difficile de visuellement. Graphics est un moyen de présenter l'information scientifique sous une formefournir une perception visuelle. Lorsque les données sont correctement substance d'essaile processus est souvent compris dans un nouveau mode [2].

Dans le travail donné il y a une observation des changements des paramètres нейтрофилов à l'expiration des laps de temps définis. l'étude de tels changements avec l'utilisation du microscope est très embarrassante et c'est pour cela que demande l'aide supplémentaire des équipements informatiques.

En train de l'observation pendant l'objet sous le microscope on peut l'examiner seulement d'une part et au présent le moment du temps. Pour voir comment les choses ont changé de forme et l'apparence d'un objet dans le temps ou à la fin de l'exécution d'un processus, il est nécessaire d'attendre une heure ou deux, voire plus, ce qui est un processus très lentobservation du sujet et de son étude. En outre sous le microscope on ne peut pas toujours considérer les domaines intéressant sous tous les aspects. C'est pourquoi, dans le travail donné on construit le modèle du neutrocyte en vue de l'économie du temps en train de l'observation pendant ces carreaux, à savoir les visualisées dans l'aspect en trois dimensions les changements géométriques du neutrocyte à de divers moments du temps.

L'aperçu des études et du développement

Comme l'étude de la dynamique du processus a été réalisée en détail l'attachement des neutrophiles dans l'Institut de recherche scientifique médicale les problèmes familiaux, l'examen de tous les trucs que le thème de l'attachement des neutrophiles, ne fera queaperçu locale et mondiale sera envoyée aux techniques de modélisation en trois dimensions.

L'aperçu local

Dans la recherche scientifique Institut a mené une étude sur les problèmes de la famille des neutrophiles. Neutrophiles étudiées dans huit échantillons 4 héparinisées (5 mk/ml) dans la phagocytose de sang capillaire bloqués à la température ambiante. On recueille le sang de volontaires sains (4 hommes, 1 femme, âgés de 19-20 ans). L'objet de la phagocytose des bactéries ont été, pris au piège d'une manière naturelle de l'environnement extérieur dans le sang après son admission. Les images numérisées des projections sur le plan des neutrophiles ont été obtenues par microscopie en immersion. Utilisé un microscope LUMAM-P3 ("LOMO") avec l'objectif X90, appareil photo numérique CCD Oscar Color Camera OS-35II ("SCAR") et un programme pour la capture, le stockage et la visualisation d'images ASUS Live Version 4.6 B2 [3].

Dans les images à l'aide d'un programme spécial projections de contour informatiques de neutrophiles ont été isolés sur un plan, comme indiqué dans la Fig. 1, mesurée périmètre (P) et de la zone (S) a été calculé et compact (C = P2/4πS) – paramètres morphométriques (M). Les paramètres des équations cinétiques, et facilité par un logiciel statistique R for Windows FAQ Version for R-2.4.1. Chaque carré contient 10 unités et les valeurs moyennes ont été calculées avec un niveau de confiance de 0,95. L'intervalle de valeurs calculées de confiance relatives de P et S ne dépassent pas ± 10% [4].

Figure 1 – Images ne sont pas en profilée et profilée neutrophiles

Dans ce document [5] ont été obtenues équations cinétiques décrivant le processus de fixation des neutrophiles sanguins humains. Les paramètres de l'équation et le calcul du temps d'achèvement de l'attachement. Les modifications des paramètres morphométriques sur le temps peut être décrit par l'équation de premier ordre:

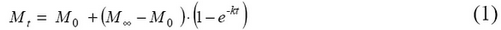
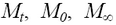où – P ou S 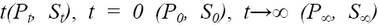, k – vitesse de premier ordre constant, .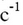

La dépendance peut aussi être décrite par une autre équation cinétique de second ordre, similaire à la première [3]:

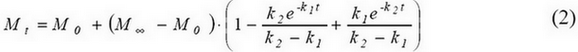
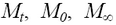où – P ou S 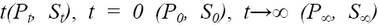, 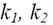– les constantes de vitesse du premier et du second ordre, .

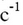En Fomichev Kirill, Gerasimov Igor discute modélisation des processus vitaux des cellules: l'attachement, la phagocytose, la transformation, la prolifération, la nécrose, l'apoptose [6]. On élabore le schéma du système spécialisé informatique pour le modelage des procès de la fixation, la phagocytose, la transformation, et la nécrose du carreau et l'image des procès donnés de l'activité vitale du carreau graduellement d'un bout à l'autre. Le modelage permet d'indiquer les paramètres initiaux géométriques du carreau, ainsi que les paramètres du milieu ambiant, qui influencent la vitesse du procès [6].

Dans le dernier article Fomichev Kirill, Gerasimov Igor aborde la modélisation des changements dans les paramètres morphométriques des cellules dans le processus de fixation. À la suite des calculs et le programme affiche des statistiques pour les modifications de paramètres lors de la fixation des cellules. Statistiques des graphiques de formulaires qui peuvent être mis à l'échelle et les paramètres du moniteur [7].

L'aperçu global

Types de modèles 3D:

Les modèles de frontière:
• représentée comme un ensemble de sommets, arêtes et polygones plats (maillage)
• représentation en utilisant les portions bicubiques paramétriques (pièces)
Hiérarchique
Hybrid

Mailles

Le maillage est un ensemble d'arêtes, les sommets et les polygones. Les sommets sont reliés par des arêtes, et les polygones sont traités en tant que séquence d'arêtes et de sommets. La grille peut être représenté de plusieurs façons différentes, chacun d'eux a ses avantageset des inconvénients. Pour évaluer la présentation optimale en utilisant les critères suivants [8]:

• La mémoire requise;
• Faciliter l'identification de l'incident bords vers le haut;
• Identifier facilement les polygones, qui appartient à l'arête donnée;
• Recherche facile procédures sommets qui forment une arête;
• Facilité définition des bords qui forment le polygone;
• Capturer facilement des images maille;
• Simple détection des erreurs dans la représentation (par exemple, pas de bords ou des sommets ou des polygones) [8].

La représentation évidente des polygones

Chaque polygone peut être représenté sous la forme d'une liste des coordonnées des sommets [8]:

Les sommets sont stockées dans l'ordre dans lequel elles se produisent sur le tour du polygone. Dans ce cas, tous les sommets successifs du polygone (ainsi que le premier et le dernier) sont reliés par des arêtes. Pour chaque méthode d'enregistrement actif polygone est efficace, cependant, pour la maille fournit la perte de mémoire due à la duplication des informations sur les coordonnées des sommets de la commune [8].

Maille de polygone est représenté en traçant chacun bords du polygone, mais elle conduit àqui part des bords sont dessinés deux fois – une fois pour chacun des polygones [8].

Polygones réglage à l'aide des pointeurs dans la liste des sommets

Lorsque vous utilisez cette représentation, chaque maille de noeud est stocké une seule fois dans la liste des sommets V =((x1, y1, z1), … , (xn, yn, zn)). Un polygone est défini par une liste de pointeurs (ou index) dans la liste de sommets. Les sommets du polygone composé de 3, 5, 7 et 10 de cette liste, est représenté en tant que P = (3, 5, 7, 10) [8].

Cette idée a un certain nombre d'avantages par rapport à la tâche explicite de polygones. Comme chaque sommet du polygone est stocké une seule fois, il est possible d'enregistrerune quantité importante de mémoire. En outre, les coordonnées des sommets peuvent être facilement changés. Mais encore juste récupérer polygones bords communs. Les côtes à l'image entièreforme polygonale encore tiré deux fois. Ces deux problèmes peuvent être résolus en décrivantnervure explicitement [8].

Définition explicite des bords

Dans cette perspective, il ya une liste de sommets V, mais est maintenant considéré comme un polygoneun ensemble de pointeurs vers des articles dans la liste des bords, dont les bords se produisent qu'une seule fois. Chaque bord de la liste de bord présente deux pics dans la liste de sommets qui définissent ce bordet un ou deux bords de polygone auquel elle appartient. Ainsi, nous pouvons polygone en tant que P = (E1, ..., E 2), et le bord – en tant que E = (V1, V2, P1, P2).Si le bord appartient à un seul polygone, puis P1 ou P2 – vide [8].

Si vous définissez explicitement les bords de maillage polygonal est représenté en traçant pas tous les polygoneset tous les bords. En conséquence, éviter dessin répété de bords communs. Certains polygones donc tout simplement dépeints comme[8].

Le filet égal

Ce modèle décrit les coordonnées des points individuels sur la surface de la manière suivante. Chaque noeud de la grille avecindices (i, j) est attribuée la valeur de la hauteur de Zij. Indices (i, j) correspondent à des valeurs spécifiques les coordonnées (x, y). La distance entre les mêmes noeuds - dx long de l'axe x, dy axe y. En fait, un tel modèle – est un tableau à deux dimensions, trame, matrice dans laquelle chaque élément stocke la valeur de la hauteur. Non chaque surface peut être représentée par ce modèle. Si chaque noeud (i, j) est enregistréune seule valeur de la hauteur, cela signifie que la surface est décrite par une fonction à valeur unique z = f (x, y). En d'autres termes, c'est une surface qui croise chaque fois vertical. Ne peut être modélisée comme faces verticales. Il convient de noter que la grille ne peut être donnée seulement en coordonnées cartésiennes. Par exemple, pour décrire la surface d'une fonction de balle-évalué, vous pouvez utiliser les coordonnées polaires [9].

Le filet non uniforme

Grille non uniforme est le modèle décrivant la surface en un ensemble de points individuels {(x0, y0, z0), (x1, y1, z1), ..., (xn-1, yn-1, zn-1)} appartiennent à la surface. Un tel modèle peutvu comme une généralisation de certains des modèles ci-dessus. Par exemple, le modèle de polygone vecteuret une grille uniforme peut être considérée comme un genre de grille non uniforme [9].

L'ensemble inégale des points de référence complique la détermination des coordonnées des autres points de la surface, qui ne coïncide pas avec le point de référence. Des méthodes spéciales d'interpolation spatiale [9].

Que la tâche consiste en calcul de la signification de la coordonnée z selon les coordonnées connues (x, y). Il est nécessaire de trouver Pour cela quelques proches points les plus, а puis calculer la signification cherchée z, à partir de la disposition mutuelle de ces points à la projection (x, y). Pour le filet égal cette tâche se décide assez simplement – la recherche est absente en réalité, paient à la fois les indices des proches points les plus d'appui [9].

La deuxième tâche consiste en image (visualisation) de la surface. On peut décider cette tâche avec plusieurs moyens. Un des plus répandu – la triangulation. Le procès de la triangulation peut être présenté comme il suit [9]:

• Nous trouvons premier trois proches points les plus l'un à l'autre – est reçu une limite plate triangulaire;
• Nous trouvons le point plus proche de cette limite, et est formé la limite contiguë, etc., il ne restera pas d'aucun point séparé.

C'est le schéma total de la triangulation. Dans la littérature on peut rencontrer la multitude d'algorithmes de la triangulation réduits vers описаному est plus haut. Un des plus répandu – la triangulation de Delone [9].

Description des faces triangulaires de surface peut déjà être considéré comme un type de vecteur modèle polygonal. Dans la littérature de langue anglaise pour son nom est abrégée TIN (réseau triangulé irrégulier). Après avoir obtenu la triangulation de surface polygonale, qui effectuent la cartographie est tout simplement [9].

Le résumé des résultats personnels

A ce stade du programme est écrit pour calculer et visualiser les changements de paramètres géométriques de globules rouges dans le processus de fixation sur le substrat. A développé un des outils mathématiques spécifiques pour calculer la hauteur des cellules au moment souhaité.

Cellule simulé apparaît comme une bille, qui, en contact avec la fixation et le substrat se déforme. La déformation est la suivante: à la fixation des cellules initiale prend la forme d'un hémisphère, en des points de temps ultérieurs jusqu'à ce que l'extrémité de la cellule de fixation aplatit et est compressible poluellipsoid, dont la base est un cercle. Ainsi, la cellule est une vue de face d'une demi-ellipse, et une vue en plan - cercles. Bases ellipse et le changement de rayon de cercle avec le temps. Contrairement forme naprotjazhenii processus de fixation du volume cellulaire total ne change pas. La zone de formule de cercle permet de calculer le rayon des cellules des paramètres morphométriques – secteur:

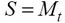, où 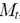calculé à partir des équations (1) ou (2). Ainsi, le rayon de la cellule à l'instant t:

Si le calcul est effectué sur le paramètre morphométrique – le pourtour, afin de calculer le rayon de la cellule besoin d'une formule de la circonférence:

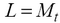, где 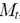calculé à partir des équations (1) ou (2). Ainsi, le rayon de la cellule à l'instant t:

La moitié du volume de l'ellipsoïde:

dans laquelle a, b, c l'axe de l'ellipsoïde: c – hauteur, a b, – l'axe majeur et mineur de l'ellipse, qui se trouve dans le sol. A l'instant initial t0 = 0 attacher cellule comme mentionné ci-dessus, est une demi-sphère de rayon R0. Dans la demi-section de la balle est une demi-ellipse avec demi a0, c0, dans laquelle c0 = a0 = R0, et le cercle de base de rayon R0 = a0 = b0. Ensuite, en fonction de la formule (7), la quantité de cellules à l'instant initial t0 est fixé:

A un instant t1 suivante commence s'allonger cellule sujette mettant en contact le substrat, ce qui modifie la hauteur et le rayon de qui sont égal à R1, et C1 respectivement. Puis le volume de la cellule à l'instant t1:

Comme le montant total de processus d'attachement naprotjazhenii inchangé, le assimilant les bons côtés des équations (8) et (9) peut être exprimée c1 de hauteur au temps t1:

dans laquelle R0 et R1 sont calculés selon les formules (4) ou (6). Hauteur obtenu par la formule (10) est une valeur initiale pour le calcul des cellules hauteurs dans les cas suivants: où i = 1, ..., n, n – nombre d'échantillons de temps.

Les valeurs estimées de rayon et la hauteur sont calculés points (xi, yi) pour la construction de l'avant et des vues de dessus:

où a, b – le rayon et la hauteur de la cellule, t – équations paramétriques,

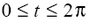
Les calculs de programme sont exécutées rayon et la hauteur de globules rouges en fonction de ses paramètres morphométriques. Le calcul des points pour la construction des types de cellules de l'avant et le haut.

Afin de développer une des entrées du système informatique sont les initiales (avant la fixation) et finales (après fixation) les paramètres morphométriques des globules rouges, ainsi que la constante pour les équations du premier et du second ordre taux [7].

Le programme développé – Windows Presentation Foundation (WPF) application, qui est utilisé pour écrire environnement de développement MS Visual Studio et la langue C#.

Été choisi plate-forme WPF, car il présente les avantages suivants:

1. Indépendant de la résolution de l'écran – comme dans tous les éléments WPF sont mesurés en unités indépendantes des périphériques, les applications WPF sont facilement extensibles à différents écrans avec des résolutions différentes.
2. Nouvelles fonctionnalités, ce qui était difficile à réaliser dans WinForms, par exemple, la création de modèles en trois dimensions, la liaison de données, etc.
3. La programmation déclarative – quelques similitudes avec balisage langues html/xml, présentant une alternative à la création des horaires et des contrôles programme.
4. Une bonne interaction avec WinForms, de sorte que, par exemple, les applications WPF peut utiliser les contrôles traditionnels de WinForms [11].

Pour démontrer les résultats du programme peuvent donner quelques données chiffrées obtenues pendant son fonctionnement, par exemple, au temps t = 0, c, t = 100 C, T = 300 C, T = 550 C, T = 1,500 c et types de cellules sur la partie supérieure et avant sont présentés dans la figure. 2. Les valeurs du rayon et de la hauteur et de ces horaires:

а=6.3662 мкм, с=6.3662 мкм;
а=6.57 мкм, с=5.9763 мкм;
а=6.8863 мкм, с=5.4389 мкм;
а=7.1534 мкм, с=5.0413 мкм;
а=7.5472 мкм, с=4.5295 мкм.

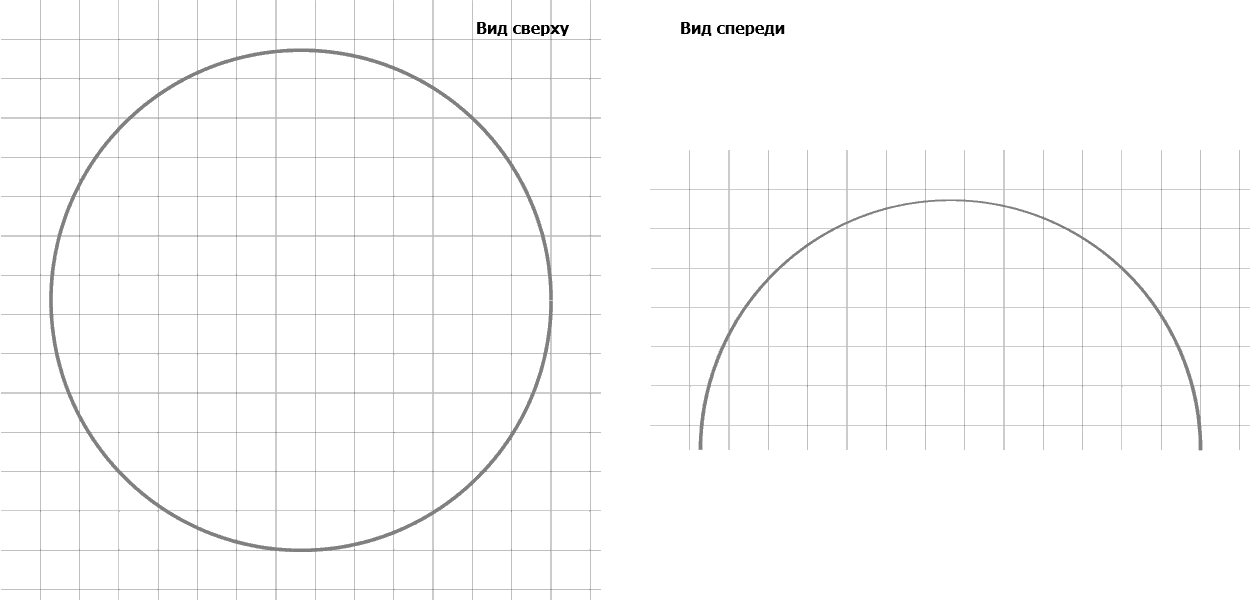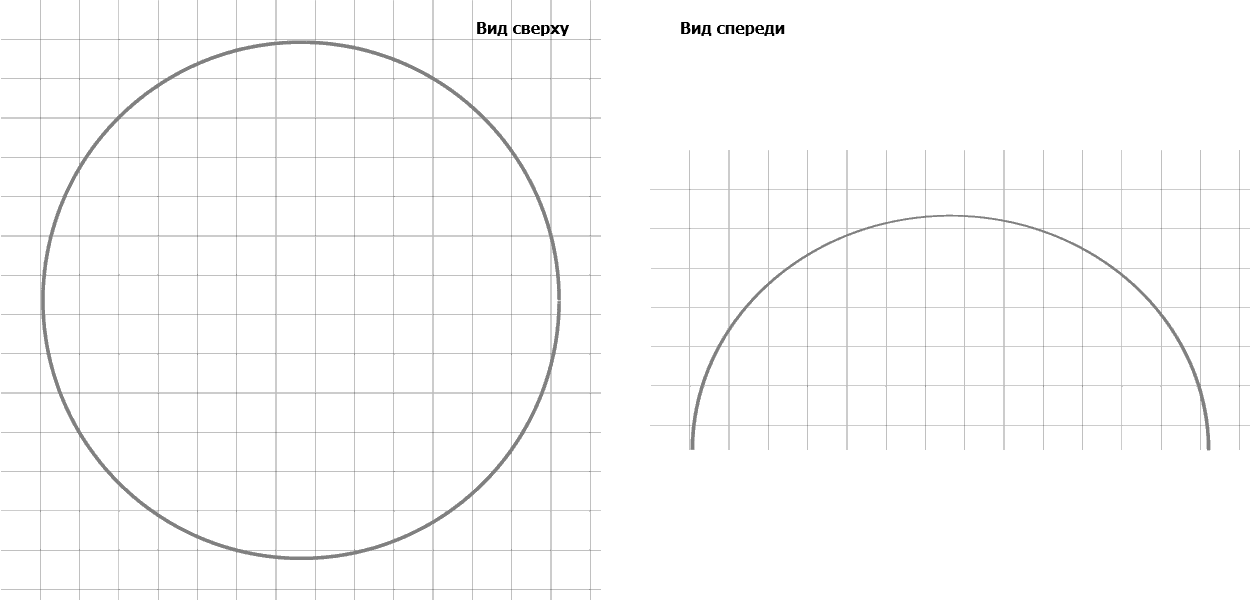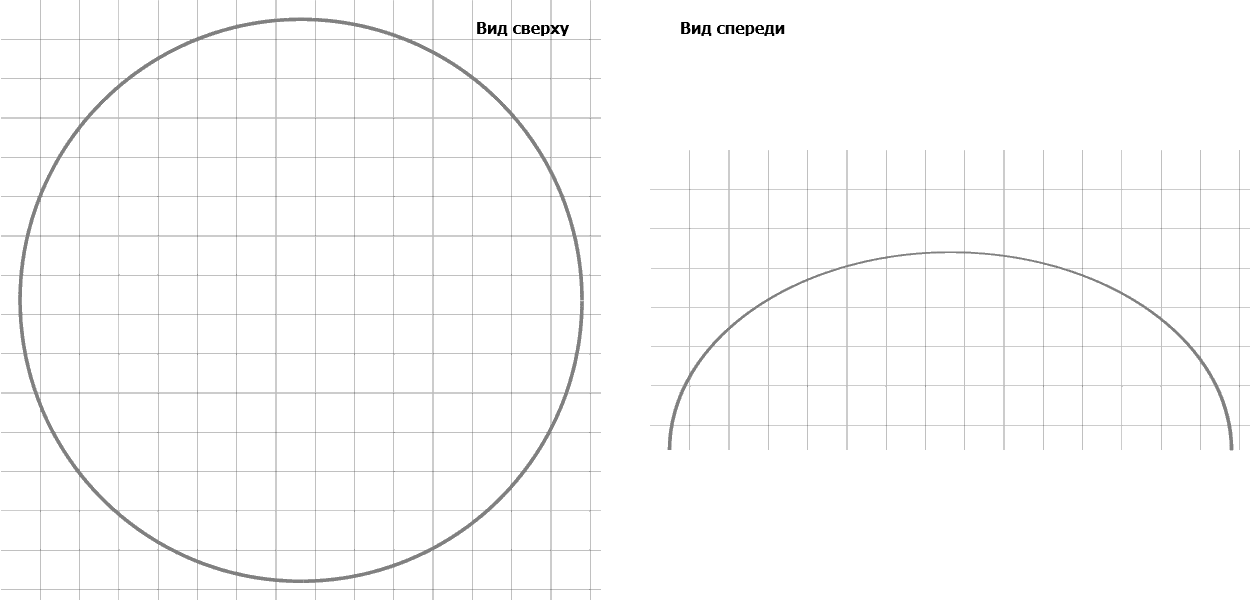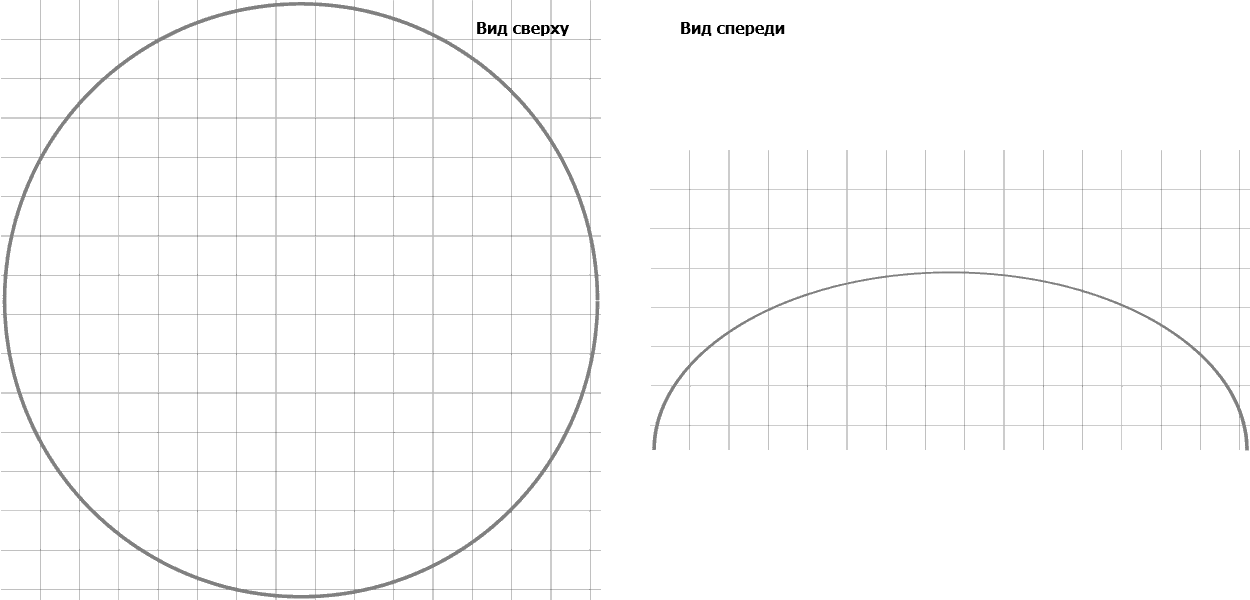
Figure 2 – Types de haut de neutrophiles simulé et avant dans le processus de l'attachement
(Animation: 5 tirs, 5 cycles de répétition, 118 KB)

Conclusion

A ce stade, dans le programme calculé les paramètres géométriques de globules rouges à différents points dans le temps. Le système vous permet de modifier les données d'entrée et de gérer l'informatique et la visualisation en utilisant les paramètres et la simulation de panneaux appropriés. La prochaine et dernière étape des travaux sur ce sujet est de construire un modèle tridimensionnel de l'élastase dans la pièce jointe.

Au moment de la rédaction de l'œuvre de ce maître de l'essai n'est pas encore terminée. La réalisation définitive est prévue pour Décembre 2013 Text complète des travaux et des matériaux sur le sujet peuvent être obtenus auprès de l'auteur ou de la tête après cette date.

Bibliographie

1. Трехмерная графика и ее роль в освоении медико-биологических дисциплин/ Интернет-ресурс. – Режим доступа: www/ URL: http://www.pandia.ru/text/77/376/21891.php – Загл. с экрана.
2. OpenGL. Программирование компьютерной графики . Для профессионалов. – Спб.: Питер, 2002. – 1088 с. : с. 36.
3. И.Г.Герасимов, Т.М.Гальбурт. Морфометрия нейтрофилов крови человека в процессе их фагоцитоза in vitro. Вісник Донецького національного університету, Сер. А: Природничі науки, 2009, вип. 1.
4. Привалов М.В., Герасимов И.Г. Моделирование процесса прикрепления нейтрофилов крови in vitro с применением методов цифровой обработки изображений // Интеллектуальные системы принятия решений и прикладные аспекты информационных технологий: материалы научно-практической конференции ["ISDMIT’2006"], Т. 1. – Херсон: Издательство Херсонского морского института, 2006. – С. 57-59. – Бібліогр.: с. 59.
5. Герасимов И. Г., Привалов М. В., Гринченко А. А. Прогнозирование параметров процесса прикрепления клеток крови in vitro. Наукові праці Донецького нац. техніч. унів. Сер.: Обчислювальна техніка та автоматизація, г. Донецк, 2008. – С. 77–81.
6. Фомичёв К.А., Герасимов И.Г.Компьютерная система моделирования жизнедеятельности клетки крови. Матерiали II мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2011, Том 3, с. 230-234.
7. Фомичев К.А., Герасимов И.Г. Компьютерная система расчета морфометрических параметров клетки и моделирования процесса прикрепления клетки. Матерiали II мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. – Донецьк, ДонНТУ – 2011, Том 2, с. 155-158.
8. Полигональные сетки/ Интернет-ресурс. – Режим доступа: www/ URL: http://compgraph.ad.cctpu.edu.ru/PolygonNet.htm – Загл. с экрана.
9. Введение в компьютерную графику/ Интернет-ресурс. – Режим доступа: www/ URL: http://ru.convdocs.org/docs/index-63233.html?page=23 – Загл. с экрана.
10. Д.В.Беклемишев. Курс аналитической геометрии и линейной алгебры: 9-е изд., перераб. М.: Физматлит, 2001. 376 с.
11. Введение в WPF/ Интернет-ресурс. – Режим доступа: www/ URL: http://metanit.com/sharp/wpf/1.php – Загл. с экрана.