Реферат по теме выпускной работы

Содержание

Введение

Сложные сетевые динамические объекты с распределенными параметрами (СДОРП) различных предметных областей требуют при их исследовании высокопроизводительных средств и методов решения многомерных систем уравнений, а также компьютерной поддержки всех этапов разработки и применения средств моделирования [1, 2]. Модель СДОРП – это формальное представление топологии и система дифференциальных уравнений в частных производных, описывающих динамические процессы в ветвях и узлах объекта. Simulation-моделью (SM) принято называть модель, преобразованную к виду, удобному для применения численных методов. Дискретную Simulation-модель (DSM) получают посредством аппроксимации SM-уравнений, граничных и начальных условий расчетными формулами выбранного численного метода. Аппаратно-программная реализация DSM представляет собой решатель системы уравнений модели. СДОРП-симулятор реализует все этапы работ по моделированию – от представления топологии объекта до проведения модельных экспериментов. Перспективным направлением является разработка СДОРП-симуляторов в составе распределенных параллельных моделирующих сред (РПМС) общего и проблемно-ориентированного назначения [2]. При этом наряду с известными численными методами, применяемыми в последовательных языках моделирования и реализуемыми в РПМС, требуется построение параллельных решателей на основе новых блочных численных методов [3].

1. Актуальность темы

Сегодняшние дни характеризуются стремительными темпами роста различных технологий. То, что несколько лет назад было актуальным, сегодня уже может быть просто никому не нужно. Поэтому можно смело утверждать, что именно сейчас на первый план выходит моделирование как инструмент, который способен еще на этапе проектирования определить оптимальные параметры будущего устройства, выявить скрытые недостатки, оценить поведение при тех или иных условиях. Хорошая модельная поддержка способна увеличить тот срок пребывания устройства на рынке, когда оно еще актуально. Чем более массовым является производство, тем более важную роль играет в нем моделирования. Например, при проектировании автоматизированных технических объектов, технологических установок и линий, которые определяются как сложные динамические системы (СДС), на первый план выходит именно оно.

Последнее время формируются новые направления разработок и исследований – параллельное моделирование (Parallel Simulation Technology, Parallele Simulationstechnik), территориально распределенное моделирование на базе GRID-технологий. Центральной проблемой параллельного моделирования сложных динамических систем является построение распределенных параллельных моделирующих сред (РПМС) универсального и специализированного назначения.

2. Цель работы

Целью работы является разработка MIMD-симулятора управляемого сетевого динамического объекта с распределёнными параметрами и его интегрирование в систему полунатурного моделирования.

3. Основные задачи работы

1. Создание последовательного симулятора сетевого динамического объекта с распределёнными параметрами.

2. Разработка параллельного MIMD-симулятора управляемого сетевого динамического объекта с распределёнными параметрами.

3. Оптимизация работы MIMD-симулятора для интеграции в систему полунатурного моделирования.

4. Состояние разработок распределенных параллельных моделирующих сред

Концепция распределенной параллельной моделирующей среды (РПМС) для сложных динамических систем с сосредоточенными и распределенными параметрами была предложена в 1992 г. в рамках научного сотрудничества факультета ВТИ ДонНТУ и института параллельных и распределенных систем (IPVS) Штуттгартского университета (Германия), опубликовано в Asim-докладе [4] и развито в работах [7, 8, 9, 10]. РПМС называется такая системная организация совместного функционирования параллельных аппаратных ресурсов, системного и моделирующего программного обеспечения, которая поддерживает все этапы разработки, реализации и применение параллельных моделей СДС [5].

Главным положением РПМС-концепции является необходимость полнофункциональной разработки параллельных методов и алгоритмов функционирования моделирующего программного обеспечения (Modeling and Simulation Software) для ДСРП. Анализ показывает, что параллельные системы SIMD- и MIMD-структур 90-х годов имели фирменные языки параллельного программирования, которые базируются на языках Fortran, C, C++, Modula-2 и др. Развитие параллельных вычислительных систем Mimd-архитектуры, объектно-ориентированных подходов стимулировал стандартизацию средств параллельного и распределенного программирования. Так, ANSI и ISO определили С++-стандарты с библиотеками MPI, PVM и Pthreads. Концепция предусматривает обеспечить пользователей и разработчиков параллельных моделей языковыми и системно-организационными средствами, которые по уровню сервиса будут превосходить системы и языки моделирования пятого поколения [6]. В этом направлении проведены разработки относительно обобщения топологий СДС, а комплексы «топологические анализаторы – генераторы уравнений – решатели» транслируют описания СДС уровня предметной области в параллельные программы [5].

5. Формальное описание (модель) и постановка задачи параллельного моделирования СДОРП

Топология аэродинамического сетевого динамического объекта характеризуется графом G (m, n), который кодируется таблицей (1) и имеет m строк и s +3 столпцов. Здесь Qj – поток воздуха в ветви j; ПУ и КУ соответствующие начальному и конечному узлам j-ветви; PAR(PJ1, PJ2, …, PJs) – множество s параметров Pj каждой ветви.

Таблица 1. Исходное кодирование графа G (m, n)

ПУ КУ Qj PAR(PJ1, PJ2, …, PJs)

Для j-й ветви, которая не имеет утечек воздуха, динамика расхода и давления описываются системой уравнений (1).

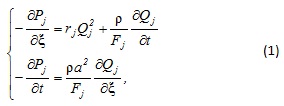
В которой Pj,Qj – давление и расход воздуха вдоль координаты ξ, которая отсчитывается от начального ПУ до конечного КУ узлов; rj – удельное аэродинамическое сопротивление; Fj – площадь поперечного сечения ветви; ρ – плотность воздуха; a – скорость распространения звука в воздухе.

Граничные условия для системы уравнений (1) – это функции давления в начальном PПУ и конечном PКУ узлах ветви j. По типу граничных условий ветви сети делятся на три вида:

- ветви, инцидентные внутренним узлам сети, в которых давление рассчитывается в процессе решения сетевой системы уравнений в соответствии с узловыми динамическими условиями

Где Pwj – давление в узле wj; Qwj – суммарный поток воздуха в узле wj; Fwj – площадь поперечного сечения j-й ветви в узле;

- ветви, инцидентные узлу подключения вентилятора, и в этом узле давление задается как характеристика вентилятора

- ветви, инцидентные узлу выхода в атмосферу, здесь принимается постоянное давление атмосферы

6. Дискретизирование по пространственной координате Simulation-модели j-й ветви и всего СДОРП

В результате аппроксимации системы уравнений (1) методом прямого с шагом Δξ по пространственной координате получим следующие уравнения для k-ого элемента j-й ветви:

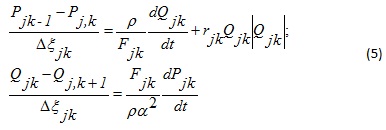
Для аэродинамического объекта с распределенными параметрами каждая ветвь представляется в виде двух векторов Qj, Pj (j = 1 ... m):

- поток воздуха в j-ой ветви

- давление в j-й ветви

При этом количество элементов в векторах

исчисляется по длинам ветвей Lj и единому для СДОРП шагу Δξ.

Дискретизированная по пространственной координате модель j-ветви содержит Mj систем уравнений (6) при k = 1,2, ..., Mj. Для вычисления компонент векторов (6), (7) приведем систему (5) к форме пространственно-дискретизированной Simulation-модели (ПДSM).

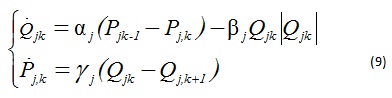
Коэффициенты αj, βj, γj, зависят от параметров j-ветви.

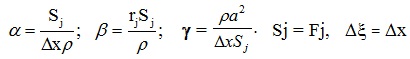
7. Формирование уравнений для заданного сетевого объекта с распределенными параметрами

Сетевой динамический объект задан граф схемой, приведенной на рисунке 1. Уравнения для этого объекта составлены по системе (9).

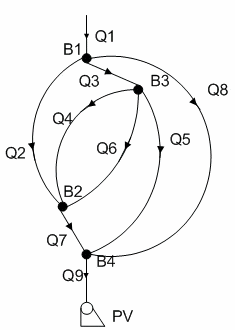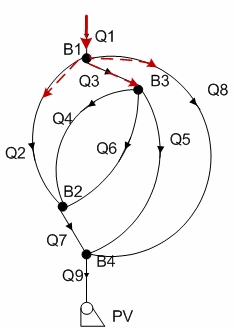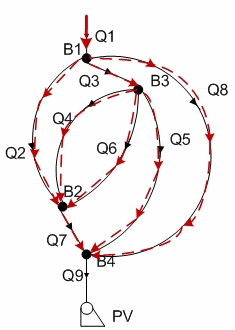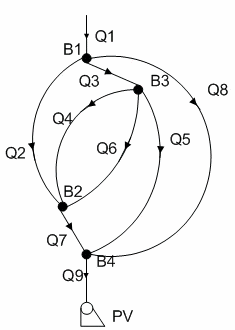
Граф схема сетевого динамического объекта (анимация: 8 кадров, 5 цикла повторения, 20,5 Кб)

Рисунок 1 – Граф схема сетевого динамического объекта
(анимация: 8 кадров, 5 цикла повторения, 20,5 Кб)

Система уравнений для объекта

Q1:

Q9:

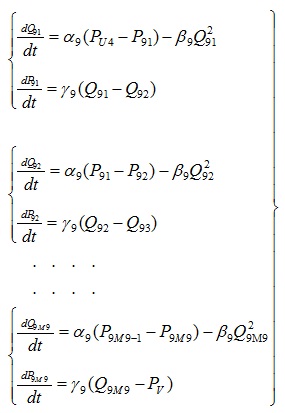
Выводы

Для параллельного моделирования сложных сетевых динамических объектов с распределенными параметрами необходима алгоритмическая и программная поддержка построения решателей уравнений. В работе предложена и проиллюстрирована методика преобразования исходной модели СДОРП в дискретную. Этапы преобразований служат базой для реализации MIMD-симулятора в составе распределенной параллельной моделирующей среды.

При написании данного реферата магистерская работа ещё не завершена. Окончательное завершение: декабрь 2013. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Svjatnyj V., Moldovanova O., Smagin A., Resch M., Keller R., Rabenseifner R.: Virtuelle Simulationsmodelle und ein Devirtualisierungsvorgang fur die Entwicklung der parallelen Simulatoren von komplexen dynamischen Systemen. In: DonNTU, FRTI-Werke, Reihe "Probleme der Modellierung und rechnergestutzten Projektierung von dynamischen Systemen", Band 5(116). – Donezk, 2006. – S. 36–43.
  2. Feldmann L.P., Resch M., Svjatnyj V.A., Zeitz M.: Forschungsgebiet: parallele Simulationstechnik. In: DonNTU, FRTI-Werke, Reihe "Probleme der Modellierung und rechnergestutzten Projektierung von dynamischen Systemen", Band 9(150). – Donezk, 2008. – S. 9-36.
  3. Фельдман Л.П., Назарова И.А. Параллельные алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений. //Математическое моделирование, том 18, №6, 2006.- С.17-31.
  4. Святний В.А., Молдованова О.В.,Чут А.М.: Стан та перспективи розробок паралельних моделюючих середовищ для складних динамічних систем з розподіленими та зосередженими параметрами.
  5. Schmidt B. Simulationssyteme der 5. Generation - SiP, Heft 1, 1994, S. 5-6.
  6. Бройнль Т. Паралельне програмування: Початковий курс: Навч. посiбник / Переклад з нiм. В. А. Святного. - К.: Вища шк., 1997. - 358 с.
  7. Feldmann L., Svjatnyj V., Lapko V., Gilles E.-D., Reuter A., Rothermel K., Zeitz M. Parallele Simulationstechnik. // Научные труды ДонГТУ, серия «Проблемы моделирования и автоматизации проектирования динамических систем», вып. 10. – Донецк, 1999. – С. 9–19.
  8. Svjatnyj V., Gilles E.-D., Zeitz M., Reuter A., Rothermel K. Simulationssoftware fur eine parallele Simulationsumgebung fur dynamische Systeme. 14. Symposium ASIM 2000. – Tagungsband, SCS, 2000. – S. 235–240.
  9. Moldovanova O.V., Svjatnyj V.A., Feldmann L., Resch M., Kuster U.: Problemorientierte parallele Simulationsumgebung. // Научные труды ДонНТУ, серия «Информатика, кибернетика и вычислительная техника», вып. 93. – Донецк, 2005. – С. 145–150.
  10. Святний В.А. Паралельне моделювання складних динамічних систем // Моделирование – 2006: Международная конференция. Киев, 2006 г. – Киев, 2006. – С. 83–90.