Abstract

Content

Introduction

Complex networking dynamic objects with distributed parameters (NDODP) of different domains require in their research of high-performance tools and methods for the solution of multi-dimensional systems of equations, as well as computer support all phases of the development and application of modeling tools [1, 2]. NDODP model is the formal presentation of the topology and the system of differential equations describing the dynamic processes in the branches and nodes of the object. Simulation-model (SM) is a model converted to a form suitable for the application of numerical methods. Simulation-discrete model (DSM) is obtained by fitting the SM-equations, boundary and initial conditions calculation formulas chosen numerical method. The hardware and software implementation of DSM is a solver of the model equations. SDORP simulator implements all the stages of modeling work – from the view of the topology of the object to the model experiments. A promising direction is the development of NDODP simulators in the distributed parallel modeling environments (DPME) general and task-oriented destination [2]. Along with the known numerical methods used in sequential modeling languages and implemented in the DPME, requires the construction of parallel solvers based on the new block numerical methods [3].

1. Relevance of the topic

Current days are characterized by a rapid rate of growth of various technologies. The fact that a few years ago, it was relevant, today it may just be unnecessary. Therefore, we can safely say that it is now at the forefront modeling as a tool that is capable of at the design stage to determine the optimal parameters of the future devices, detect latent defects, to evaluate the behavior under certain conditions. A good model is able to enhance that support tenure devices on the market, when it is still relevant. The more massive is the production, the more important the role it plays in the simulation. For example, in the design of automated technical facilities, processing plants and transmission lines, which are defined as a complex dynamic system (CDS), comes to the fore exactly it.

Recently are formed new developments and research directions – parallel simulation (Parallel Simulation Technology, Parallele Simulationstechnik), geographically distributed simulations based on GRID-technologies. The central problem of the parallel simulation of complex dynamic systems is to build a distributed parallel simulation environments (DPME) of the universal and specialized purpose.

2. Goal of the work

The goal is to develop a MIMD-simulator of the manageable networking dynamic object with distributed parameters and integrate it into the semi-natural modeling system.

3. Main tasks of the work

1. Creation of a sequential simulator of networking dynamic object with distributed parameters .

2. Development of parallel MIMD-simulator of the manageable networking dynamic object with distributed parameters.

3. Optimization of the MIMD-simulator for integration into the semi-natural modeling system.

4. The state of development of distributed parallel modeling environments

The concept of distributed parallel modeling environment (DPME) for complex dynamic systems with lumped and distributed parameters was proposed in 1992 in the framework of scientific cooperation faculty CST Donetsk National Technical University and the Institute of Parallel and Distributed Systems (IPDS) University of Stuttgart (Germany), published in Asim-report [4]and developed in the works [7, 8, 9, 10]. DPME called such systematic organization of joint functioning parallel hardware resources, systems and modeling software that supports all phases of design, implementation and application of parallel models of CDS [5].

The main position of RPMS-concept is the need to develop a fully functional parallel methods and algorithms for simulating the operation of software (Modeling and Simulation Software) for DSDP. The analysis shows that the parallel system of SIMD-and MIMD-structures of the 90s had branded a parallel programming language, which are based on languages Fortran, C, C++, Modula-2, etc. The development of parallel computing systems Mimd-architecture, object-oriented approaches stimulated a standardization of parallel and distributed programming. For example, ANSI and ISO standards define the C++ standard libraries with MPI, PVM and Pthreads. The concept is to bring users and developers of parallel models of language and system organizational means that the level of service will exceed the system and the fifth generation of modeling languages [6]. In this direction carried out the development in relation to generalization CDS topologies and complex "topological analyzers – generators of equations – solvers" broadcast description of CDS-level domain in parallel programs [5].

5. Formal description (model) and problem definition of NDODP parallel modeling

The topology of aerodynamic network dynamic object is characterized by graph G (m, n), which is encoded by the table (1) and has m rows and s +3 columns. Here Qj – air flow in the branch j; SN and EN appropriate start and end nodes of j-branch; PAR(PJ1, PJ2, …, PJs) – set of parameters Pj of each branch.

Table 1. The initial encoding of the graph G (m, n)

SN EN Qj PAR(PJ1, PJ2, …, PJs)

For the j-th branch, which has no air leaks, pressure and flow dynamics are described by the equations (1).

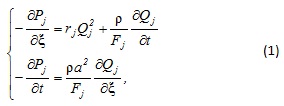
Where Pj,Qj – pressure and flow of air along the coordinate ξ, which is measured from the start SN to the end EN nodes; rj – specific aerodynamic resistance; Fj – cross sectional area of the branch; ρ – air density; a – the speed of sound in air.

The boundary conditions for the system of equations (1) are functions of the pressure in the start PSN and end PEN nodes of branch j. According to the type of boundary conditions, branchts of network are divided into three types:

- branches, which are incident to the internal nodes of the network, in which the pressure is calculated in the process of solving the networking system of equations in accordance with the terms of the nodal dynamic

Where Pwj – pressure in node wj; Qwj – total air flow in node wj; Fwj – cross sectional area of j-th branch in the node;

- branches, which are incident to the node connecting the fan and in this node the pressure is defined as a characteristic of blower

- branches, which are incident to the node of output into atmosphere, there is adopted the constant pressure of the atmosphere

6. Discretising on the spatial coordinate of Simulation-model of a branchj and all NDODP

As a result of approximation of equations system (1) by direct method with a step Δξ along the spatial coordinate we obtain the following equations for the k-th element of the j-th branch:

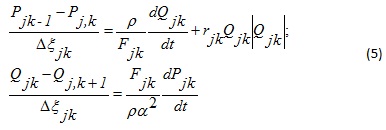
For aт aerodynamic object with distributed parameters of each branch is represented by two vectors Qj, Pj (j = 1 ... m):

- air flow in the j-th branch

- pressure in j-th branch

The number of elements in vectors

calculated from the lengths of the branches Lj and the single step for NDODP Δξ.

Discretize along the spatial coordinate model j-branch contains Mj systems of equations (6) for k = 1,2, ..., Mj. To calculate the components of the vectors (6), (7) present system (5) to form a spatially discretized Simulation-model (SDSM).

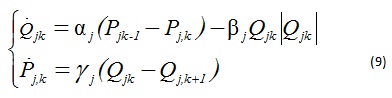
The coefficients αj, βj, γj, depend on the parameters of j-branch.

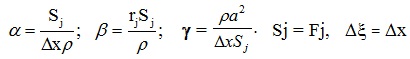
7. Formation of equations for a given networking object with distributed parameters

The networking dynamic object given as a graph diagram shown in Figure 1. The equations for this object are written according to the system (9).

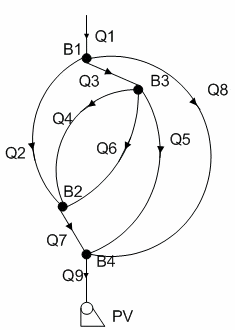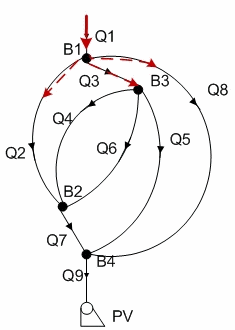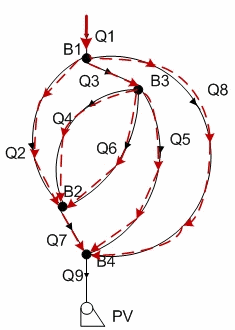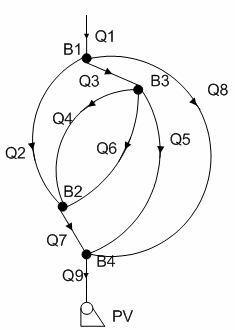
Graf diagram of a networking dynamic object (animation: 8 frames, 5 cycles of reiteration, 20,5 Кb)

Figure 1 – Graf diagram of a networking dynamic object
(animation: 8 frames, 5 cycles of reiteration, 20,5 Кb)

The system of equations for the object

Q1:

Q9:

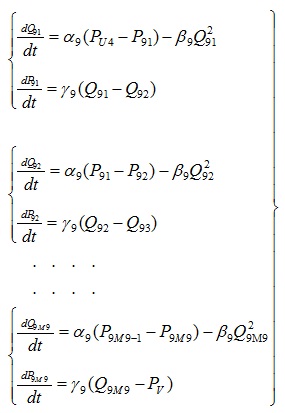
Conclusion

For parallel modeling of complex networking dynamic objects with distributed parameters is necessary algorithmic and software support for the construction of equations solvers. In work the methodology of transformation of the NDODP initial model into the discrete model is offered and illustrated. Stages of transformations are the foundation of a MIMD-simulation in a distributed parallel simulation environment.

Master's work is not yet complete. Final completion: December 2013. Full text of the work and materials on the topic can be obtained from the author or his scientific adviser after that date.

References

  1. Svjatnyj V., Moldovanova O., Smagin A., Resch M., Keller R., Rabenseifner R.: Virtuelle Simulationsmodelle und ein Devirtualisierungsvorgang fur die Entwicklung der parallelen Simulatoren von komplexen dynamischen Systemen. In: DonNTU, FRTI-Werke, Reihe "Probleme der Modellierung und rechnergestutzten Projektierung von dynamischen Systemen", Band 5(116). – Donezk, 2006. – S. 36–43.
  2. Feldmann L.P., Resch M., Svjatnyj V.A., Zeitz M.: Forschungsgebiet: parallele Simulationstechnik. In: DonNTU, FRTI-Werke, Reihe "Probleme der Modellierung und rechnergestutzten Projektierung von dynamischen Systemen", Band 9(150). – Donezk, 2008. – S. 9-36.
  3. Фельдман Л.П., Назарова И.А. Параллельные алгоритмы численного решения задачи Коши для систем обыкновенных дифференциальных уравнений. //Математическое моделирование, том 18, №6, 2006.- С.17-31.
  4. Святний В.А., Молдованова О.В.,Чут А.М.: Стан та перспективи розробок паралельних моделюючих середовищ для складних динамічних систем з розподіленими та зосередженими параметрами.
  5. Schmidt B. Simulationssyteme der 5. Generation - SiP, Heft 1, 1994, S. 5-6.
  6. Бройнль Т. Паралельне програмування: Початковий курс: Навч. посiбник / Переклад з нiм. В. А. Святного. - К.: Вища шк., 1997. - 358 с.
  7. Feldmann L., Svjatnyj V., Lapko V., Gilles E.-D., Reuter A., Rothermel K., Zeitz M. Parallele Simulationstechnik. // Научные труды ДонГТУ, серия «Проблемы моделирования и автоматизации проектирования динамических систем», вып. 10. – Донецк, 1999. – С. 9–19.
  8. Svjatnyj V., Gilles E.-D., Zeitz M., Reuter A., Rothermel K. Simulationssoftware fur eine parallele Simulationsumgebung fur dynamische Systeme. 14. Symposium ASIM 2000. – Tagungsband, SCS, 2000. – S. 235–240.
  9. Moldovanova O.V., Svjatnyj V.A., Feldmann L., Resch M., Kuster U.: Problemorientierte parallele Simulationsumgebung. // Научные труды ДонНТУ, серия «Информатика, кибернетика и вычислительная техника», вып. 93. – Донецк, 2005. – С. 145–150.
  10. Святний В.А. Паралельне моделювання складних динамічних систем // Моделирование – 2006: Международная конференция. Киев, 2006 г. – Киев, 2006. – С. 83–90.