Мішустін Сергій Михайлович

Вступ

В останні роки інтенсивно розробляється науковий напрямок з назвою «Природничі обчислення» (Natural Computing), що об'єднує математичні методи, в яких закладені принципи природних механізмів прийняття рішень. Ці механізми забезпечують ефективну адаптацію флори і фауни до навколишнього середовища протягом декількох мільйонів років.

З наших сучасників областю природничих обчислень займаються С. Янг, Г. Бені, Дж. Ванг, М. Дориго, а також вітчизняні дослідники С.А. Субботін, А.А. Олійник, В.К Яценко та багато інших.

Прикладами алгоритмів, заснованих на природних обчисленнях, є: алгоритм мурашиних колоній, алгоритм оптимізації на основі переміщення бактерій, алгоритм рою частинок, а також генетичний алгоритм.

Однією з областей застосування таких алгоритмів є область розпізнавання образів, яка в наш час широко застосовується для розпізнавання жестів, в тому числі і на пристроях з multitouch інтерфейсами.

В основі створення сучасних multitouch інтерфейсів лежить алфавіт жестів на площині. Математична модель цих жестів являє собою двовимірні форми об'єктів. Наприклад, дуга може бути жестом обертання, пряма – масштабування або переміщення.

Для найкращих результатів розпізнавання використовуються багатоагентні системи. Багатоагентною системою в даному випадку може виступати як алгоритм, що використовує безліч агентів, наприклад: алгоритм мурашиної колонії, бджолиний алгоритм або алгоритм оптимізації на основі переміщення бактерій, так і система, що складається з декількох алгоритмів, де алгоритми деяким чином взаємодіють між собою.

У мурашиному алгоритмі, колонія мурашок також може розглядатися як багатоагентна система, в якій кожен агент (мурашка) функціонує автономно за дуже простим правилом. На противагу майже примітивній поведінці агентів, поведінка всієї системи виходить напрочуд розумною.

Мурашині алгоритми серйозно досліджуються європейськими вченими з середини 90-х років. На сьогоднішній день вже отримані хороші результати для оптимізації таких складних комбінаторних завдань, як задача комівояжера, задача оптимізації маршрутів вантажівок, завдання розмальовки графа, квадратична задача про призначення, задача оптимізації мережевих графіків, завдання календарного планування та багато інших.

Особливо ефективні мурашині алгоритми при динамічній оптимізації процесів в розподілених нестаціонарних системах, наприклад, трафіках в телекомунікаційних мережах.

Генетичний алгоритм (ГА) сам по собі не є багатоагентною системою, але для вирішення ряду завдань є досить ефективним. В основі ГА лежать принципи природної еволюції, сформульовані Дарвіном, – природний відбір, мінливість, спадковість. З їх допомогою ГА моделюють генетичні процеси, що відбуваються в біологічних спільнотах.

Зазвичай генетичні алгоритми застосовуються для рішення оптимізаційних завдань. Предметна область ГА включає в себе проблеми комбінаторики, біоінформатики та ін. ГА застосовуються також для обробки і розпізнавання образів, зокрема зображень.

Ще один алгоритм – оптимізація на основі моделювання переміщення бактерій (BFO) був прийнятий науковим співтовариством у якості глобального алгоритму оптимізації для розподіленої оптимізації та управління. BFO грунтується на моделюванні поведінки кишкової палички. BFO вже привернув увагу дослідників через свою ефективність у вирішенні реальних завдань оптимізації, що виникають в декількох областях застосування. Біологічна основа стратегії – переміщення бактерій E.coli, емулюється дивним чином і використовується як простий алгоритм оптимізації.

Метою виконання даної наукової роботи є аналіз існуючих евристичних алгоритмів, застосовуваних у задачах розпізнавання образів. Аналіз проводиться в контексті розпізнавання форм двовимірних об'єктів, які можуть бути отримані з пристроїв, що використовують технологію multitouch.

1. Мета і завдання дослідження, плановані результати

Об'єктом дослідження є бінарне зображення.

Предметом дослідження є еволюційний метод пошуку форм двовимірних об'єктів на заданому зображенні.

Основним завданням є дослідження, розробка і програмна реалізація еволюційного методу пошуку форм двовимірних об'єктів на бінарному зображенні.

2. Актуальність теми

Розпізнавання простих геометричних фігур на зображеннях дуже поширене в ряді завдань, тому що такі фігури часто присутні в середовищі, створеному людиною. Для цього завдання останнім часом відкрилася ще одна область – мобільні сенсорні пристрої. У деяких додатках і іграх потрібно розпізнавати примітивні фігури, зчитувані з екрану в результаті проведення по ньому маніпулятором.

3. Передбачувана наукова новизна

Передбачається, що швидкість пошуку при роботі розробленого методу або розробленої модифікації існуючого методу буде вище, ніж у методів поширених на даний момент, за рахунок виконання тільки однієї ітерації пошуку.

4. Огляд існуючих методів розпізнавання

Одним з найпоширеніших серед детермінованих методів є метод перетворень Хафа (HT), який часто вимагає об'ємних обчислень і витрат пам'яті. Щоб подолати ці обмеження, дослідники запропонували нові підходи до HT, наприклад, імовірнісний HT, рандомізований HT і нечіткий HT. Ефективність використання перетворень Хафа різко падає при збільшенні розмірності фазового простору. Перетворення Хафа можна застосувати для будь-якої фігури, форма якої повністю визначається деяким набором параметрів, наприклад прямокутника, трикутника, і т.д [1]

Як альтернатива заснованим на HT методам, задача розпізнавання форми вирішувалася методами стохастичного пошуку. Стохастичні алгоритми, подібно генетичним алгоритмам (GA),показують хороші результати пошуку оптимальних рішень через володіння великою кількістю неявного паралелізму.

У 2002 році був запропонований потужний алгоритм оптимізації, тепер відомий як алгоритм оптимізації, заснований на пересуванні бактерій(BFOA). Він являє собою багатоагентну систему. BFOA імітує окрему і згруповану поведінку бактерій, що живуть в кишечнику більшості ссавців. За допомогою цього алгоритму існує можливість виявляти форми, якщо адаптувати його для цього завдання.

Для задачі розпізнавання простих фігур обраний алгоритм BFOA, так як для знаходження їм різних фігур досить замінити функцію визначення оптимальності особини і залежно від фігури буде змінено простір пошуку.

5. Опис роботи алгоритму BFOA для розпізнавання кола

Кожне ймовірне коло представлене позицією бактерії, де перші два компоненти вектора, х і у – координати центру цього кола, а третій компонент r – радіус.

Нехай (x_k,y_k,r_k) буде k-м тестовым колом популяції, де k = 1,…,S, де S – це розмір популяції, тобто позначає загальну кількість тестових кіл. У фазі ініціалізації випадкові значення в підходящому діапазоні присвоєні кожній з трьох координат векторів. Давайте розглядати 2N рівномірно розподілених демонстраційних точок на колі. На рис. 5 показаний випадок, колиN=4.

Припустимо, що бажане коло розташовуєтьсяна деякому зображенні. Функція P(x,y) дорівнює 1, якщо піксель (x,y) є граничним, 0 – інакше. Нехай A буде граничною матрицею. Цільову функцію позначимо як J. Нехай для (x₀,y₀,r₀) тестового кола її значення буде J₀ = J(A, x₀, y₀, r₀).

Рисунок 5.1 – Коло з демонстраційними точками, зображеними синім (анімація: 4 кадри, 7 циклів повторення, 95 кілобайт)

 

Для визначення чи є кандидат колом можна розглянути множину кіл з центром в (x₀,y₀) і радіусом, що варіюється в діапазоні від  до . Назвемо цю множину тестовою смугою. Значення  можна взяти як відсоток від радіуса, пропонується . Після цього N тестових точок беруться для кожного кола в тестовому діапазоні. Тестові точки розташовані на колі на рівній відстані один від одного. Нехай i-я тестова точка на тестовому колі має радіус  і позначається .

          (5.1)

Рисунок 5.2 – Формула обчислення x для i-ої тестової точки

          (5.2)

Рисунок 5.3 – Формула обчислення y для i-ої тестової точки

де i = 1,2,…,N; j = -,,…0…,,.

Щоб виміряти ступінь приналежності тестової точки до кола центрального кола визначимо функцію відстані . Значення функції відстані  для тестової точки  визначається як:

          (5.3)

Рисунок 5.4 – Формула обчислення функції відстані для i-ої тестової точки

Значення  може змінюватися в діапазоні від 0 до 1. Коли , це значить, що вибрана точка гранична і вона знаходиться на центральному колі. Якщо  не гранична точка то .

Цільова функція, яка відповідає (x₀,y₀,r₀) для граничної матриці A визначається за наступною формулою

          (5.4)

Рисунок 5.5 – Формула обчислення цільової функції

Цільова функція зважує кожну граничну точку згідно радіусу кола кандидата [3].

Таким чином, стає можливим за допомогою алгоритму BFOA розпізнати коло на зображенні. Аналогічним чином можна підібрати параметри, які ідентифікують будь-яку іншу фігуру, визначити відповідну цій фігурі цільову функцію і наведений алгоритм можна буде використовувати для пошуку цієї фігури на зображенні.

6. Існуюча модифікація для знаходження декількох фігур на одному зображенні

Запропонований алгоритм з деякими модифікаціями може виявляти безліч фігур на одному зображенні. Цього можна досягти, якщо задати верхню межу числа фігур. Метод виконується на вихідній граничній карті. Коли фігура знайдена – вона маскується на граничній карті. Потім знову виконуємо пошук. Процедура повторюється до тих пір, поки задану кількість фігур не буде знайдено. У цьому підході є можливість помилкового виявлення в разі, якщо фактичне число фігур менше, ніж зазначена максимальна кількість [3].

7. Опис роботи алгоритму BFOA для розпізнавання довільної форми.

Уявімо бактерію позицією гаданої форми у вигляді координат х і у, її кута повороту a і масштабу s. Форма є масивом вершин відносно її положення.

Нехай (x_k,y_ka_ks_k) буде k-ої тестової формою популяції, де k = 1,…,S, а S - це розмір популяції, тобто позначає загальну кількість тестових форм. При ініціалізації кожної з чотирьох координат векторам присвоюються випадкові значення у відповідному діапазоні. Розглянемо N демонстраційних точок довільної фігури. На рис. 7.1 показаний випадок, коли N = 10 для розпізнавання трапеції.

Припустимо, що шукана форма розташовується на деякому зображенні. Функція P(x,y) рівняється 1, якщо піксель (x,y) є граничним, 0 – інакше. Нехай A буде граничної матрицею. Цільову функцію позначимо як J. Нехай для (x₀,y₀a₀s₀) тестовой формы ее значение будет J₀ = J(A, x₀, y₀, a₀, s₀).

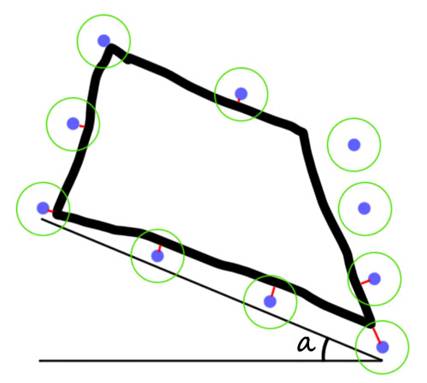
Рисунок 7.1 – Довільна форма з демонстраційними точками, зображеними синім

Для визначення чи є кандидат шуканої формою потрібно обчислити цільову функцію. Чим менше значення цільової функції, тим більш точно форма відповідає кандидату. Цільова функція обчислюється на підставі суми відстаней від тестових точок до найближчих граничним точкам, якщо такі є.

Показник r являє собою радіус кола навколо тестової точки, де буде проводитись пошук граничної точки. У загальному випадку пропонується брати його наступним чином:

,          (7.1)

Рисунок 7.2 – Формула обчислення r

де .

На рис. 7.1 зеленим зображені круги з радіусом r навколо тестових точок.

Щоб виміряти ступінь приналежності тестової точки до форми на граничній матриці, визначимо функцію відстані . Якщо існує таке k і l, що , то значення функції відстані  для i-ой тестової точки визначається як:

,          (7.2)

Рисунок 7.3 – Формула обчислення функції відстані

где .

Иначе . Також , якщо результат обчислень за формулою (7.2) більше, ніж r, де M – число більше 1. Пропонується брати .

Значення  може змінюватися в діапазоні від 0 до 1 або дорівнювати 2. Коли знаходиться в діапазоні від 0 до 1, це означає, що гранична точка знаходиться на відстані від тестової точки. Якщо , це означає, що немає граничної точки, яка лежить ближче, ніж на відстані r від тестовою.

На рис. 7.1 червоним зображені  для тестових точок.

Цільова функція, відповідна (x₀,y₀a₀s₀)для граничної матриці A визначається за наступною формулою:

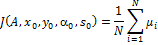          (7.3)

Рисунок 7.4 – Формула обчислення цільової функції

Таким чином, можливо розпізнавати довільні форми на зображенні.

8. Запропонована модифікація для розпізнавання декількох фігур на одному зображенні

 Пропонується альтернативний варіант знаходження декількох фігур наодному зображенні.

В якості критерію зупинки алгоритму пропонується деяка кількість ітерацій алгоритму без поліпшення сумарної цільової функції всіх особин. Кількість таких ітерацій необхідно визначити експериментально.

Розмір популяції є одним із ключових чинників цієї модифікації. Недостатній розмір популяції може призвести до того, що деякі фігури можуть бути не знайдені. З іншого боку, великий розмір популяції сильно позначиться на продуктивності алгоритму і швидкості виявлення фігур. Розмір популяції має бути визначений експериментально.

Після відпрацювання алгоритму необхідно застосувати будь-який з алгоритмів кластеризації для невідомої кількості кластерів до особин. Кожна особина з найкращим значенням цільової функції в кластері буде шуканої фігурою, якщо значення її цільової функції перевищує деякий поріг, визначений експериментально.

Висновки

Проведено огляд методів, які можуть бути застосовані для задачі розпізнавання простих фігур. Вибрано метод розпізнавання для цього завдання. Обгрунтовано причини вибору. Розглянуто роботу алгоритму BFOA на прикладі розпізнавання кола. Розглянута існуюча модифікація алгоритму BFOA для пошуку кількох фігур на зображенні. Запропонована модифікація цього методу. Проведена порівняльна характеристика існуючої та запропонованої модифікації. Надалі планується дослідження роботи існуючої та запропонованої модифікацій на різних зображеннях для визначення числових характеристик швидкості роботи, а також планується аналіз різних цільових функцій.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.

Список джерел

1.  Преобразование Хафа (Hough transform) [Електронний ресурс]. – Режим доступа : http://www.cgm.computergraphics.ru/content/view/36.

2.  Kim D.H., Abraham A., Cho J.H. A Hybrid Genetic Algorithm and Bacterial Foraging Approach for Global Optimization // Information Sciences. – 2007. – № 18 (177). – P. 3918-3937.

3.  S. Dasgupta, S. Das, A. Biswas, A. Abraham Automatic circle detection on digital images with an adaptive bacterial foraging algorithm // Soft Comput. – 2010. – P. 1151–1164.

4.  Генетический алгоритм [Електронний ресурс]. – Режим доступа : ru.wikipedia.org/wiki/Генетический_алгоритм.

5.  Neidhardt F.C., Ingraham J.L., Schaechter M. Physiology of the Bacterial Cell: A Molecular Approach. – Sunderland: Sinauer Associates, 1990. – 520 p.

6.  Alberts B., Bray D., Lewis J., Raff M., Roberts K., Watson J.D. Molecular Biology of the Cell. – New York: Garland Publishing, 1994. – 1408 p.

7.  Segall J.E., Block S.M., Berg H.C. Temporal Comparisons in Bacterial Chemotaxis // Proceedings of the National Academy of Sciences. – 1986. – № 83 (23). – P. 8987-8991.

8.  Berg H.C. Random Walks in Biology. – Princeton: Princeton University Press, 1993. – 164 p.

9.  Woodward D.E., Tyson R., Myerscough M.R., Murray J.D., Budrene E.O., Berg H.C. Spatio-Temporal Patterns Generated by Salmonella Typhimurium // Biophysical Journal. – 1995. – № 68. – P. 2181-2189.

10.  Analysis And Design of Intelligent Systems Using Soft Computing Techniques / Eds.: P. Melin, O.R. Castillo, E.G. Ramirez, J. Kacprzyk. – Heidelberg: Springer, 2007. – 855 p.

11.  Passino K.M. Biomimicry of Bacterial Foraging for Distributed Optimization and Control // IEEE Control System Magazine. – 2002. – № 3 (22). – P. 52-67.