Модели множественной регрессии

В большинстве случаев необходимо идентифицировать более одного фактора, влияющего на стоимость объекта оценки. Количественные измерения влияния множества факторов на зависимую переменную (у) можно осуществить на основе методики многофакторного регрессионного анализа. В данном случае, так же как и в парной регрессии, зависимость может характеризоваться как линейной, так и нелинейной связью. Линейная модель множественной регрессии имеет общий вид:

где

h1 b2 bn - коэффициенты множественной регрессии;
x1, x2, хn – факторы, влияющие на стоимость объекта оценки, включенные в анализ;
b0 – постоянная величина, не зависящая от влияния отобранных факторов;
n – объем статческой выборочной совокупности данных

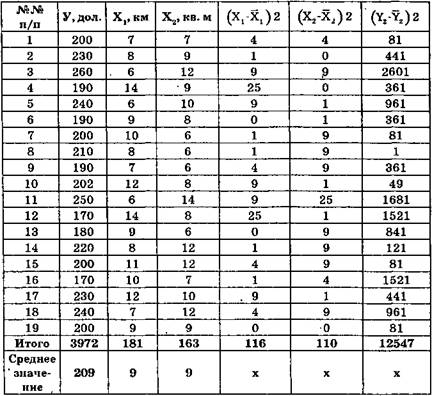
Можно исследовать линейную зависимость между у и любой комбинацией независимых переменных, однако модель будет иметь силу только в случае, если существует значимая связь и если каждый коэффициент регрессии b значимо отличается от нуля. Факторы – это технические, экономические, природно–климатические, организационные, технологические, социально–демографические и другие показатели, оказывающие количественное влияние на какой–либо результирующий экономический показатель: себестоимость, прибыль, выручка, стоимость объекта, денежный поток. Задача математического моделирования состоит в выявлении количественной связи между факторами и результирующим показателем (признак–фактором). Факторы не должны быть тесно связаны между собой, т. е. не должно быть мультиколлинеарности.Рассмотрим методику построения многофакторной регрессионной модели на примере (табл. 7.5.1). Необходимо установить закономерность влияния на стоимость 1 м2 жилья (у) двух факторов: удаленность от центра города (X1) и площадь кухни (Х2).

Таблица 7.5.1 Расчет параметров регрессионной модели

Определим парные коэффициенты корреляции:

между У и Х1;
между У и Х2;
между Х1 и Х2.

Полученные значения приведены в табл. 7.5.2. Промежуточные расчеты опускаем, так как методика такого рода вычислений рассмотрена ранее.

Таблица 7.5.2 Парные коэффициенты корреляции

На основе полученных результатов следует вычислить коэффициенты регрессии в стандартизированном виде, опираясь на следующую систему уравнений:

Решив систему уравнений, получим значения:

Коэффициенты регрессии в нормализованном виде определим по формулам:

Формулы для расчета коэффициента регрессии

где σy , σх1 , σх2 – средние квадратичные отклонения, определенные по формулам:

X1, X2, X3 –средние значения соответствующих переменных. Окончательное уравнение регрессии имеет вид:

Полученная модель указывает на то, что удаленность от центра влияет на стоимость жилья отрицательно и каждый дополнительный 1 км приведет к снижению стоимости 1 кв. м на 4,74 дол. Напротив, такой фактор как площадь кухни влияет положительно: увеличение площади на 1 кв. м ведет к росту стоимости 1 кв. м на 6,44 дол. Коэффициент множественной корреляции для данной линейной модели может быть получен по следующей формуле:

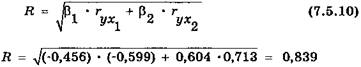
Формулы для расчета коэффициента корреляции

Коэффициент детерминации:

Коэффициент детерминации R² измеряет долю вариации у, объяснимую влиянием факторов Х1 , Х2......Хn, включенных в анализ. В данном случае эта доля составляет 0,703. Для оценки полученной модели на достоверность необходимо проверить значимость парных коэффициентов корреляции и коэффициентов регрессии каждой независимой переменной. Формула t–критерия Стьюдента:

где (n – 2) – число степеней свободы. Критерий следует определить для каждой пары, образованной зависимой переменной с каждой независимой переменной. В нашем примере n = 19; r – парный коэффициент корреляции.

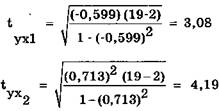
Критические значения t–критериев для уровня значимости 0,025 составляет 2,1098. Рассчитанные нами значения выше (3,08 и 4,19), что дает основание предположить, что парные коэффициенты корреляции между указанными показателями в генеральной совокупности не равны нулю и указанная линейная связь действительно существует. Оценим общую значимость полученной многофакторной модели, применив F–критерий Фишера, который определим по формуле:

где

Yi – значения независимой переменной, рассчитанные на основе модели множественной регрессии;
У – среднее значение переменной;
Уi – статистические значения переменной.

Данные получены расчетным путем на основе табл. 7.5.1. df^{регресс.} – число степеней свободы для регрессии с числом независимых переменных «k», числом данных в совокупности «n». В нашем примере:

Из таблиц стандартного распределения F–критерия получим его значение для следующих параметров:
уровень значимости = 0,05
k = 2
n-1-k=16
F–критерий = 1/19,43 = 0,051. Расчетное значение F =2,104 > 0,051, что свидетельствует о том, что полученная нами модель имеет высокую достоверность. Проверим каждое из значений коэффициентов регрессии b1 и b2. Граничные значения t–критерия при 5 % уровне, значимости при (n-1-k) степенях свободы следующие:

Значение t–критерия:

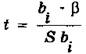
Значение t–критерия для каждого коэффициента регрессии должно лежать вне указанных границ.

Β = 0, если проверяем гипотезу, что между параметрами нет связи и X не помогает в прогнозировании У;
Β = 1, если выдвигается обратная гипотеза (в нашем примере Β=0);
bi – значение коэффициента регрессии;
S bi – стандартная ошибка bi.

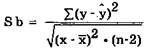
Расчетно получили следующие значения на основе информации, приведенной в табл. 7.5.1.