ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Завдання візуалізації об'єктів n-мірного простору знаходять застосування в системах управління технологічними процесами, в системах діагностики і розпізнавання образів, експертних системах і системах прийняття рішень в техніці, економіці та медицині, в лінгвістиці та психології. Останнім часом широкого поширення набули інтерактивні системи прийняття рішень, в яких відповідальна особа приймає рішення і оцінює їх наслідки на основі візуалізованих даних. [9].

Впровадження в науку і промисловість комп'ютерних томографів, незалежно від їх конструкції і фізичних принципів отримання зображення, дає можливість отримання цифрових фотографій для подальшого аналізу стану досліджуваного об'єкта, зокрема, в медицині. Але набір таких фотографій або слайдів не дозволяє досліднику приймати рішення достатньо оперативно, оскільки не дає всієї повноти інформації. Кожен слайд представляє собою піксельний поле фіксованих розмірів, визначених конструкцією томографа, кожного пікселя ставиться у відповідність атрибут, що характеризує колір, градацію кольору або яку-небудь іншу фізичну величину. Таким чином, виникає задача отримання зображень досліджуваного просторового об'єкта по цифрових фотографій (кольоровим або монохромним) у системах комп'ютерної геометрії та графіки.

Проблема візуалізації даних, отриманих з плоских паралельних перерізів просторового об'єкта, може бути вирішена за наступною схемою: синтез моделі 3D об'єкту за його 2D перетинах і отримання синтезованої моделі проекційного зображення при довільному апараті проеціювання, в тому числі стерео проеціювання.

1. Постановка проблеми

Проблема візуалізації 3D-об'єктів, які можуть бути задані різними способами, виникає в багатьох областях математики, фізики, медицини [1]:

  1. Візуалізація експериментальних даних. Наприклад, інформації, зібраної з різних датчиків, сенсорних мереж, результатів вимірювань, результатів імітаційного моделювання.
  2. Візуалізація функціонального подання. Візуалізація складних тривимірних об'єктів в математиці, візуалізація аналітично заданих поверхонь і т.п.
  3. Візуалізація медичних наборів даних. Одним з широко використовуваних методів діагностики є томографія. Томографи, що працюють на рентгенівському принципі (комп'ютерна томографія, далі КТ) і на магнітно-резонансному принципі (далі МРТ) дозволяють отримати зображення безлічі перетинів тіла пацієнта вздовж якої-небудь осі, які дають багато інформації про особливості його анатомії і фізіології. Методи візуалізації дозволяють реконструювати тривимірну структуру органів по безлічі паралельних перерізів. Візуалізація всього набору даних в даний час реалізована в програмному забезпеченні більшості сучасних томографів, але завдання виділення тривимірних областей, візуалізації області інтересу, заданої набором контурів на зрізах, візуалізація області при радіологічному лікуванні пацієнтів, як правило, в цьому програмному забезпеченні не реалізовані.
  4. Візуалізація експериментальних і модельних даних, з інших областей, таких як динаміка рідин, геологія, метеорологія, молекулярний аналіз.

Основне завдання візуалізації 3D-об'єктів формулюється так - необхідно знайти оптимальну апроксимацію для невідомої поверхні так, щоб мінімізувати похибку вимірювання, що виникає через обмеження по точності у вимірювальних приладах або через недостатню якість поверхні фізичної моделі.

Відмінною рисою всіх алгоритмів візуалізації об'єктів є їх виняткова ресурсомісткість, обумовлена необхідністю обробки великої кількості однотипних даних, тому підвищення продуктивності реалізації таких алгоритмів є актуальним завданням.

2. Аналіз літератури

Для візуалізації об'єктів, що мають велике число ознак у вигляді сукупності параметрів, на площині існує безліч методів. [9].

В даний час існують наступні класи візуалізації даних: візуалізація поверхні (surface rendering), об'ємна візуалізація (volume rendering) і гібридна візуалізація (hybrid rendering).

Алгоритми візуалізації поверхні (surface rendering) будують зображення поверхні в тривимірному просторі (одним з уявлень поверхні є рівняння, де - заданий рівень). Спочатку вихідна поверхня апроксимується полігонами, потім проводиться візуалізація полігонів за допомогою однієї з графічних бібліотек. [10].

Алгоритми об'ємної візуалізації (volume rendering) використовуються для представлення повної картини з урахуванням всіх навколишніх об'єктів. Існує чотири типи алгоритмів об'ємної візуалізації: випускання променів, розкладання на шари зі зрушує деформацією, проектування вокселів, відображення текстури.[11].

При хірургічних планування операцій на віртуальному пацієнті і в аеродинамічних симуляторах використовується гібридна візуалізація (hybrid rendering), за допомогою якої будується зображення тривимірного об'єкту (представленого тріангуляцією), вкладеного в напівпрозорий обсяг. [13].

Основними алгоритмами, які застосовуються при відновленні поверхонь, є:

  1. Алгоритми відкидання променів [2];
  2. аАлгоритми тріангуляції [3];
  3. Алгоритм марширують кубів [4];

Алгоритми відкидання променів вже досить добре вивчені, і як показали наявні на ринку вільного і комерційного ПЗ реалізації, добре распараллелен з використанням OpenGL і мови шейдеров. Такі реалізації дозволяють цим алгоритмам працювати в режимі реального часу навіть на не дуже потужних робочих станціях.

Алгоритми тріангуляції менш ресурсомісткі, при цьому маються швидкі навіть у однопотоковому варіанті реалізації. Одним із прикладів такої реалізації є алгоритм побудови тріангуляції Делоне, описаний в роботі [5], який на персональному комп'ютері середньої потужності (Core2Quad 2,83 ГГц, 8Гб ОЗП) дозволяє виконати тріангуляцію поверхні з 100000 точок за 8 секунд.

Більш ресурсоємним і менш оптимізованим є алгоритм маршируючих кубів [4],який, тим не менш, цікавий для завдань інтерактивного та автоматичного відновлення поверхонь об'єктів, представлених хмарою точок, а також для побудови опуклих оболонок. Тому в роботі розглядатимуться шляхи підвищення продуктивності саме даного алгоритму за рахунок розпаралелювання.

3. Огляд методу тріангуляції

На практиці найбільш часто проводиться розбиття зображень на трикутники.

Це пояснюється такими причинами:

  1. трикутник є найпростішим полігоном, вершини якого однозначно задають грань;
  2. будь-яку область можна гарантовано розбити на трикутники;
  3. обчислювальна складність алгоритмів розбиття на трикутники істотно менше, ніж при використанні інших полігонів;
  4. реалізація процедур рендеринга найбільш проста для області, обмеженої трикутником;
  5. для трикутника легко визначити три його найближчих сусіда, що мають з ним спільні грані.

Процес розбиття полігональної області зі складною конфігурацією в набір трикутників називається тріангуляції. При аналізі або синтезі складних поверхонь їх апроксимують сіткою трикутників, і згодом оперують з найпростішими полігональними областями, тобто з кожним з трикутників. На практиці застосовують безліч алгоритмів тріангуляції, один з них зображений на рисунку 1.

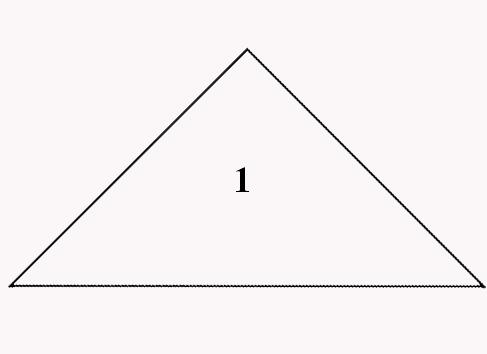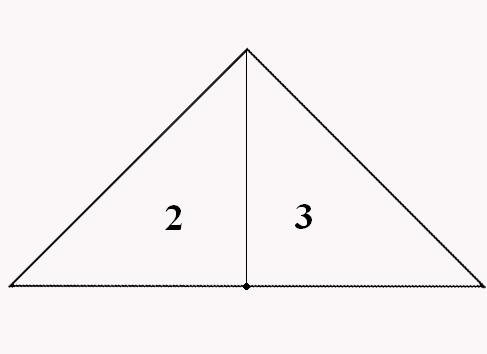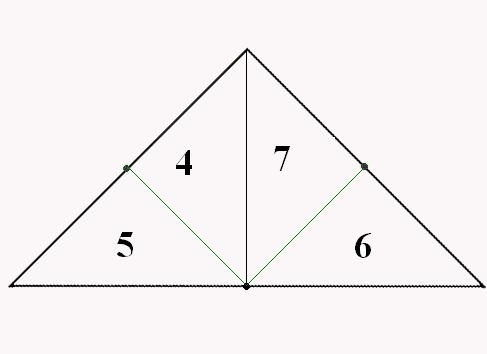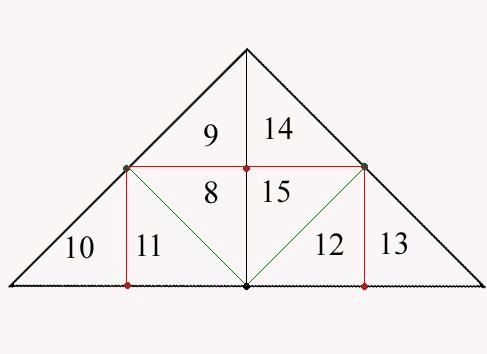
Итеративная бисекция основания

Рисунок 1 - Візуалізація 3-х ітерацій бісекції підстави трикутника алгоритму ROAM.
(анімація: 7 кадрів, 5 циклів повторения, 146 кілобайт)

Особливий інтерес до алгоритмів тріангуляції визначається тим, що вони використовуються в багатьох процедурах машинної графіки, таких як формування поверхонь, зафарбування, видалення невидимих частин, відсікання.

Будь-яка поверхня може бути апроксимована з необхідною точністю сіткою трикутників. Точність апроксимації визначається кількістю трикутників і способом їх вибору. Для якісної візуалізації об'єкту, що знаходиться поблизу точки спостереження, потрібно врахувати у багато разів більше трикутників, ніж у ситуації, коли той же об'єкт розташований на видаленні. Навіть досить груба сітка корисна на практиці, так як методи згладжування, застосовувані в процесі відображення, можуть значно поліпшити уявлення про кривизну поверхні.[12].

4. Опис алгоритму

Згідно [4], алгоритм складається з двох основних стадій. Перша стадія: побудова неявної функції F: D->R, де D належить R3 -околиця поверхні. Функція F являє собою оцінку відстані від будь-якої точки з D до поверхні. Друга стадія: тріангуляція поверхні нульового рівня функції F за допомогою алгоритму марширують кубів.

Для побудови оцінки відстані ми, асоціюємо з кожною точкою набору {x1,…,xn} орієнтовану дотичну площину Tp(xi) , яку можна знайти за допомогою методу головних компонент, застосованого до k найближчих сусідів точки xi. Обчислення функції відстані здійснюється за формулою:

F(p) = (p-oi)ni ,                (1)

де oi – найближчий до p «центр» дотичної площини (центроид k найближчих сусідів), а ni- його нормаль.

Алгоритм «марширують куби», можна розбити на два етапи:

1. Розбиття області G простору R3 на кінцевий безліч осередків, пошук осередків пересікаються шуканої поверхнею.

2. Апроксимація поверхні в знайдених осередках.

Дві ці підзадачі є незалежними. Розглянемо їх докладніше.

Перший этап.

Основні проблеми цього етапу полягає в наступному [4]:

1. Розбити область G на клітинки.

2. Вибрати осередки, які перетинаються з шуканої поверхнею.

Після того як область G буде розбита на клітинки, значення функції, в загальному випадку, яка задає поверхню будуть відомі тільки у вершинах цих осередків. Таким чином, осередок є головною структурною одиницею в усіх алгоритмах, на цьому етапі.

У тих завданнях, в яких функція, що задає поверхню, задана таблицею на регулярній сітці, проблема розбиття області G на клітинки відразу відпадає, зважаючи однозначності її вирішення - осередок повинна бути параллелепипедом - для того, щоб знати значення функції в вершинах осередку. Якщо ж функція задана явно, то осередок можна вибрати довільної форми і розміру. Проте слід врахувати деякі проблеми пов'язані з апроксимацією шуканої поверхні в комірці. Якщо розмір осередку буде дуже великим, то можлива велика втрата точності.

При великому розмірі осередку деякі частини шуканої поверхні не будуть видні. Однак вибирати комірки дуже маленького розміру не дуже добре з точки зору швидкодії. Тому розмір осередку треба вибирати не менше допустимої похибки побудови шуканої поверхні.

Форма осередку в алгоритмі «маршируючих кубів» - паралелепіпед. Однак це не єдино можливий варіант. Форма осередку визначає подальшу тріангуляцію осередки. Причому, якщо вершина осередку знаходиться поза обсягу обмеженого шуканої поверхнею, то значення цього біта 0, інакше - 1. Тоді кількість різних типів тріангуляції буде 2N. Звідси видно, що використовувати як осередки, наприклад, ікосаедр не оптимальне.

Отже, припустимо, що область G вже розбита на клітинки. Тоді головною проблемою стає пошук осередків пересікаються шуканої поверхнею. Нехай С - безліч осередків, тоді Cv - безліч осередків пересікаються поверхнею F (P) = v. Тоді можна вважати, що поверхня перетинає клітинку, якщо існують такі P1 і P2 - вершини осередку, що:

   F(p1) <v< F(p2),                                      (2)

Ця умова виконується, коли виконується:

   Mini F(pi) <v< Maxj F(pj),                                (3)

де pi та pj  – вершини осередку.

Таким чином, проблема звелася до наступного: з безлічі осередків C вибрати підмножина Cv осередків, які відповідають умові (3).

Другий етап. Простір розбивається на клітинки, і відбираються тільки ті осередки, у яких треба виробляти апроксимацію. Таким чином, завданням другого етапу є апроксимація поверхні в одній клітинці. Найбільш оптимальний спосіб апроксимації - тріангуляція [4].

Необхідно визначити, скільки способів тріангуляції має паралелепіпед. Нехай є 8-бітовий індекс. Тоді зіставимо кожній вершині один біт в індексі. Причому, якщо вершина осередку знаходиться поза обсягу обмеженого шуканої поверхнею, то значення цього біта 0, інакше - 1. Тоді кількість різних типів тріангуляції буде 28=256.

Отримавши спосіб тріангуляції, можна вже апроксимувати поверхню в комірці. До цього моменту вже відомо кількість трикутників, а для кожного трикутника відомі ребра осередків, на яких лежать його вершини. Залишається знайти точку на ребрі осередку, в якій поверхня її перетинає.

5. Застосування розпаралелювання

Как видно из алгоритма марширующих кубов, он содержит много этапов, на которых выполняются независимые задачи. Наличие независимых задач является достаточным условием для распараллеливания алгоритма. К ним относятся:

обчислення ідентифікаторів точок;

перевпорядочення точок;

виділення вокселів сітки;

обчислення шаблонів осередків;

генерація трикутників.

Так як ці завдання припускають однотипні операції над великою кількістю даних, то распараллеліть їх було б досить добре, використовуючи навіть обчислювальні системи, що відносяться до класу SIMD. До таких систем відносяться сучасні графічні прискорювачі [6]. Для найбільш універсального прискорення розрахунків з використанням GPGPU пропонується варіант розпаралелювання алгоритму із застосуванням OpenCL, що дозволить застосовувати прискорювачі nVidia, AMD і Intel. Використання графічних прискорювачів при вирішенні даної задачі аргументується тим, що виконання розрахунків з використанням графічного ядра дає хороші результати в алгоритмах, що використовують паралельну обробку великих масивів даних. У нашому випадку відношення числа арифметичних інструкцій, які доведеться виконувати при побудові поверхні, досить велике по відношенню до числа звернень до пам'яті, що зазвичай дає кращі результати при реалізації із застосуванням GPGPU обчислень.

Алгоритм повинен містити наступні кроки:

  1. Реалізація прискорюючої структури, для вхідного набору даних.
  2. Відновлення поля нормалей.
  3. Обчислення оцінки відстані.
  4. Знаходження поверхні нульового рівня оцінки відстані (алгоритм «марширують кубів»).

На першому кроці в якості прискорюючої структури пропонується використовувати регулярну сітку. Паралельна побудова регулярної сітки складається з п'яти етапів: побудова обмежує паралелепіпеда, обчислення ідентифікаторів точок, сортування ідентифікаторів точок, переупорядочивание точок, виділення вокселів сітки. У підсумку, в пам'яті будуть зберігатися тільки ті вокселі, які містять точки даних, що дозволяє значно знизити використання відеопам'яті.

На другому кроці, необхідно знайти дотичну площині для кожної з точок вхідних даних.

Хороша реалізація паралельного алгоритму пошуку дотичній наведена в роботі [7]:

  1. Отримати з глобальної пам'яті оброблювану точку.
  2. Визначити цілочисельні координати вокселя (x, y, z).
  3. Виконати вибірку індексів точок вокселя (x, y, z) і його сусідів.
  4. Скопіювати точки з отриманими індексами в локальну пам'ять і відсортувати крапки по зростанню відстані.
  5. Вибрати з локальної пам'яті координати найближчих точок.
  6. Обчислити центроид і помістити його у вихідний буфер.
  7. Обчислити матрицю коваріації для обраних точок, знайти мінімальне власне число і помістити відповідний йому власний вектор у вихідний буфер.

Для обчислення оцінки відстані пропонується поміщати центроїди в прискорюючу структуру, що дозволяє використовувати таку паралельну схему:

  • Отримати з глобальної пам'яті оброблювану точку.
  • Визначити цілочисельні координати вокселя (x, y, z).
  • Знайти найближчий центроид і відповідну йому нормаль.
  • Обчислити оцінку відстані.

    • Алгоритм марширують кубів, розпаралелених з використанням OpenCL, складається з наступних кроків: обчислення шаблонів осередків; обчислення адрес вершинного буфера; генерація трикутників. Така техніка дозволяє отримати вихідні дані різної довжини від кожного потоку в один буфер паралельно.

    Слід зазначити, що, незважаючи на свою популярність і широке застосування, алгоритм марширують кубів має істотний недолік: на досить простих ділянках поверхні він виконує дуже велику кількість поділів. Наприклад, на поверхні, яка може бути апроксимована за допомогою 440 полігонів, класичний алгоритм може згенерувати порядку 67000 [8]. Це підкреслює виграш в продуктивності від розпаралелювання, але також говорить про необхідність поліпшення базового алгоритму.

    Висновок

    У результаті роботи показано, що завдання підвищення продуктивності методів, реконструюють і візуалізуючих поверхню, є актуальною. Показано, що мета може бути досягнута за рахунок вирішення завдання розпаралелювання алгоритмів, застосовуваних у реалізації цих методів. Наведено обгрунтування, що доцільно вирішити, в першу чергу, завдання розпаралелювання алгоритму «марширують кубів». Виявлено, що алгоритм може бути ефективно распараллелен із застосуванням GPGPU обчислень. Наведено паралельний алгоритм, реалізований з використанням OpenCL.

    Перелік посилань

    1. Сравнительный анализ методов интерактивной триангуляции сеточных функций/ Интернет-ресурс. - Режим доступа: www/URL:http://cgm.computergraphics.ru/content/view/63#_.
    2. Volume ray casting / Интернет-ресурс. – Режим доступа: www/URL: http://en.wikipedia.org/wiki/Volume_ray_casting
    3. А. В. Скворцов Триангуляция Делоне и её применение. – Томск: Изд-во Томского ун-та, 2002. – 128с.
    4. Lorensen, W. E., And Cline, H. E. 1987. Marching cubes: A highresolution 3d surface construction algorithm. In Proceedings of SIG-GRAPH’87, 163–169.
    5. V. Domiter, B. Zalik Sweep-line algorithm for constrained Delaunay triangulation / Int. Journal of Geographical Information Science, Vol. 22, No. 4, April 2008. – P. 449-462.
    6. NVIDIA Corporation. NVIDIA CUDA Compute Uni?ed Device Architecture Programming Guide. Version 3.2.2010.
    7. GPU-алгоритм восстановления поверхности из облака точек/Интернет-ресурс.-URL:http://nano.msu.ru/files/conferences/GPU-2010-05/abstracts.pdf
    8. S. Schaefer, J. Warren, Dual Marching Cubes: Primal Contouring of Dual Grids / PG '04 Proceedings of the Computer Graphics and Applications, 12th Pacific Conference, 2004. – P.70-76.
    9. Научная библиотека диссертаций и авторефератов disserCat. Интернет-ресурс. - Режим доступа: www/URL: http://www.dissercat.com/content/metod-i-ustroistvo-vizualizatsii-prostranstvenno-raspredelennykh-obrazov-so-slozhnymi-topolo#ixzz2XKkRwcKZ.
    10. Визуализация данных поверхности. Интернет-ресурс. - Режим доступа: www/URL: http://docs.autodesk.com/CIV3D/2013/RUS/index.html?url=filesCTU/GUID-58270E7F-E5E0-4196-B194-4965255695F6.htm,topicNumber=CTUd30e10204.
    11. Гаврилов Н.И. Организация потоковых вычислений на GPU для интерактивной визуализации медицинских объемных данных. Интернет-ресурс. - Режим доступа: www/URL: http://escience.ifmo.ru/cms/content/Gavrilov.pdf
    12. Романюк Александр, Сторчак Александр Алгоритмы триангуляции Интернет-ресурс. - Режим доступа: www/URL:http://thalion.kiev.ua/idx.php/4/249/article
    13. Бугров Н.В., Голубев В.И., Дижевский А.Ю., Какауридзе Д.Г., Клименко А.С., Обоймов А.С., Фролов П.В. Обзор алгоритмов гибридной визуализации поверхности, вложенной в полупрозрачный объем Интернет-ресурс. - Режим доступа: www/URL: https://googledrive.com/host/0B8dxsp-U3fIiRnc5WEpmTThQRVU/MEDIAS2012-22-FrolovPV-Tomo3D.pdf