в библиотеку

Перевод с английского языка: Селиванова А.И.

Алгоритм решения проблемы нечеткого максимального потока с использованием обобщенных треугольных нечетких чисел

Авторы: Амит Кумар и Манджот Каур
Школа математики и компьютерных приложений, университет Tхапар, Патиала, Индия

Источник: iospress.metapress.com/content/071447068444w215/fulltext.pdf

Аннотация: Есть несколько статей по литературе, в которых обобщенные нечеткие числа используются для решения реальных проблем жизни, но в меру наших знаний, до настоящего времени никто не использовал обобщенные нечеткие числа для решения проблемы максимального потока. В данной работе, существующий алгоритм изменен, чтобы найти нечеткий максимальный поток между источником и приемником, представляя все параметры как обобщенные треугольные нечеткие числа. Чтобы проиллюстрировать модифицированный алгоритм, был решен числовой пример, и полученные результаты были сравнены с существующими результатами. Если нет никакой неопределенности в отношении потока между источником и приемником, то предложенный алгоритм дает тот же результат, что и в максимальной четкой проблеме потока.

Введение

Задача о максимальном потоке является одной из основных проблем для комбинаторной оптимизации в весовых ориентированных графах. Это дает очень полезные модели в ряде практических задач включая сети связи, системы нефтепроводов и энергетических систем. Максимальный поток проблемы и ее вариации имеют широкий спектр применения и хорошо изучены. Задача о максимальном потоке была предложена Фалкерсоном и Данцигом, и решена специализирующимся симплекс-методом для линейного программирования. Форд и Фалкерсон решили ее путем увеличения пути алгоритма. Существуют эффективные алгоритмы для решения проблем четкого максимального потока.

1.1. Обзор проблем нечеткого максимального потока.

В реальной жизни всегда существуют неопределенности в параметрах (например, затраты, возможности и требования) проблем максимального потока. Чтобы справиться с таким типом проблем, параметры проблем максимального потока представлены нечеткими числами максимальным потоком проблемы с нечеткими параметрами. В литературе, число работ, посвященных нечеткой максимальной проблеме потока меньше. Книга Кима и Роуша является одной из первых на эту тему. Авторы разработали теории нечетких потоков, предоставив условия для получения оптимального потока, с помощью определений нечетких матриц. Но были и Колодзиоужик и Шана, которые представили основные работы в литературе с участием этой темы. Они приблизились к этой проблеме, используя минимальную технику сокращений.

В первой статье, Шана и Колодзиоужик предложили алгоритм для графа с четкой структурой и нечеткими мощностями, т. е. дуги имеют функцию принадлежности связанную в их потоке. Эта проблема изучалась Шаном и Kolodziejczyk еще раз, в этой статье поток - действительное число, и у мощностей есть верхние и более низкие границы с функцией удовлетворения. Шана и Kolodziejczyk также изучили поток целого числа и предложили алгоритм. Шана и др. изучили проблему максимального потока, когда основная связанная структура плохо определена и должна быть смоделирована как нечеткий граф. Ши и Ли предложили прикладные линейные программные алгоритмы, чтобы решить нечеткие многоуровневые проблемы минимального потока стоимости с нечеткой стоимостью, с учетом разной степени достоверности. Даймонд разработал ценную версию интервала от максимального потока к минимальному сокращению теоремы и алгоритм Карпа-Эдмондса, обеспечивающего надежность оценки потоков в неточных сетях или неопределенных условиях. Эти результаты распространяются на сети с нечеткими мощностями и потоками.

Лю и Као исследовали сетевые проблемы потока, решив что длины дуги сети - нечеткие числа. Джи и др. рассмотрели обобщенную нечеткую версию проблемы максимального потока, в которой мощности дуги - нечеткие переменные. Эрнандес и др. предложили алгоритм, основанный на классическом алгоритме Форда - Фалкерсона. Алгоритм использует технику возрастающего графа, представляющий все параметры как нечеткие числа. Гэти и Хашеми исследовали полностью нечеткую проблему минимального потока стоимости, рассматривая большое разнообразие ранжирования функций. Гэти и Хашеми представили некоторые различные случаи нечеткой минимальной проблемы потока стоимости, использующей полный заказ и номинальные потоки. Гэти и Хашеми предложили новый подход к решению многоцелевой проблемы полностью нечеткого минимального расхода стоимости потока с нечеткими величинами и нечеткими отношениями. Кумар и др. предложили новый алгоритм поиска нечеткого максимального потока между источником и вкладом с помощью функции ранжирования.

1.2. Важность обобщенных нечетких чисел

Рейтинг нечетких чисел играет важную роль в процессе принятии решений. Нечеткие числа должны быть упорядочены до каких либо действий осуществляемых лицами, принимающими решения. Джайн была предложена концепция классификации функции для сравнения нормальных нечетких чисел. Чен отметил, что во многих случаях это не возможно, ограничить функции принадлежности к нормальной форме и предложил концепцию обобщенных нечетких чисел. С тех пор тратятся огромные усилия чтобы добиться значительных успехов, но виден значительный прогресс в развитии многочисленных методов для классификации обобщенных нечетких чисел.

В большинстве работ обобщенные нечеткие числа превращаются в нормальные нечеткие числа посредством процесса нормализации, а затем нормальные нечеткие числа используются для решения реальных жизненных проблем. Кауфман и Гупта отметили, что существуют серьезные расхождения процесса нормализации. В основном мы преобразовывали измерения объективной ценности для оценки субъективной ценности, что приводит к потере информации. Хотя эта процедура является математически правильной, это уменьшает количество информации, которая доступна в исходных данных, и мы должны избежать этого.

Се и Чен отметили, что арифметические операции над нечеткими числами, представленные Ченом не только изменяют тип функции принадлежности нечетких чисел после арифметических операций, но и могут также уменьшить сложность и скучность арифметических операций.

Есть несколько работ, в которых обобщенные нечеткие числа используют для решения реальных жизненных проблем, но в меру наших знаний, до сих пор никто не использовал обобщенных нечетких чисел для решения проблемы максимального потока.

1.3. Вклад данной работы

В этой статье, существующий алгоритм изменен, чтобы найти нечеткий максимальный поток между источником и вкладом, представляя все параметры как обобщенные треугольные нечеткие числа вместо нормальных нечетких чисел. Чтобы проиллюстрировать измененный алгоритм,решен числовой пример, и полученные результаты были сравнены с существующими результатами. Если нет никакой неуверенности по поводу потока между источником и вкладом тогда, предложенный алгоритм дает тот же результат, что и в максимальной четкой проблеме потока.

1.4. Структура работы

Данная работа организована следующим образом: в разделе 2, основные определения, арифметические операции, функция ранжирования и метод, для нахождения минимума и максимума двух обобщенных треугольных нечетких чисел. В разделе 3 алгоритм для решения проблемы нечеткого максимального потока. В разделе 4 для иллюстрации предложенного алгоритма решен числовой пример. Полученные результаты обсуждаются в разделе 5 и выводы обсуждаются в разделе 6.

5. Результаты и обсуждение

В этом разделе обсуждаются преимущества предложенного алгоритма и результаты существующего алгоритма, а также их сравнение.

5.1. Преимущества предлагаемого алгоритма по сравнению с существующими алгоритмами

Существующий алгоритм может быть применен, только если все параметры задачи о максимальном потоке представлены нормальными нечеткими числами. Пока предлагаемый алгоритм может применяться в следующих трех случаях:
1.5. Если все параметры представлены обобщенными нечеткими числами.
1.6. Если все параметры представлены нормальными нечеткими числами.
(III) Если некоторые параметры представлены обобщенным, и некоторые представлены нормальными нечеткими числами. Если все параметры проблемы представлены обобщенными нечеткими числами то, чтобы применить существующий алгоритм, необходимо преобразовать все параметры в нормальные нечеткие числа посредством процесса нормализации. Кауфман и Гупта указали, что есть серьезное неудобство процесса нормализации. В основном мы преобразовали измерение объективной ценности к оценке субъективной ценности, которая приводит к потере информации. Хотя эта процедура математически правильна, она уменьшает количество информации, которая доступна в оригинальных данных, и мы должны избежать его. Чтобы объяснить неудобства процесса нормализации, был решен пример 3, использован существующий и предложенный алгоритм, и полученные результаты сравнены в Разделе 5.2.

5.2. Сравнение результатов

Предполагая, что все параметры (затраты, мощности и требования), представлены как обобщенные нечеткие числа, собраны от того же самого лица, принимающего решения, на основе опыта лица, принимающего решения, тогда результаты, полученные при помощи существующего алгоритма и предложенного алгоритма, обсуждены в разделах 5.2.1 и 5.2.2.

5.2.1. Результаты существующего алгоритма

Если все важные параметры, используемые в Примере 3, сначала нормализованы, то проблема решена при помощи существующего алгоритма, значит нечеткий оптимальный поток F = (0, 60, 120; 1).

Полученный результат может быть объяснен следующим образом:
(i) Согласно лицу, принимающему решения, количество потока между источником и вкладом больше, чем 0 и меньше чем 120 единиц.
(ii) лицо, принимающее решения принимает его 100% в пользу того, что максимальное количество потоков будет равно 60 единиц.
(iii) процент в пользу лица, принимающего решения, для остающегося количества потока может быть получен следующим образом:
Пусть х представляет собой сумму потоков, значит процент в пользу лица, принимающего решение для

5.2.2. Результаты предложенного алгоритма

Если важные параметры того же самого примера не нормализованы, то проблема решена при помощи предложенного алгоритма, значит нечеткий оптимальный поток F = (0, 60, 120; 2).

Полученные результаты могут быть объяснены следующим образом:
(i) согласно лицу, принимающему решения, количество потока между источником и вкладом больше, чем 0 и меньше чем 120 единиц.
(ii) решение на 20% в пользу того, что максимальное количество потоков будет равно 60 единиц.
(iii) процент в пользу лица, принимающего решения, для остающегося количества потока может быть получен следующим образом:
Пусть х представляет собой сумму потоков, значит процент в пользу лица, принимающего решение для

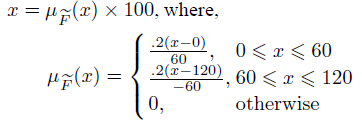
Это очевидно из результатов, объясненных в Разделах 5.2.1 и 5.2.2, что согласно лицу, принимающему решения, количество максимального потока то же самое в обоих случаях. То есть, максимальный поток будет больше, чем 0 единиц и меньше чем 120 единиц, но в связи с процессом нормализации фактический процент для разного количества максимального потока изменяется.

Например: Результаты с процессом нормализации представляют, что количество максимального потока будет составлять 60 единиц на 100% , в то время как без нормализации процесса на ту же сумму составляет 20%.

Следовательно, лучше использовать обобщенные нечеткие числа вместо нормальных нечетких чисел, полученных при помощи процесса нормализации.

6. Заключения

В этой статье алгоритм предложен для того, чтобы найти нечеткий оптимальный поток проблем нечеткого максимального потока, в которых потоки представлены обобщенными нечеткими числами. Числовой пример решен, чтобы проиллюстрировать предложенный алгоритм. Предложенный алгоритм очень легко понять и применять для решения проблем нечеткого максимального потока, происходящих в реальных ситуациях.