Abstract
Сontent
Introduction
The purpose ofthis work is to develop a mathematical model of transient heat for the current three-zone reheating furnace light-section rolling shop while you are in the oven pieces of different sorts.
Pusher type reheating furnaces operate continuously only when full working space heating workpieces. In some plants for execution of orders on small lots small sections of rolled products is necessary to heat the metal of various sizes without stopping the oven. For these conditions the furnace is difficult in practice to determine the mode transition, i.e. frequency push blanks temperature in each zone workspace gas flow and other parameters. In this regard, there is a problem - to develop a mathematical model of transient heat that would provide heating billets to specified quality.
Pusher is a high-technology installations for the heating of billets for rolling. Structurally, the furnace consists of three zones - methodical, welding (upper and lower), and soaking. In the furnace the preform lie close to each other. In methodical and welding areas they move through the water-cooled skid pipes. In these areas, there is a bilateral asymmetrical heating of the metal, since on its intensity is higher than the bottom. In the soaking zone of metal lying on a monolithic hearth, heated from above (kept at a constant temperature of the surface of the workpiece).
Temperature is determined depending on the heating time and the geometrical dimensions.
τ=G/P,
where τ- heating time, s; G - the furnace vessel, kg; P - capacity in kg/s.
In methodical heating furnaces initial heating rate is limited by the size of the metal thermal stress, which is defined as the composition of the steel, and the thickness of the heated layer of the workpiece. At the end of the heating surface temperature and the temperature drop over the section of the workpiece must comply with the requirements of technology for the grade of steel.
Heat a large batch of blanks of the same size and the same grade of steel is not difficult when you follow a given technology. However, the finding in the working space of blanks of different thickness and chemical composition, requires the development of such a transient heat that would ensure the quality of the heating of two different batches of workpieces close to the technological requirements for these parties.
Pusher type reheating furnaces operate continuously only when full working space heating workpieces. In some plants for execution of orders on small lots small sections of rolled products is necessary to heat the metal of various sizes without stopping the oven. For these conditions the furnace is difficult in practice to determine the mode transition, i.e. frequency push blanks temperature in each zone workspace gas flow and other parameters. In this regard, there is a problem - to develop a mathematical model of transient heat that would provide heating billets to specified quality.
Formulation of the problem
In billet reheating furnace in a methodical and welding areas are on the skid tubes. Heating preforms made ??from two sides at their location in a continuous furnace. To calculate the temperature distribution over the thickness of the workpiece during the time you can take advantage of the differential equation of heat conduction for a one-dimensional temperature field:
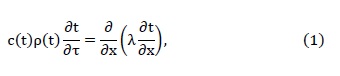
where λ(t), c(t), ρ(t) – respectively, the thermal conductivity, Вт/(мК); heat capacity, Дж/(кгК); density of the metal, кг/м3.
In the soaking zone of metal moving through the monolithic hearth is heated at a constant temperature of the surface tпк, equal to the final temperature of the metal surface.
To obtain a unique solution of the differential equation (1) is necessary to specify the conditions of uniqueness:
- the initial conditions:
at τ= 0 t = f(x) (2)
- boundary conditions:
at x=0, q=αвизл(tгв-tпв);
at x=lx, q=αнизл(tгн-tпн) (3)
where αвизл , αнизл - radiative heat transfer coefficients in the upper and lower zones of the furnace,Вт/(м2К);
tгв,tгн - the gas temperature in the upper and lower zones, °C;
tпв, tпн - surface temperature of the metal in the upper and lower zones, °C.
The coefficient of heat transfer by radiation with varying gas temperature along the length of the furnace (methodical zone) is calculated by the formula [4]:
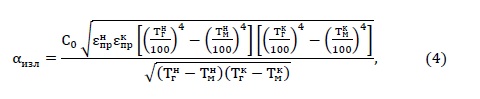
at a constant temperature along the length of the furnace (welding zone) by the formula:
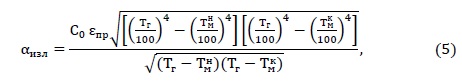
where С0 - ratio of blackbody radiation, Вт/(м2К4);
Tгн, Tгк - the gas temperature in the beginning and end of methodological zone К;
Tг - gas temperature along the length of the welding zone, К;
εпрн ,εпрк, εпр–given the degree of blackness of the beginning and end
methodological areas and along the length of the weld zone.
On the basis of the developed program were calculated heating of steel billets of various thickness in relation to three-zone reheating furnace rolling mill of "Donetskstal MZ" for the case of the simultaneous presence in the workspace blanks of various cross-sectional area. Assume that the furnace is heated preform thickness S1, and through which - while the blank fed into the furnace thinner S2. If the heating is carried out on the treatment of the workpiece S1, a workpiece thickness S2 will overheat, and when using the blank S2, a workpiece thickness S1, will nedogrevatsya.
To avoid the occurrence of thermal stress is assumed that the temperature of the onset of plastic deformation of the metal tпл=550°C, the surface temperature at the end of the welding zone tпк=1250°C. Articles zone - the zone of gradual heating of the metal, so in the end zone methodical metal must be malleable.
The results of simulation of heating wood thickness S1=0,21 м и S2=0,18 м are shown in Figure 1.
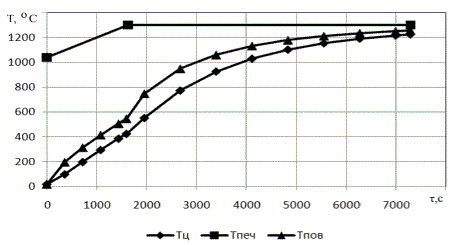
Changing the mode of heating the metal can occur in the case of heating the metal pieces the same thickness, but different brands. To this end, consider the heating wood thickness S = 0.21 m for different values ??of the thermal conductivity λ1=20 Вт/(мК) и λ2=40 Вт/(мК). The table shows the results of the simulation of such preparations.
Table. The simulation results billet heating for various values of the thermal conductivity.
| The coefficient of thermal conductivity of the material blanks,λ Вт/(мК) | The oven temperature,°C | Temperature of the preform,°C | |||||
| Methodological zone | The welding zone | End of methodological areas | The end of the welding zone | ||||
| Start | End | End | Surfaces | Mid | Surfaces | Mid | |
| 20 | 809 | 1305 | 1305 | 555 | 316 | 1246 | 1185 |
| 40 | 1060 | 1295 | 1295 | 545 | 410 | 1249 | 1226 |
The gas temperature at the beginning of the methodological area for workpieces with a thermal conductivity λ=20 Вт/(мК) less than for the blanks with a coefficient of thermal conductivity λ=40 Вт/(мК).
With less coefficient of thermal conductivity of the heat to the inside of the body is given less than more. In this regard, at a lower coefficient of thermal conductivity of the surface temperature is increasing rapidly. This leads to the fact that the surface temperature corresponding to the temperature of the onset of plastic deformation is achieved at lower gas temperature than at a higher coefficient of thermal conductivity. The temperature difference across the section blank at a lower thermal conductivity will be great. At the end of the methodological zone temperature gradient over the cross section of the body with a coefficient of thermal conductivity λ=20 Вт/(мК) equals Δt1=239°C,and when λ=40 Вт/(мК) Δt2=135°C. At such temperature changes on the thickness of the preform to the temperature at which plastic deformation determined by the weight-average temperatures across the section. At the end of the heating produced the desired quality of heating: the temperature of the surface satisfies the set and the temperature difference Δt1=61°C and Δt2=23°C.
Conclusion
Thus, as a result of the research and developed the algorithm is simulated heating the metal at a constant production rate and varying the thickness of the workpiece. Changing the thickness of the workpiece changes the heating time in accordance with the results achieved may change the residence time of the metal in the furnace zones. This in turn leads to a change in the speed of advance of the metal in the furnace. Change in temperature leads to a change in the economic performance of the furnace. In the future we plan to carry out research on the actual reheating furnace, not only on a constant, but at a variable.
In writing this essay master's work is not yet completed. Final completion in January 2014.
References
- Ткаченко В.Н. Математическое моделирование, идентификация и управление технологическими процессами тепловой обработки материалов / В.Н. Ткаченко. – К.: Наукова думка, 2008.- 243с.
- Металлургическая теплотехника/ Под научной редакцией Н.А. Кривандина.- М.: Металлургия, 1986. - 243с.
- Гинкул С.И. Применение ЭВМ для расчета нагрева металла в методической печи/ Е.И. Казанцев, С.И. Гинкул, В.В. Антонов, Н.В. Гончаров// Сталь. – 1973.- №1 – с.77-79.
- Гинкул С.И. Исследование температурного режима нагревательных печей прокатных станов при изменении сортамента нагреваемого металла/ С.И. Гинкул, А.Н. Лебедев, Ю.В. Подобед, Ю.М. Сапронова// Научные труды Донецкого национального технического университета. Серия «Металлургия». Вып. 12(177) – Донецк, ООО «Цифровая типография», 2010 – с.201 – 206.
- Теоретические основы теплотехники. Теплотехнический эксперимент. Справочник/ Под общей редакцией В.А. Григорьева и В.М. Зорина. Книга 2.-М.:Энергоатомиздат, 1988.-557с.
- Мастрюков Б.С. Теория, конструкции и расчеты металлургических печей/ Б.С. Мастрюков. – М.: Металлургия, 1986, - т.2. – 376с.
- Казанцев Е.И. Промышленные печи. - М.: Металлургия, 1975. - 368с.
- Теплообмен и тепловые режимы в промышленных печах/ Ю.И. Розегард, Б.Б. Потапов, В.М. Ольшанский, А.В. Бородулин// К.: Донецк: Вища школа 1986. – 296с.
- Казанцев Е.И. Выбор оптимального температурного режима по минимуму окалинообразования/ Е.И. Казанцев, Г.П. Вынов, С.И. Гинкул// Изв. вузов Черная металлургия – 1977. - №9. – с.165-168.
