ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

При работе крана происходит постоянное чередование направления движения крана, тележки и крюка. Так, работа механизма подъема состоит из процессов подъема и опускания груза и процессов подъема и опускания пустого крюка. Для увеличения производительности крана используют принцип совмещения операций. Время пауз, в течение которых двигатель не включен и механизм не работает, используется для навешивания груза на крюк и освобождения крюка и для подготовки к следующему процессу работы механизма. Каждый процесс движения, в свою очередь, может быть разделен на периоды неустановившегося движения (в течение которых происходит разгон или замедление движущихся масс груза и механизма) и период движения с установившейся скоростью.

Для кранов общего назначения с машинным приводом установлены режимы работы: легкий, средний и тяжелый. Для каждого механизма режим работы определяется отдельно, режим работы крана в целом устанавливается по механизму главного подъема.

Обычно кран имеет две тележки: тележку передвижения и грузовую тележку. Грузовая тележка присутствует в единственном числе, но в некоторых случаях их число может быть доведено до двух.

К приводу тележек предъявляются довольно жесткие требования: он должен обеспечивать быстрый и в то же время плавный разгон, постоянство ускорения независимо от скорости переключения контактов командоконтроллера, возможность реверса, высокую надежность и стабильность работы в условиях как высоких, так и низких температур, а также при высокой влажности, запыленности окружающей среды и присутствии агрессивных газов и дыма.

Использование оптимальных режимов работы грузовой тележки позволяет: уменьшить динамические нагрузки на механизм перемещения тележки, обеспечивая отсутствие ударов; избежать колебаний груза закрепленного на гибком подвесе [1].

1. Обзор научных статей

Качество многих технологических процессов зависит от перемещения грузов подъемно-транспортными машинами. Вопросы оптимизации режимов движения крановых механизмов рассматриваются в работах таких ученых как В.П. Балашов, Н.А. Лобов, Б.В. Квартальнов, В.И. Ключев, Ю.А. Борцов, Б.Ш. Бургин, В.Н. Тищенко, Г.Г. Соколовский, Л.Б. Масандилов, Р.П. Герасимяк, И.Я. Браславский и др.

В работе Дорофеева А. А. [2] составлена трехмассовая математическая модель движения мостового крана по рельсовому пути, отличающаяся от известных учетом упругого скольжения вращающихся колес относительно рельсов, а также учетом поперечного смещения и поворота в горизонтальной плоскости мостового крана в пределах зазоров между ребордами колес и рельсами подкранового пути.

В настоящее время для подавляющего большинства грузоподъемных кранов мостового типа в качестве электропривода рациональным является использование асинхронного электропривода (АЭП), как наиболее простого, дешевого и надежного. В работе Однокопылова И. Г. [3] разработана математическая модель для исследования в различных режимах работы АЭП механизма подъема крана мостового типа, отличающаяся тем, что в ней учитывается упругий характер механической части крана, влияние электромагнитного тормоза, насыщение асинхронного двигателя, наличие преобразовательного устройства. Выявлены и обоснованы информативные параметры АД, характеризующие массу груза на крюке механизма подъема крана для ограничения его грузоподъемности.

В работе Ловейкина В. С. составлена двухмассовая динамическая расчетная схема «тележка - груз». Проанализированы результаты оптимизации переходных режимов движения тележки с грузом через интегральные критерии. Проведена оптимизация режимов движения крановой тележки с грузом с помощью комплексного критерия. Опубликованы структура и общий алгоритм работы системы для реализации оптимального управления крановой тележкой на практике [4].

Не смотря на достаточно широкое исследование вопроса колебаний груза некоторые способы, которые позволяют избежать колебаний, связаны с динамическими нагрузками на механизм перемещения тележки, что является нежелательным. Некоторые способы невозможно применять на практике. Кроме того, не все способы обеспечивают полное устранение колебаний в конце пути тележки или не устраняют их во время движения. Большинство известных способов устранения колебаний груза не обеспечивают желанных режимов движения, что не позволяет в полной мере использовать возможности пролетного крана.

В связи с этим возникает необходимость определения оптимальных законов движения крановой тележки, при котором колебания исчезали на протяжении переходных режимов ее движения и которые не приводили к значительным нагрузкам на конструкцию. Важным вопросом является обоснование структуры та алгоритмов работы системы, которая могла бы реализовать оптимальное управление движением крановой тележки [2].

2. Актуальность темы

Раскачивание груза являются причиной неравномерного движения крановой тележки, дополнительных нагрузок на элементы грузоподъемной машины. Они создают неудобства, которые угрожают безопасности рабочих, уменьшают продуктивность погрузочно-разгрузочных, транспортных операций. Колебания груза усложняют прицельное наведение грузозахватываюшего устройства и установки груза на заданное место. Особенно это относиться к грузам с большими габаритами [5].

Обзор литературы показал, что в исследованиях работы крановых механизмов достаточно детально рассмотрено динамику их движения на протяжении переходных режимов. Значительное внимание уделена проблеме устранения колебаний груза. Однако большинство предлагаемых методов решения этой проблемы не удовлетворяют требованиям современных технологических процессов транспортировки груза. Таким образом, работа крановой тележки обязана обеспечивать высокую эксплуатационную эффективность крана, при этом нагрузки на крановую тележку должны быть минимальными [6].

Принимая во внимание все это, проблема устранения колебаний груза подвешенного на гибком канате является достаточно актуальной.

3. Цель и задачи исследования

Целью работы является устранение колебаний груза за счет формирования оптимальных переходных режимов движения крановой тележки и разработка системы, которая обеспечит желательное управляющее воздействие на механизм перемещения.

Для достижения поставленной цели необходимо решить следующие задачи:

  1. выполнить анализ существующих исследований в направлении устранения колебаний груза, закрепленного на гибком подвесе;
  2. определить законы управления движением механизма подъема, при которых колебания устраняются;
  3. разработать методику проведения экспериментов и исследовать основные характеристики движения модели тележки с подвешенным на нее грузом;
  4. на основе проведенных исследований предложить функциональную схему управления движением механизма подъема;
  5. показать положительные стороны от использования системы управления приводным механизмом.

4. Математическая модель движения тележки с грузом

Для исследования движения грузоподъемного механизма была составлена трехмассовая динамическая схема (рис. 1).

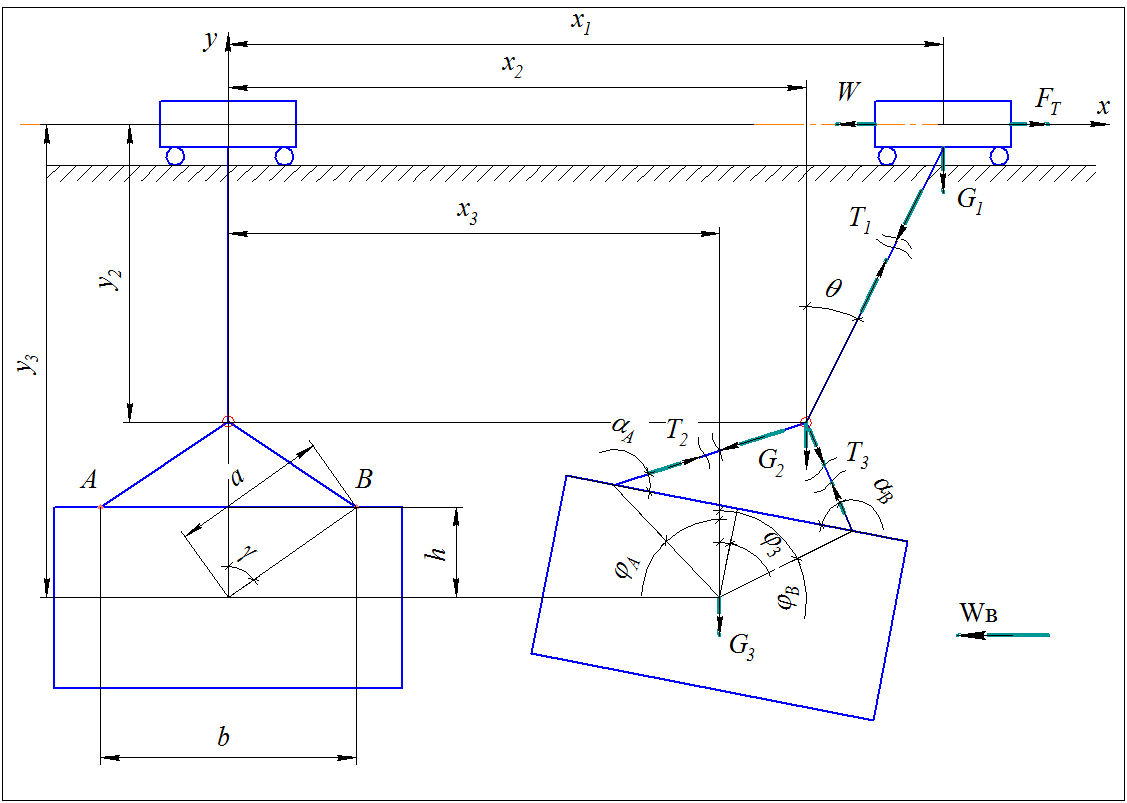
Расчетная динамичная схема движения грузоподъемного механизма

Рисунок 1 - Расчетная динамичная схема движения грузоподъемного механизма

На рисунке 1: m1 – масса грузоподъемной тележки; FТ – суммарное тяговое усилие; W – сила сопротивления движению тележки; T1 – сила натяжения каната; T2, T3 –силы натяжения строп; G1 – сила тяжести грузоподъемной тележки; G2 – сила тяжести крюка; G3 – сила тяжести груза; φ3 – угол поворота груза; αА, αВ – угол между грузом и стропой; θ – угол отклонения каната от начального положения; h – расстояние по вертикали между центром тяжести груза и местом закрепления строп; b – расстояния межу местами закрепления строп; a – расстояние между центром тяжести груза и местом закрепления строп.

Используя уравнения движения твердого тела [7], составлена система дифференциальных уравнений:

Cистема дифференциальных уравнений

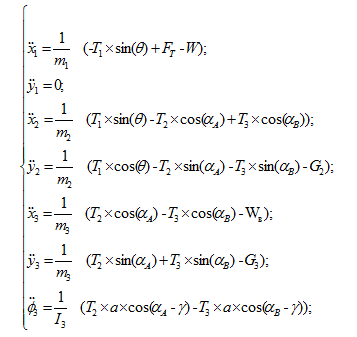
где Cила натяжения каната - сила натяжения каната;

Коэффициент жесткости каната - коэффициент жесткости каната;

Е - модуль упругости материала каната;

Площадь сечения каната - площадь сечения каната;

d1 - диаметр каната;

c - коэффициент заполнения сечения каната;

Удлинение каната - удлинение каната;

Длина каната во время движения - длина каната во время движения;

l10 - длина каната в положении равновесия;

Скорость удлинения каната - скорость удлинения каната;

β - коэффициент рассеивания энергии;

Сила натяжения строп - сила натяжения строп;

Коэффициент жесткости строп - коэффициент жесткости строп;

Площадь сечения строп - площадь сечения строп;

Е - модуль упругости материала строп;

d2, d3 - диаметр строп;

с - коэффициент заполнения сечения строп;

Удлинение строп - удлинение строп;

Длина строп во время движения - длина строп во время движения;

l20, l30 - длина строп в положении равновесия;

Cкорость удлинения строп - скорость удлинения строп;

Cила тяжести тележки - сила тяжести тележки;

m1 - масса тележки;

g - ускорение свободного падения;

Cила тяжести крюка - сила тяжести крюка;

m2 - масса крюка;

Cила тяжести груза - сила тяжести груза;

m3 - масса груза;

Угол отклонения каната от начального положения - угол отклонения каната от начального положения;

Угол между грузом и стропой - угол между грузом и стропой;

Угол между грузом и стропой - угол между грузом и стропой;

Расстояние между центром тяжести груза и местом закрепления строп - расстояние между центром тяжести груза и местом закрепления строп;

h - расстояние по вертикали между центром тяжести груза и местом закрепления строп;

b - расстояния межу местами закрепления строп;

Cила сопротивления ветра при движении - сила сопротивления воздуха при движении груза;

ρ - плотность воздуха;

са - коэффициент аэродинамической силы;

n - коэффициент перегрузки.

5. Законы управления механизмом передвижения тележки

Для проведения оптимизации переходных режимов движения грузовой тележки были использованы законы управления механизмом перемещения тележки (трапецеидальная тахограмма перемещения тележки с постоянным ускорением, трапецеидальная тахограмма перемещения тележки с плавно переменным ускорением и др.).

Все использованные законы полностью или частично устраняют колебания груза и динамическую нагрузку механизма привода тележки и металлоконструкций крана, что обеспечивает плавность движения механизмов перемещения.

Наиболее эффективным законом управления скоростью движения тележки на переходных участках движения является трапецеидальная тахограмма перемещения тележки с оптимизированным участком остановки. Для этого закона уравнения движения тележки на участке остановки задается интерполяционным полиномом с узлами, равномерно расположенными на отрезке tо. Принято 6 узлов (рис. 2), положение первого и шестого заданные (Vдл и 0), а значение скорости в 2-5 узлах являются параметрами, требующими оптимизации.

Исходное положение узлов интерполяции

Рисунок 2 - Исходное положение узлов интерполяции

Скорость движения тележки определяется по формулам:

Скорость движения тележки

где V1 ... V6 - значения скоростей соответствующих узлов интерполяции, м /с;

t1…t6 - значение времени соответствующих узлов интерполяции, с.

Условием существенного снижения раскачивания груза после остановки тележки является оптимизация значений относительных скоростей (узлов интерполяции) (V1/V ... V6/V) на участке остановки. Подбор значений относительных скоростей требует учета таких величин как масса груза m3, длина каната l10 и время остановки tо. Для трапецеидальной тахограммы движения тележки с оптимизированной участком остановки при tо = 3,85 с, m3 = 5000 кг, l10 = 6 м (рис. 3) методом покоординатного спуска получены рациональные узловые значения относительных скоростей V1/V = 1, V2/V = 0,58, V3/V = 0,48, V4/V = 0,28, V5/V = 0,38, V6/V = 0, при этом максимальное отклонение груза от вертикали после остановки движения тележки составляет 0,008 м, что значительно меньше, чем для других тахограмм.

Трапецеидальная тахограмма перемещения тележки с оптимизированной участком остановки

Рисунок 3 - Трапецеидальная тахограмма перемещения тележки с оптимизированным участком остановки

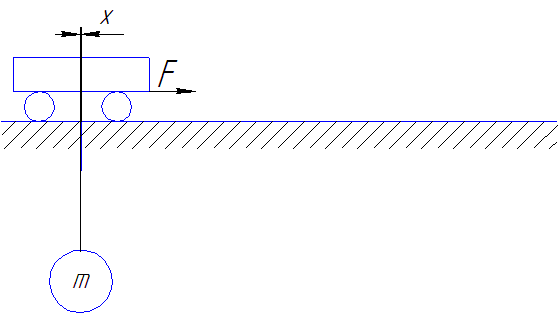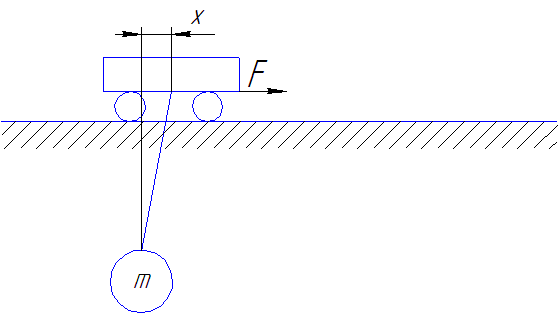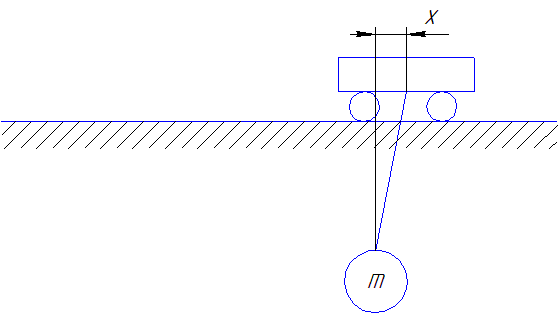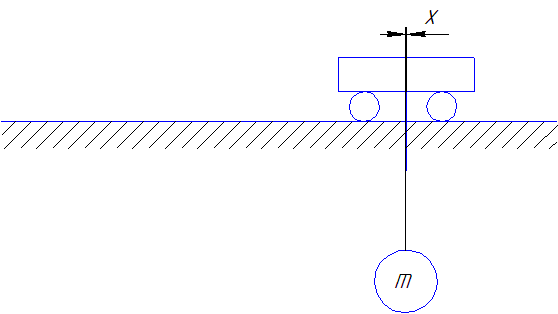
Схема движение тележки с грузом при применении закона управления <q>Трапецеидальная тахограмма перемещения тележки с оптимизированной участком остановки</q>

Рисунок 4 - Схема движения тележки с грузом при применении закона управления Трапецеидальная тахограмма перемещения тележки с оптимизированной участком остановки (сделано в mp_gif_animator, 8 кадров, 6 повторений, задержка между кадрами 0,45 с.)

Выводы

  1. В работе разработана и реализована в системе Mathcad математическая модель движения тележки с грузом;
  2. Получены законы движения тележки, которые полностью или частично устраняют колебания груза, что обеспечивает плавность движения механизмов перемещения;
  3. Разработана математическая модель рационального закона управления скоростью движения тележки мостового крана на участке остановки, практически исключающего остаточное колебание груза. Для tо = 3,85 с, m3= 5000 кг, l1= 6 м, Vдл=0,8 м/с максимальное отклонение груза от вертикали после остановки тележки составляет 0,008 м, что значительно меньше, чем для других тахограмм при аналогичных параметрах.

В дальнейшем планируется разработать алгоритм и систему управления движения тележки, обеспечивающих минимальное раскачивание груза.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Абрамович И.И., Березин В.Н., Яуреи А.Г. Грузоподъемные краны промышленных предприятий. – М.: Машиностроение, 1989. – 360 с.
  2. Дорофеев А. А. Разработка и исследование систем электроприводов, обеспечивающих бесперекосное движение мостовых кранов : Диссертация ... кандидата технических наук. – Липецк, 2010. – 231 с.
  3. Однокопылов И. Г. Асинхронный электропривод механизма подъема крана мостового типа с повышенной безопасностью и живучестью : Диссертация ... кандидата технических наук. – Томск, 2008. – 162 c.
  4. Ловейкин В. С. Оптимизация переходных режимов движения механизма передвижения тележки грузоподъемных машин/ Ловейкин В. С. , Ярошенко В.Ф. // Весник Харьковского национального технического университета сельского хазяйства шимени Петра Василенка. – 2007 – 460 с.
  5. Бортяков Д.Е., Орлов А.Н. Специальные грузоподъемные машины.СПб.: Изд-во Политехн. ун-та, 2005. 64 с
  6. Александров Н.П., Колобов Л.Н., Лобов Н.А. и др. Грузоподъемные машины. М.: Машиностроение, 1986г. -400с.
  7. Яблонский А. А. Курс теоретической механики. Часть II. Динамика. – Москва «Высшая школа», 1984. – 411 с.
  8. Очков В.Ф. Mathcad 14 для студентов и инженеров. С.-Пб.: БХВ-Петербург, 2007.
  9. ГОСТ 1451-77 Краны грузоподъёмные. Нагрузка ветровая. Нормы и метод определения.
  10. Крановое электрооборудование: Справочник / Ю.В. Алексеев, А.П. Богословский. - М.: Энергия, 1979г.