Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Огляд наукових статей
- 2. Актуальність теми
- 3. Мета і завдання роботи
- 4. Математична модель руху візка з вантажем
- 5. Закони управління механізмом переміщення візка
- Висновки
- Перелік посилань
Вступ
При роботі крана відбувається постійне чергування напрямку руху крана, візка і гака. Так, робота механізму підйому складається з процесів підйому та опускання вантажу і процесів підйому та опускання порожнього гака. Для збільшення продуктивності крана використовують принцип суміщення операцій. Час пауз, протягом яких двигун не включений і механізм не працює, використовується для навішування вантажу на гак і звільнення гака і для підготовки до наступного процесу роботи механізму. Кожен процес руху, у свою чергу, може бути розділений на періоди несталого руху (протягом яких відбувається розгін або уповільнення рухомих мас вантажу і механізму) і період руху з усталеною швидкістю.
Для кранів загального призначення з машинним приводом встановлені режими роботи: легкий, середній і важкий. Для кожного механізму режим роботи визначається окремо, режим роботи крана в цілому встановлюється за механізмом головного підйому.
До приводу візків пред'являються досить жорсткі вимоги: він повинен забезпечувати швидкий і в той - же час плавний розгін, сталість прискорення незалежно від швидкості перемикання контактів командоконтролера, можливість реверсу, високу надійність і стабільність роботи в умовах як високих, так і низьких температур, а також при високій вологості, запиленості навколишнього середовища та присутності агресивних газів і диму.
Використання оптимальних режимів роботи вантажного візка дозволяє: зменшити динамічні навантаження на механізм переміщення візка, забезпечуючи відсутність ударів; уникнути коливань вантажу закріпленого на гнучкому підвісі [1].
1. Огляд наукових статей
Якість багатьох технологічних процесів залежить від переміщення вантажів підйомно-транспортними машинами. Питання оптимізації режимів руху кранових механізмів розглядаються в роботах таких вчених як В.П. Балашов, Н.А. Лобов, Б.В. Квартальнов, В.І. Ключів, Ю.А. Борців, Б.Ш. Бургін, В.Н. Тищенко, Г.Г. Соколовський, Л.Б. Масанділов, Р.П. Герасімяк, І.Я. Браславський та ін.
У роботі Дорофєєва О. А. [2] складена трьохмасова математична модель руху мостового крана по рейковому шляху, що відрізняється від відомих урахуванням пружного ковзання обертових коліс відносно рейок, а також урахуванням поперечного зсуву і повороту в горизонтальній площині мостового крана в межах зазорів між ребордами коліс і рейками підкранової колії.
В даний час для переважної більшості вантажопідйомних кранів мостового типу в якості електроприводу раціональним є використання асинхронного електроприводу (АЕП), як найбільш простого, дешевого і надійного. У роботі Однокопилова І. Г. [3] розроблена математична модель для дослідження в різних режимах роботи АЕП механізму підйому крана мостового типу, що відрізняється тим, що в ній враховується пружний характер механічної частини крана, вплив електромагнітного гальма, насичення асинхронного двигуна, наявність перетворювального пристрою . Виявлено та обґрунтовано інформативні параметри АД, що характеризують масу вантажу на гаку механізму підйому крана для обмеження його вантажопідйомності.
У роботі Ловейкіна В. С. складена двохмасова динамічна розрахункова схема «візок - вантаж». Проведена оптимізація режимів руху кранового візка з вантажем за допомогою комплексного критерію. Розроблено структуру та загальний алгоритм роботи системи для реалізації оптимального управління крановим візком на практиці [4].
Не дивлячись на досить широке дослідження питання коливань вантажу деякі способи, які дозволяють уникнути коливань, пов'язані з динамічними навантаженнями на механізм переміщення візка, що є не бажаним. Деякі способи неможливо застосовувати на практиці. Крім того, не всі способи забезпечують повне усунення коливань в кінці шляху візка або не усувають їх під час руху. Більшість відомих способів усунення коливань вантажу не забезпечують бажаних режимів руху, що не дозволяє в повній мірі використовувати можливості пролітного крана.
У зв'язку з цим виникає необхідність визначення оптимальних законів руху крановим візка, при якому коливання зникали протягом перехідних режимів її руху і які не призводили до значних навантажень на конструкцію. Важливим питанням є обґрунтування структури та алгоритмів роботи системи, яка могла б реалізувати оптимальне управління рухом крановим візка [2].
2. Актуальність теми
Розгойдування вантажу, що виникають на протяг режимів руху крановим візка, є причиною його нерівномірного руху, додаткових навантажень на елементи вантажопідйомної машини. Вони створюють незручності, які загрожують безпеці робітників, зменшують продуктивність навантажувально-розвантажувальних, транспортних операцій. Коливання вантажу ускладнюють прицільне наведення вантажозахоплюючого пристрою та установки вантажу на задане місце. Особливо це стосується до вантажів з великими габаритами [5].
Огляд літератури показав, що в існуючих теоретичних та експериментальних дослідженнях роботи кранових механізмів досить детально розглянуто динаміку їх руху протягом перехідних режимів, значна увага приділена проблемі усунення коливань вантажу, однак більшість запропонованих методів вирішення цієї проблеми не задовольняють вимогам сучасних технологічних процесів транспортування вантажу, а якщо задовольняють, то при цьому робота крана супроводжується великими динамічними навантаженнями. Таким чином, робота кранового візка зобов'язана забезпечувати високу експлуатаційну ефективність крана, при цьому навантаження на крановий візок повинні бути мінімальними [6].
Беручи до уваги велику кількість працюючих в наш час кранів та збільшення вимог щодо створення безпечних умов роботи з ними і збільшення їх продуктивності, проблема усунення коливань вантажу, підвішеного на гнучкому канаті, є досить актуальною.
3. Мета і завдання роботи
Метою роботи є усунення коливань вантажу за рахунок формування оптимальних перехідних режимів руху механізму пересування кранового візка.
Для досягнення поставленої мети необхідно вирішити наступні завдання:
- виконати аналіз існуючих досліджень в напрямку усунення коливань вантажу, закріпленого на гнучкому підвісі;
- розглянути можливі закони управління рухом механізму підйому, при яких коливання усуваються;
- розробити та реалізувати програмно математичну модель перехідних процесів руху візка з підвішеним вантажем, визначити її параметри;
- розробити методику проведення обчислювальних експериментів з встановлення закономірностей впливу закону управління рухом візка на коливання підвішеного вантажу, визначити раціональний закон.
4. Математична модель руху візка з вантажем
Для дослідження руху вантажопідйомного механізму була складена трьохмасова динамічна схема (рис. 1).
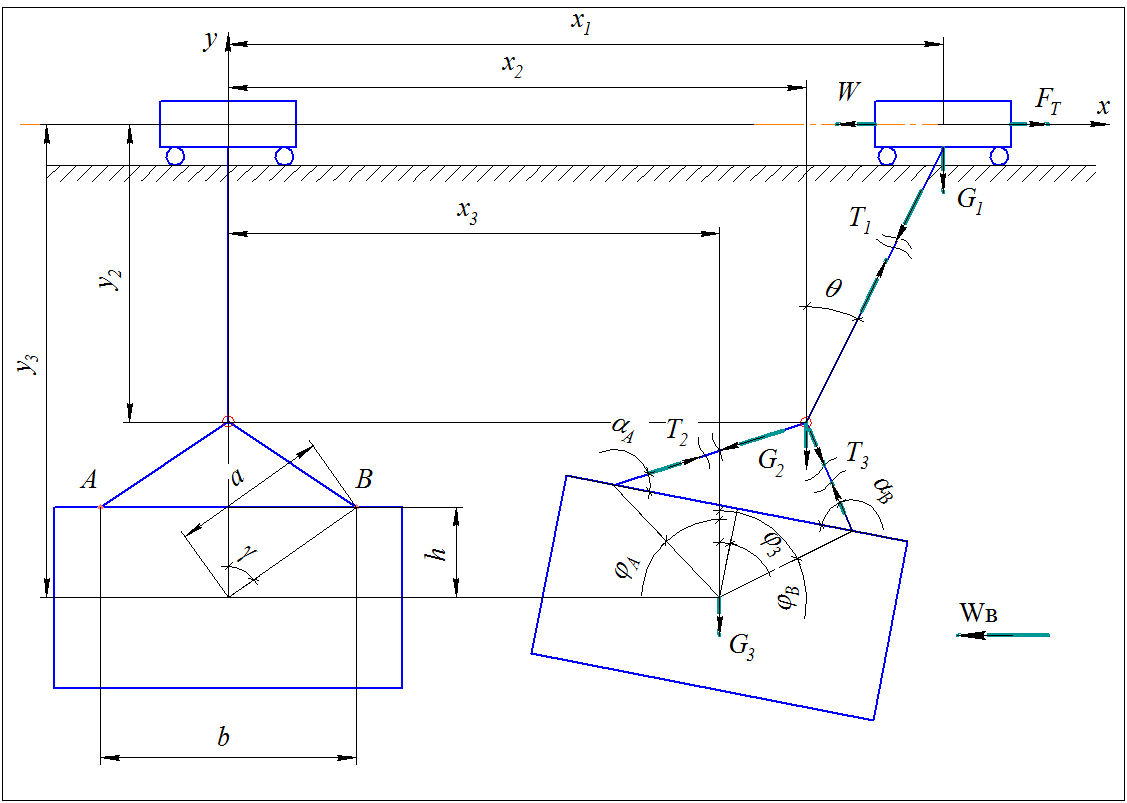
Рисунок 1 - Розрахункова динамічна схема руху вантажопідйомного механізму
На рисунку 1: m1 - маса вантажопідйомної візки; FТ - сумарне тягове зусилля; W - сила опору руху візка; T1 - сила натягу каната; T2, T3-сили натягу строп; G1 - сила тяжіння вантажопідйомної візки; G2 - сила тяжіння гака; G3 - сила тяжіння вантажу; φ3 - кут повороту вантажу; αА, αB - кут між вантажем і стропою; θ - кут відхилення каната від початкового положення; h - відстань по вертикалі між центром ваги вантажу і місцем закріплення строп; b - відстані межу місцями закріплення строп; a - відстань між центром ваги вантажу і місцем закріплення строп.
Використовуючи рівняння руху твердого тіла [7], складена система диференційних рівнянь:
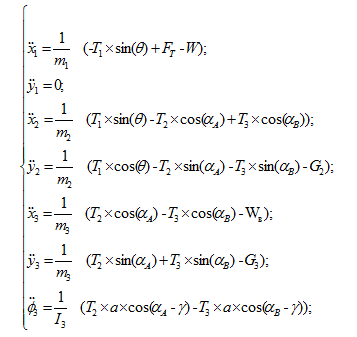
де  - сила натягу канату;
- сила натягу канату;
 - коефіцієнт жорсткості канату;
- коефіцієнт жорсткості канату;
Е - модуль пружності матеріалу канату;
 - площа перерізу канату;
- площа перерізу канату;
d1 - діаметр канату;
c - коефіцієнт заповнення перетину канату;
 - подовження канату;
- подовження канату;
 - довжина канату під час руху;
- довжина канату під час руху;
l10 - довжина канату в положенні рівноваги;
 - швидкість подовження канату;
- швидкість подовження канату;
β - коефіцієнт розсіювання енергії;
 - сила натягу стропів;
- сила натягу стропів;
 - коефіцієнт жорсткості стропів;
- коефіцієнт жорсткості стропів;
 - площа перерізу стропів;
- площа перерізу стропів;
Е - модуль пружності матеріалу стропів;
d2, d3 - діаметр стропів;
с - коефіцієнт заповнення перетину стропів;
 - подовження стропів;
- подовження стропів;
 - довжина стропів під час руху;
- довжина стропів під час руху;
l20, l30 - довжина стропів в положенні рівноваги;
 - швидкість подовження стропів;
- швидкість подовження стропів;
 - сили тяжіння візку;
- сили тяжіння візку;
m1 - маса візку;
g - прискорення вільного падіння;
 - сили тяжіння причіпного пристрою;
- сили тяжіння причіпного пристрою;
m2 - маса причіпного пристрою;
 - сили тяжіння вантажу;
- сили тяжіння вантажу;
m3 - маса вантажу;
 - кут відхилення канату від початкового положення;
- кут відхилення канату від початкового положення;
 - кут між вантажем і стропою;
- кут між вантажем і стропою;
 - кут між вантажем і стропою;
- кут між вантажем і стропою;
 - відстань між центром ваги вантажу і місцем закріплення стропів;
- відстань між центром ваги вантажу і місцем закріплення стропів;
h - відстань по вертикалі між центром ваги вантажу і місцем закріплення стропів;
b - відстані між місцями закріплення строп;
 - сила опору вітру при русі;
- сила опору вітру при русі;
ρ - щільність повітря;
са - коефіцієнт аеродинамічної сили;
n - коефіцієнт перевантаження.
5. Закони управління механізмом переміщення візка
Для проведення оптимізації перехідних режимів руху вантажного візка були використані закони управління механізмом переміщення візка (трапециідальна тахограма переміщення візка з постійним прискоренням, трапецеїдальна тахограма переміщення візка з плавно змінним прискоренням та ін.).
Всі використані закони повністю або частково усувають коливання вантажу і динамічне навантаження механізму приводу візки і металоконструкцій крана, що забезпечує плавність руху механізмів переміщення.
Найбільш ефективним законом керування швидкістю руху візка на перехідних ділянках руху є трапециідальна тахограма переміщення візка з оптимізованою ділянкою зупинки. Для цього закону рівняння руху візка на ділянці зупинки задається інтерполяційним поліномом з вузлами, рівномірно розташованими на відрізку t з. Прийнято 6 вузлів (рис. 2), положення першого та шостого задані (Vтр і 0), а значення швидкості в 2-5 вузлах є параметрами, що вимагають оптимізації.
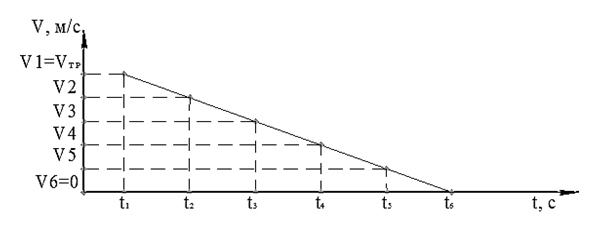
Рисунок 2 - Початкове положення вузлів інтерполяції
Швидкість руху візка визначається за формулами:
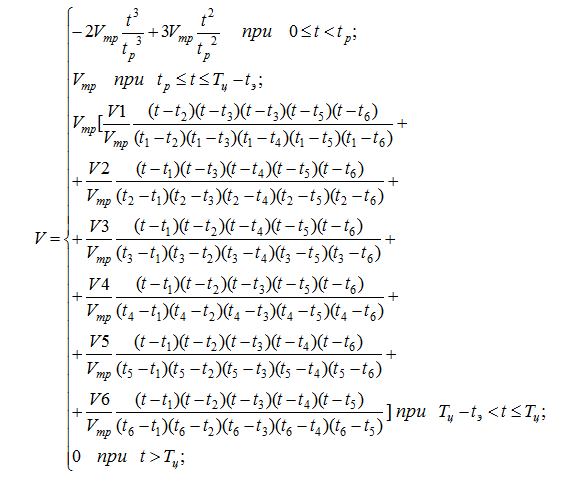
де V1 ... V6 - значення швидкостей відповідних вузлів інтерполяції, м/с;
t 1 ... t 6 - значення часу відповідних вузлів інтерполяції, с.
Умовою істотного зниження розгойдування вантажу після зупинки візка є оптимізація значень відносних швидкостей (вузлів інтерполяції) (V1/V ... V6/V) на ділянці зупинки. Підбір значень відносних швидкостей вимагає врахування таких величин як маса вантажу m3, довжина канату l10 і час зупинки tз. Для трапецеїдальної тахограми руху візка з оптимізованою ділянкою зупинки при tз = 3,85 с, m3 = 5000 кг, l10 = 6 м (рис. 3) методом покоординатного спуску отримані раціональні вузлові значення відносних швидкостей V1/V = 1, V2/V = 0,58, V3/V = 0,48, V4/V = 0,28, V5/V = 0,38, V6/V = 0, при цьому максимальне відхилення вантажу від вертикалі після зупинки руху візка становить 0,008 м, що значно менше, ніж для інших тахограм.
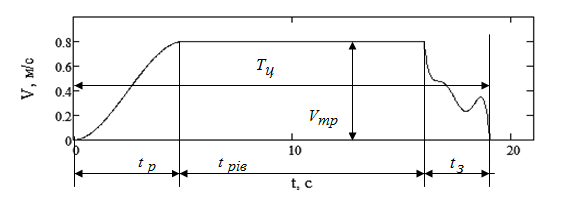
Рисунок 3 - Трапециідальна тахограма переміщення візка з оптимізованою ділянкою зупинки
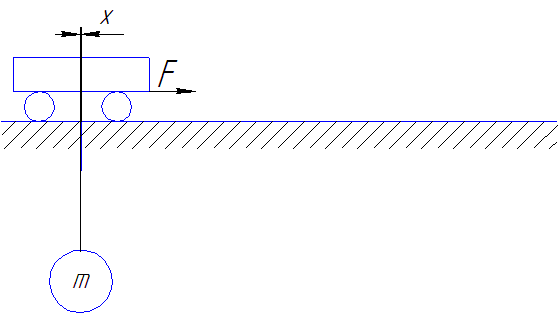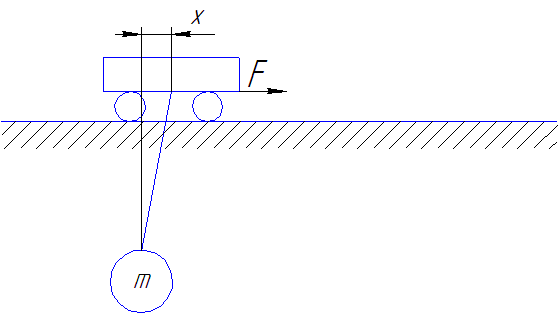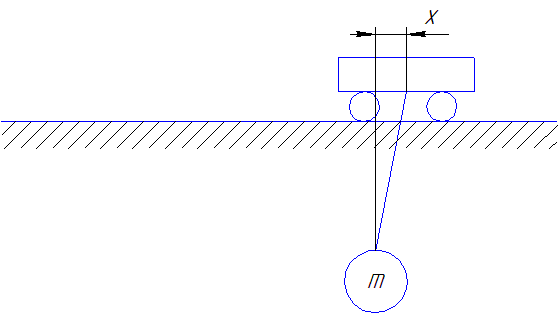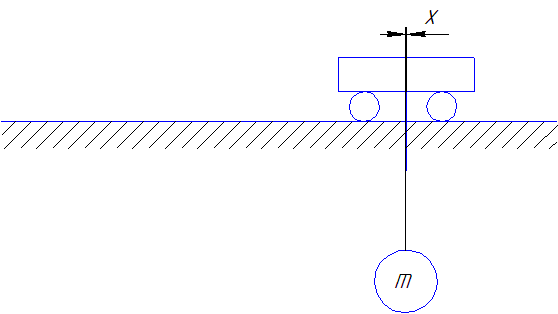
Рисунок 4 - Схема руху візка з вантажем при застосуванні закону управління Трапециідальна тахограмма переміщення візка з оптимізованою ділянкою зупинки
(зроблено в mp_gif_animator, 8 кадрів, 6 повторень, затримка між кадрами 0,45 с)
Висновки
- У роботі розроблена і реалізована в системі Mathcad математична модель руху візка з вантажем.
- Отримано закони руху візка, які повністю або частково усувають коливання вантажу, що забезпечує плавність руху механізмів переміщення;
- Розроблено математичну модель раціонального закону керування швидкістю руху візка мостового крана на ділянці зупинки, практично виключає залишкове коливання вантажу. Для tз = 3,85 с, m3 = 5000 кг, l1 = 6 м, Vтр = 0,8 м/с максимальне відхилення вантажу від вертикалі після зупинки візка становить 0,008 м, що значно менше, ніж для інших тахограм за аналогічних параметрах.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.
Перелік посилань
- Абрамович И.И., Березин В.Н., Яуреи А.Г. Грузоподъемные краны промышленных предприятий. – М.: Машиностроение, 1989. – 360 с.
- Дорофеев А. А. Разработка и исследование систем электроприводов, обеспечивающих бесперекосное движение мостовых кранов : Диссертация ... кандидата технических наук. – Липецк, 2010. – 231 с.
- Однокопылов И. Г. Асинхронный электропривод механизма подъема крана мостового типа с повышенной безопасностью и живучестью : Диссертация ... кандидата технических наук. – Томск, 2008. – 162 c.
- Ловейкин В. С. Оптимизация переходных режимов движения механизма передвижения тележки грузоподъемных машин/ Ловейкин В. С. , Ярошенко В.Ф. // Весник Харьковского национального технического университета сельского хазяйства шимени Петра Василенка. – 2007 – 460 с.
- Бортяков Д.Е., Орлов А.Н. Специальные грузоподъемные машины.СПб.: Изд-во Политехн. ун-та, 2005. 64 с
- Александров Н.П., Колобов Л.Н., Лобов Н.А. и др. Грузоподъемные машины. М.: Машиностроение, 1986г. -400с.
- Яблонский А. А. Курс теоретической механики. Часть II. Динамика. – Москва «Высшая школа», 1984. – 411 с.
- Очков В.Ф. Mathcad 14 для студентов и инженеров. С.-Пб.: БХВ-Петербург, 2007.
- ГОСТ 1451-77 Краны грузоподъёмные. Нагрузка ветровая. Нормы и метод определения.
- Крановое электрооборудование: Справочник / Ю.В. Алексеев, А.П. Богословский. - М.: Энергия, 1979г.
