Аннотация
Ansari A.A., Deshpande D.M. Исследование автоколебаний при моделировании гармонического осциллятора с использованием комплексов моделирования. Это статья демонстрирует моделирование установившийся режим работы асинхронного двигателя с помощью программы MATLAB смоделирован трехфазный асинхронный двигатель с использованием SIMULINK.
1. Ввведение
В последние годы контроль асинхронного двигателя, используемого широко в промышленности, получил большие распространенные исследовательские интересы. Индукционные моделированные машины привлекли внимание исследователей не только потому, что такие машины производятся и используются в наибольшем количестве, но и в связи с их разнообразными режимами работы как в стационарных и динамических состояниях. В системе электропривода машина является частью элементов системы управления. Динамическое поведение АM может быть описано, используя динамическую модель АM. Динамическая модель рассматривает мгновенные эффекты переменных напряжений/тока, частоты статора и вращающего момента. В этой статье динамическая модель АM получена при помощи d и q переменных в синхронном вращении.
Асинхронный двигатель - простой электрический трансформатор, магнитная схема которого отделена воздушным зазором в две относительно подвижные части, одна проведение первичной и другой вторичной обмотки. Переменный ток подается на первичную обмотку из энергосистемы, индуцирует ток в противоположной вторичной обмотки закрыта через внешний импеданс. Относительное движение между основная и вторичная структура произведена электромагнитными силами, соответствующих мощности, таким образом, перемещаемых через воздушный зазор по индукции. Существенные признаки, которые отличают асинхронную машину от другого типа электрических двигателей является то, что вторичные токи создаются исключительно по индукции, как в трансформаторе вместо того, чтобы питание от постоянного тока возбудителя или других внешних источников питания, как и в синхронных и машин постоянного тока.
2. Эквивалентная схема - параметры эквивалентной схемы асинхронного двигателя крайне важны, рассматривая продвинутые методы контроля (т.е. Векторный Контроль). Бывает, что завод-изготовитель предоставляет также неверные параметры. Наиболее распространенные способы, с помощью которых можно вручную определить параметры асинхронного двигателя должны испытать двигатель без нагрузки и с блокированным ротором.
2.1 Испытание без нагрузки.
Испытание без нагрузки, как испытание разомкнутой цепи на трансформаторе, дает информацию о возбуждении. Оно выполнено, применяя постоянное номинальное напряжение на статоре при номинальной частоте. Машина будет вращаться с почти синхронной скоростью. Это испытание производится на основе эквивалентной схемы, представленной ниже.
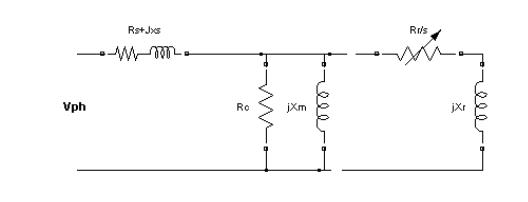
Выполняется следующий расчет:

2.2. Испытание блокировки ротора.
Испытание заблокированного ротора, выполняется как короткое замыкание трансформатора, предоставляет информацию об сопротивлении утечки и сопротивления ротора. Ротор остается на стенде по-прежнему, в то время как низкое напряжение на обмотках статора будет способствовать возникновению номинального тока. Необходимо измерить напряжение и мощность фазы. Поскольку нет вращения, скольжения, s=1, что дает нам следующую эквивалентную схему.
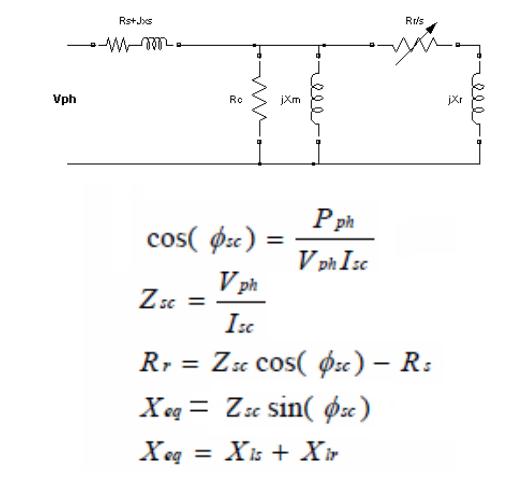
3. Dqo преобразование.
В электротехнике, прямой квадратурной нулю (DQ0) преобразование или нулевой прямой квадратурной (0DQ) преобразование называется математическое преобразование, которое используется для упрощения анализа трехфазных цепях. В случае сбалансированных трехфазных цепей, применение dqo преобразование уменьшает три переменного количества в два DC.Упрощенные вычисления могут тогда быть выполнены на этих мнимых величинах постоянного тока перед выполнением обратного восстановления фактического трехфазного результата переменного тока. Он часто используется для того, чтобы упростить анализ трехфазных синхронных машин или для упрощения расчетов для контроля трехфазных инверторов. Dqo преобразования, представленные здесь, чрезвычайно похожы на преобразование впервые предложеные в 1929 году RH Парка. На самом деле, dqo преобразования часто упоминается как преобразование Парка.
Dqo преобразование применяется к трехфазным токам, представленным ниже в матричном виде:

Обратное преобразование:
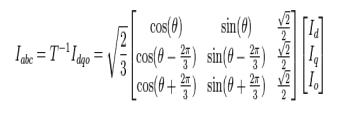
4. Описание энергосистемы Blockset.
Matlab / Simulink это симулятор системы, который не в состоянии управлять имитацией электрических цепей, поэтому для моделирования системы электрических цепей, питание, наборы блоков используются Simulink, в котором есть библиотеки электрических блоков и инструменты анализа, которые используются для преобразования электрических цепей в Simulink диаграмм. Электрические блоки электрических моделей таких как электрические машины, источники тока и напряжения, а также различные электрические элементы, силовые электронные ключи, разъемы, и датчики для измерения. При запуске моделирования Simulink необходимо использовать Pm Blockset и передает электрическую цепь в пространстве состояний представления с начальными условиями переменных состояний. Фактическое моделирование начинается после этого первоначального преобразования, это позволяет использовать широкое разнообразие с фиксированным шагом и переменным шагом алгоритма, доступные в Simulink. Как переменная временной шаг алгоритма работает быстрее, чем фиксированный момент времени методом, потому что ряд шагов в меньшей степени, эти алгоритмы используются для малых и средних систем, так и для крупных систем, содержащие большее количество территорий и/или силовых переключателей. Simulink группы могут быть использованы для отображения результатов моделирования или отправлены на рабочую область в ходе моделирования. Разнообразие функций и панелей инструментов MATLAB присутствуют для обработки и печати осциллограмм от сохраненных данных.
5. Модель асинхронного двигателя в SIMULINK.
Обобщенная динамическая модель асинхронного двигателя состоит из электрического подмодели по реализации трехфазных две оси (3/2)преобразованию с двумя осями напряжения статора и текущему вычислению, подмодель вращающего момента, чтобы вычислить развитый электромагнитный вращающий момент и механическую подмодель, нужно привести к скорости ротора.

Электрическая подмодель асинхронного двигателя трехфазовое к преобразованию напряжения с двумя осями достигнута, используя следующее уравнение.
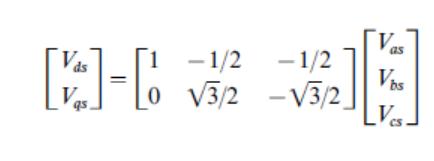
Где Vas, Vbs и Vcs являются трехфазные напряжения статора, в то время как Vds и VQS являются две оси вектора напряжения статора. Вращающий момент подмодели асинхронного двигателя в два-оси статор отсчета, электромагнитного T учитывая с помощью
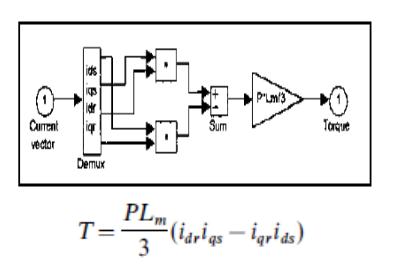
Механическая подмодель асинхронного двигателя от вращающего момента уравновешивает уравнения и пренебрежение вязким трением, скорость ротора ?o может быть получена следующим образом
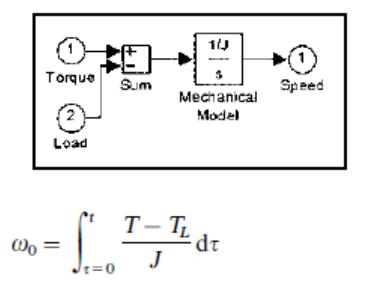
Где J - момент инерции ротора и нагрузки, и TL - вращающий момент нагрузки.
Подмодель текущей производительности статора.
Подмодель текущей производительности статора используется, чтобы вычислить амплитуду тока статора согласно следующему уравнение

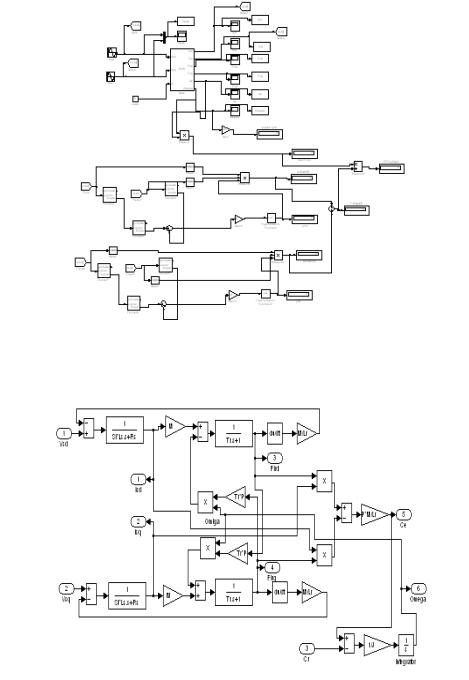
6. Результаты моделирования
У асинхронного двигателя, выбранного для исследований моделирования, есть следующие параметры:
Rs=1.5 Ом Rr=0.7 ОмL s=0.012 H Lm=0.1118 H
L r=0.1122 H J=0.054 кг м2
P=2 Ts=0.0546 нм
Tr=0.160 нм
Результаты моделирования для развитого вращающего момента, скорости, Vsd, Vrd, Ird, Irq представлены ниже.
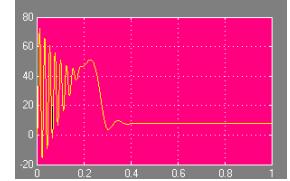
Вращающий момент
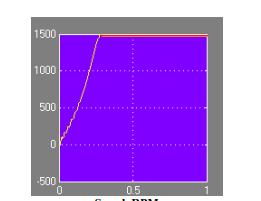
Скорость RPM


Скорость RPM
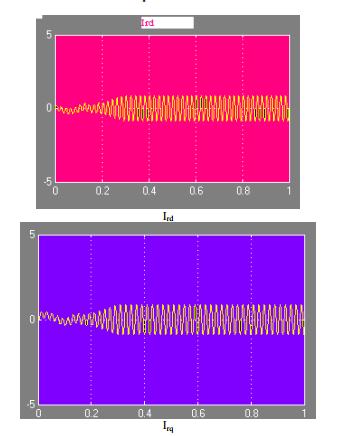
Выводы
SIMULINK - сильный пакет программ для исследования динамических и нелинейных систем. Используя SIMULINK, модель моделирования может, систематически усовершенствоваться начинаясь с простых подмоделей. Модель асинхронного двигателя может использоваться , так и для электропривода. Авторы полагают, что SIMULINK скоро станет обязательным инструмент для обучения и исследования электрических двигателей.
Список использованной литературы
1. G. J. Retter, "Matrix and Space-phasor theory of electrical Machines",Akademiai Kiado,udapest, 1987
2. D. O’Kelly and Simons, "Introduction to Generalised Electrical Machine Theory", McGraw- Hill, 1968.
3. Mohan, N. "Advanced Electric Drives. Analysis, Control and Modeling using Simulink®", MNPERE, 2001
4. Adkins, B. "The General Theory of [5] P. Vas, "The control of AC machines" Oxford Univ., 1990.
5. P.C. Krause, "Electric machines", prentice Hall, 1985. Hoang Le-Huy.. Modeling and Simulation of Electrical Drives using MATLAB/Simulink and Power System Blockset. IEcon’01: The 27th Annual Conference of the IEEE Industrial Electronics Society.
6. Hosea M.E., Shampine L.F. Analysis and implementation of TRBDF2 // Applied Numerical Mathematics. Vol. 20. 1996. № 1-3. P. 21-37.
7. Czeslaw T. Kowalski, Jacek Lis, Teresa Orlowska- Kowalska. FPGA implementation of DTC Control Method for the Induction Motor Drive. EUROCON 2007 : The International Conference on "Computer as a Tool" Warsaw, Sept. 9-12,2007
8. R.K.Rajput, "Electrical Machines,"first edition, New York: McGraw- Hill, 1993, pp. 352-353
9. R.Krishnan, "Electric Motor Drives Modeling, Analysis and Control", first edition, 2001Prentice-Hall International, Inc. Upper Saddle River, New Jersey 07458.
10. Krause, P. C., "Simulation of symmetrical induction machinery", IEEE T rans. Power apparatus Systems, Vol. PAS-84, No. 11, pp. 1038–1053 (1965)
11. Ghani, S. N., "Digital computer simulation of three-phase induction machine dynamics a generalized approach", IEEE T rans Industry Appl., Vol. 24, No. 1, pp. 106–114 (1988)
12. Wade, S., Dunnigan, M. W. and Williams, B. W., "Modeling and simulation of induction machine vector control and rotor resistance identification", IEEE Trans. Power Electronics, Vol. 12, No. 3, pp. 495–505 (1997)