Русский   English
ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

Синхронні двигуни з постійними магнітами (СДПМ) використовуються в широкому діапазоні потужностей від мВт до сотень кВт. Так само були прийняті спроби застосувати постійні магніти до двигунів потужністю більше 1 МВт. Таким чином, застосування СДПМ можливо у великій кількості областей, від крокових моторів для наручних годинників і промислових приводів для верстатів до великих СДПМ для корабельних силових установок [1]. Основними сферами застосування синхронних двигунів з ПМ є [2]: промисловість, громадське застосування, офісне обладнання [3], засоби пересування, оборонні сили, аерокосмічна галузь, медичне та оздоровче обладнання, електроінструмент, системи відновлюваної енергії, обладнання для досліджень і експериментів.

Особливістю СДПМ є наявність постійних магнітів в роторі, які генерують постійне магнітне поле на відміну від короткозамкненого ротора в асинхронних машинах, що дає ряд переваг для розробників двигуна, виробників і кінцевих споживачів. Ці переваги включають компактну форму з високою щільністю крутного моменту і меншою вагою, високий статичний момент на великому діапазоні швидкостей, низький момент інерції ротора, високі динамічні характеристики, високу ефективність роботи за малих теплових втрат роторі, низькі пульсації моменту, більш високу експлуатаційну надійність по порівнянні з двигунами постійного струму, високий cos φ.

Недоліками СДПМ є зростаючі ціни на рідкоземельні матеріали через певні економічні чинники на світовому ринку, хоча недавні відкриття рідкоземельних магнітів в США та інших країнах може значно вплинути на дану ситуацію в майбутньому, наявність противо‐ЕРС, створюваного постійними магнітами, обов'язкова наявність датчика положення ротора для застосування в поле‐орієнтованому керуванні.

1. Актуальність теми

Основним з перерахованих вище недоліків, є датчик положення, який вразливий до електромагнітних перешкод, має обмежений діапазон робочих температур, збільшує габарити двигуна, погіршує загальну експлуатаційну надійність приводу.

Усунення електромеханічного датчика здешевлює апаратну частину, зменшує складність установки системи (відсутність додаткових кабелів), знижує інерційність системи і чутливість приводу до шумів, збільшує робастність і надійність.

Загалом методи оцінки положення валу СДПМ можна розділити на:

  1. Неадаптивні:
    • Оцінка на основі вимірюваних напруг і струмів статора;
    • Оцінка на основі вимірюваних напруг і струмів статора;
    • Оцінка на основі проти‐ЕРС.
  2. Адаптивні:
    • Оцінка на основі системи з адаптивною моделлю;
    • Оцінка за допомогою спостерігачів стану.
  3. Інжекція сигналів: метод оцінки позиції ротора за допомогою введення високочастотної складової в напругу (струм) статора і обчислення ефекту анізотропії машини на відповідну складову напруги (струму) статора.
  4. Штучний інтелект: представлений нейронними мережами, системами нечіткої логіки і нечіткими нейронними мережами. Дані методи не потребують математичної моделі приводу, мають хороші властивості зниження шумів, можуть бути легко розширені і модифіковані, відрізняються робастностью до варіацій параметрів і низькими вимогами до обчислювальних потужностей [4].

Магістерська робота присвячена дослідженню актуальної наукової задачі бездатчикового векторного керування СДПМ. Отримані результати будуть перевірені шляхом математичного моделювання в пакеті MATLAB\Simulink.

2. Огляд досліджень і розробок

Бездатчикове керування СДПМ є перспективним напрямком для досліджень, що підтверджується роботами учених по всьому світу. Розробки даної теми почалися ще в 80‐х роках ХХ століття. Особлива увага даній темі приділяється в Китаї (Jinsong K., Xiangyun Z., Ying W.), Японії (Morimoto S., Kawamoto K., Sanad M., Ichikawa S., Chen Z.), Індії (Benjak O., Mishara A., Mahajan V., Agarwal P.). Так само ведуться дослідження в США та європейських країнах (Schroder D., Schaffner C., Li Y.). Серед вітчизняних дослідників даною темою займаються: Білецький Ю.О., Яровий Г.І., Щур І. З., Аніщенко Н.В.

3. Математичний опис СДПМ

Нижче представлений математичний опис СДПМ в природній трифазній системі координат. Остання може бути трансформована в інші, наприклад, за допомогою перетворення Парку – у систему координат, що обертається, орієнтовану за потокозчепленням ротора d, q або в двофазну ортогональну нерухому α‐β (с помощью преобразования Кларка)

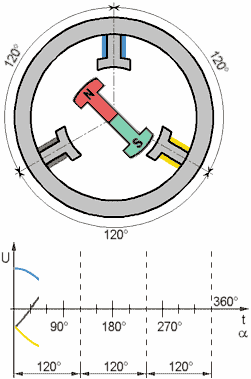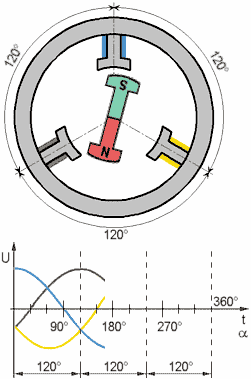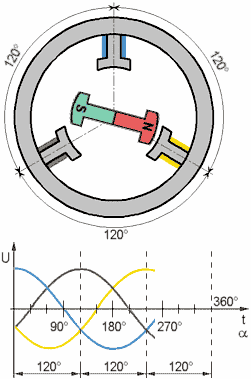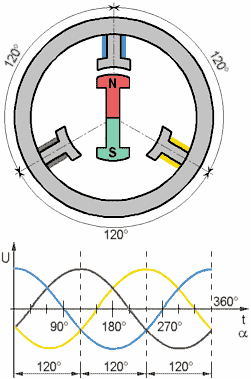
Рисунок 3.1 – Спрощена модель СДПМ (GIF анімація, 12 кадрів, 7 ітерацій, 22 кб)
Рисунок 3.1 – Спрощена модель СДПМ (GIF анімація, 12 кадрів, 7 ітерацій, 22 кб)

Рівняння балансу напруги статора 3х фазного симетричного СДПМ у матричній формі:


де:

ua, ub, uc – миттєві значення фазних напруг статора,

Rs – активний опір статорної обмотки,

ia, ib, ic – миттєві значення фазних струмів статора ,

ψa, ψb, ψc – потокозчеплення обмоток статора.

Фазні потокозчеплення можуть бути представлені у виді:


де:

ψm(θ) – потокозчеплення постійних магнітів,

Lxx(θ) – власна індуктивність обмотки x,

Lxy(θ) – взаємна індуктивність обмоток x i y.

Індуктивності обмоток статора визначені як функції кута повороту ротора:


де:

Ls(θ) – середне значення власної індуктивності кожної обмотки статора.

Lm(θ) – амплітуда флуктуації власної індуктивності ї взаємної індуктивності обмоток статора із‐за зміни кута повороту ротора.

Ms(θ) – середне значення взаємної індуктивності між статорними обмотками.

Потокозчеплення постійних магнітів визначається як:


Для обчислення електромагнітного моменту використовується рівняння, що складені відповідно закону Ленца:


де Zp число пар полюсів.

Використовуючи перетворення Парка можна перейти до системи координат, що обертається d, q, яка орієнтована за потокозчепленням ротора.

Рівняння балансу напруги статора:


де:

ud, uq, u0 – проекції вектору напруг на вісі d,q відповідно, напруга нульової послідовності.

id, iq, i0 – проекції вектору струму на вісі d,q відповідно, струм нульової послідовності.

Ld = Ls + Ms + 3/2 * Lm – індуктивність статору по d - вісі.

Lq = Ls + Ms - 3/2 * Lm – індуктивність статору по q - вісі.

L0 = Ls - 2Ms – індуктивність статору нульової послідовності.

ωr – кутова механічна швидкість обертання ротора.

Рівняння моменту у системі координат d, q матиие вид:


Найбільш простими, в плані вимог до обчислювальному пристрою й простоті наладки, є неадаптивні методи ідентифікації. Але вони показують гірші результати в порівнянні з адаптивними методами, які в свою чергу складніше налаштовувати і вони вимагають більше обчислювального часу. Далі наведені неадаптивний метод на основі струмів і напруг статора і метод на основі АСЕМ.

4. Методи ідентифікації

4.1 Оцінщик на основі виміряних напруг та струмів статора

У даному підходsі використовується модель двигуна в системі координат, що обертається d, q. Загалом, залежність між d, q складовими в обертовій та стаціонарній системі координат може бути виражена як [5-7]:


де верхні індекси "r" та "s" використовуються для позначення обертовою і стаціонарної системи координат, відповідно. [C1] – матриця коефіцієнтів перетворення Кларка:


Підставляючи u i i замість х в рівняння (2) і виконавши перетворення отримаємо:


Залежність між трифазними і ортогональними змінними в нерухомій системі координат визначаються як:


де:


Підставляючи u и i замість х в рівняння (4) і виконавши перетворення отримаємо:


З рівнянь (2) і (3) можна отримати наступні рівняння:


Перетворюючи ортогональні змінні в трифазні використовуючи рівняння (5) і (7) можна отримати вираз для знаходження кута порота ротора:


де:


Таким чином положення ротора може бути отримано за допомогою напруг і струмів статора і швидкості ωr,яка в свою чергу, так само може бути обчислена за допомогою напруг і струмів статора. Для цього використовуються рівняння (6) і (7), в яких замість d, q складових підставляємо трифазні, згідно рівнянь (5) і припускаючи, що Lq = Ld = Ls. Отримаємо наступний вираз для обчислення швидкості ωr:


де:


На рис. 4.1 представлені графіки перехідних процесів двигуна і помилка оцінювання швидкості валу СДПМ.

Рисунок 4.1 – Перехідні процеси при роботі двигуна (а), помилка оцінювання швидкості валу СДПМ (б)
Рисунок 4.1 – Перехідні процеси при роботі двигуна (а), помилка оцінювання швидкості валу СДПМ (б)

З графіків рис. 4.1 видно, що помилка оцінювання швидкості не перевищує 10 рад/с. З недоліків можна відзначити погану працездатність методу на швидкостях, близьких до нульових, що пов'язано з низькими значеннями струмів.

4.2 Оцінювач на основі адаптивної системи з еталонною моделлю (АСЕМ)

Далі буде описана АСЕМ яка використовує дві моделі для обчислення потокозчеплення СДПМ. Одна модель є еталонною, інша – що настроюється. Структурна схема АСЕМ наведена нижче.

Рисунок 4.2 – Структурна схема АСЕМ
Рисунок 4.2 – Структурна схема АСЕМ

Рівняння еталонної моделі на основі математичного опису СДПМ в нерухомій системі координат представлені нижче [8-10]:


Дані два рівняння відповідають моделі напруги статора, яка не містить кут повороту ротора і являє собою еталонну модель.


Рівняння (9) і (10) являють собою струмову модель, яка містить кут повороту ротора і відповідно представляє собою модель, що настроюється. Вихід цих двох моделей порівнюється в механізмі адаптації для оцінки параметра, який налаштовує адаптивну модель таким чином, щоб помилка між виходами цих моделей прагнула до нуля.

Механізм адаптації використовує помилку кута Δθ як коригувальну інформацію для обчислення регульованого параметру θ в адаптивній моделі:


Адаптація виконується за допомогою ПІ коректора:


Моделювання виконувалось у наступних режимах: розгін до номінальної швидкості на холостому ході, накид номінального навантаження, гальмування до нульової швидкості. Для моделювання використані наступні параметри двигуна:


Коефіцієнти ПІ коректора було визначено експериментальним шляхом.Перехідні процеси та помилка оцінювання приведені на рис. 4.3.


Рисунок 4.3 – Перехідні процеси в різних режимах роботи (а) та різниця між дійсним кутом та обчисленим (помилка оцінювання) (б)

Висновки

  1. Отримання системи бездатчикового електроприводу і усунення електромеханічного датчика здешевлює апаратну частину, зменшує складність установки системи (відсутність додаткових кабелів), знижує інерційність системи і чутливість приводу до шумів, збільшує робастність і надійність.
  2. Проведений аналіз досліджень і розробок з даної теми показав наявність великої кількості методів ідентифікації кута повороту ротора СДПМ. З аналізу випливає, що вітчизняні публікації не пропонують розгорнутого та структурованого опису методів, а також рекомендацій до їх використання. Це призводить до необхідності проведення додаткових досліджень, чому і присвячена дана магістерська робота.
  3. Моделювання показало, що неадаптивний метод ідентифікації кута заснований на напругах і струмах є працездатним тільки на високих швидкостях і під навантаженням. Це пов'язано з великими струмами, що протікають в обмотках статора, які необхідні для обчислення кута і швидкості. Помилка оцінювання швидкості не перевищує 10 рад/с. На низьких швидкостях даний метод показує себе непрацездатним. Так само, можна відзначити високу чутливість до зміни параметрів двигуна. З переваг даного методу можна відзначити простоту реалізації і відсутність необхідності налаштування.
  4. Моделювання АСЕМ показало, що розроблена система має характеристики аналогічні характеристикам системи з електромеханічним датчиком положення ротора. З рис. 4.3 видно, що помилка оцінювання не перевищує 0.005 рад і збільшується при збільшенні моменту на валу. Таким чином, АСЕМ дозволяє вирішити задачу оцінки кута повороту ротора в різних режимах роботи двигуна. Результати моделювання показали, що розроблена система дозволяє отримати діапазон регулювання швидкості до 1:50. Недоліком методу є відсутність методики вибору коефіцієнтів коректора.

Так як на момент написання даного реферату написання магістерської роботи ще не завершено, на даному етапі розглянуті неадаптивні і частина адаптивних методів ідентифікації кута повороту ротора СДПМ. Надалі планується провести дослідження і математичне моделювання найбільш перспективних методів ідентифікації, таких як: спостерігачі стану, інжекція сигналів і штучний інтелект. Остаточне завершення магістерської роботи: січень 2015 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Список використаних джерел

  1. Fracchia M., Sciutto G. Cycloconverter Drives for Ship Propulsion. Symp on Power Electronics, Electr Drives, Advanced Electr. Motors SPEEDAM’94, Taormina, Italy. – 1994. – pp. 255G260.
  2. Gieras J. F. Permanent Magnet Motor Technology / J. F. Gieras, M.Wing. – 2002. – New York. – p. 611.
  3. Jabbar M.A., Tan T.S., Binns K.J. Recent developments in disk drive spindle motors. Int Conf on Electr Machines ICEM’92, Vol. 2, Manchester, UK, 1992, pp. 381-385.
  4. Benjak O. Review of Position Estimation Methods for IPMSM Drives without a Position Sensor Part I: Nonadaptive Methods / O. Benjak, D. Gerling // XIX International Conference on Electrical Machines – 2010. – pр. 1-6.
  5. Hoque M.A. Speed and Position Sensorless Permanent Magnet Synchronous Motor Drives / M.A. Hoque, M.A. Rahaman // IEEE Anadien Conference on Electrical and Computer engineering, CCECE – 1994. – pp. 689-692.
  6. Jabbar M.A. Sensorless Permanent Magnet Synchronous Motor Drives / M.A. Jabbar, M.A. Hoque, M.A. Rahman // Canadian Conference on Electrical and Computer Engineering, CCECE – 1997. – pp. 878-883.
  7. Johnson J. P. Review of Sensorless methods for Brushless DC / J. P. Johnson, M. Ehsani and Y. Guzelgunler // IEEE Industry Applications Conference, IAS, Vol. 1 – 1999. – pp. 143 – 150.
  8. Vesely L. Sensorless Control for Synchronous Motors // L. Vesely, P. Zbranek // International Conference on Autonomous and Intelligent Systems (AIS) – 2010. – p. 1-5.
  9. Mishara A. MRAS Based Estimation of Speed in Sensorless PMSM Drive / A. Mishara, V. Mahajan, P. Agarwal // IEEE Fifth Power India Conference. – 2012 – p. 1- 5.
  10. Ichikawa S. Sensorless Control of an Interior Permanent Magnet Synchronous Motor on the Rotating Coordinate Using an Extended Electromotive Force / S. Ichikawa, C. Zhiqian, M. Tomita, S. Doki // Industrial Electronics Society, 2001. IECON '01. The 27th Annual Conference of the IEEE (Volume:3). – Denver. – 2001. – pp. 1667 – 1672.