Введение

Байесовская сеть (или байесовская сеть доверия, сеть доверия, deep belief network) – относительно новая и быстроразвивающаяся архитектура, нашедшая применение в различных областях искусственного интеллекта. Такое широкое распространение данной модели связано с ее гибкостью и возможностью применения различных модификаций, позволяющих приспособить сеть к условиям конкретной задачи.

Целью написания данной статьи является изучение способов представления байесовских сетей доверия для решения задачи распознавания образов. Необходимо решить следующие задачи: рассмотреть сети доверия с позиции графических моделей и нейронных сетей, изучить методы обучения сетей доверия, выявить найболее удачные подходы к представлению байесовских сетей для решения задачи распознавания образов. Актуальность поставленных задач объясняется важностью в современном мире решения задачи распознавания образов и широким рапространением байесовских сетей доверия.

Задача распознавания образов

Задача распознавание образов – это задача отнесения исходных данных к определенному классу объектов с помощью выделения существенных признаков, характеризующих эти данные, из общей массы несущественных данных [1].

Распознавание образов является одной из фундаментальных проблем в теории интеллектуальных систем, а также имеет глубокое практическое значение. Часто термин «распознавание» заменяется термином «классификация». Во многис случаях они рассматриваются как синонимы, но не являются полностью взаимозаменяемыми. Каждый из них имеет свои сферы применения, а интерпретация обоих терминов часто зависит от специфики конкретной задачи.

Байесовские сети как графическая модель

Байесовские сети доверия – это графическая модель, представляющая собой множество переменных и их вероятностных зависимостей. Формально, данная сеть представляет собой направленный ациклический граф, где вершины – это переменные, а дуги – отношения условной зависимости между этими переменными [2]. Данная модель нашла свое применение в экспертных системах, где может использоваться, например, для определения болезни пациента по наличию или отсутствию у него симптомов, основываясь на данных о зависимости между симптомами и болезнями. На рис. 1 представленная такая сеть, показывающая как зависят друг от друга кашель, нахождение в задымленном помещении и заболевание гриппом. В данном случае кашель – это наблюдаемый эффект, а дым в помещении и грипп – это ненаблюдаемые и независящие друг от друга причины.

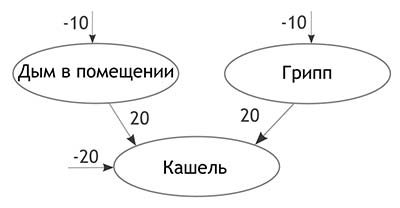Рисунок 1 – Сеть доверия для определения причин кашля

Для логического вывода на такой графической вероятностной модели используется алгоритм распространения доверия, предложенный Джудой Перлом (Judea Pearl). Но данный алгоритм может быть использован только тогда, когда известны вероятностные зависимости между переменными. Это накладывает ограничения на области применения байесовских сетей доверия. Данный недостаток можно с успехом обойти, если посмотреть на сети доверия не как на графическую модель, а как на нейронную сеть.

Байесовские сети доверия как нейронная сеть

Если абстрагироваться от деталей, то сети доверия очень сильно схожи с многослойными нейросетевыми архитектурами, особенно с многослойными персептронами. Так, например, вычисления условной вероятности активации переменной в ответ на собственное индуцированное локальное поле в байесовских сетях определяется следующей функцией:

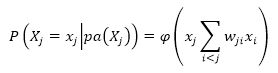
где xj – это переменная, определяющая сеть доверия, а wj – вероятностная зависимость между двумя переменными. А функция активации нейрона в многослойном персептроне определяется следующим выражением:

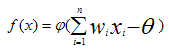
где xj – это элемент вектора входных сигналов, wj – синаптический вес, соединияющий пару нейронов, ϑ – некоторое смещение, или собственное значение нейрона.

Как видим, эти формулы очень похожи. Их сходство состоит в том, что в обоих случаях текущее значение некоторого элемента зависит от состояний связанных с ним элементов. Различие как раз и заключается во множестве этих элементов.

Проблема с сетями доверия также состоит в том, что очень сложно получить апостериорное распределение по всем возможным конфигурациям скрытых элементов сети, а в случае с сетью, имеющей миллионы параметров, это практически невозможно. Обучение было бы простым, если бы удалось получить достоверную выборку по апостериорному распределению скрытых состояний по наблюдаемым данным [2]. Эта процедура является достаточно сложной в том числе и в следствии «эффекта объяснения», который заключается в том, что две причины (элементы скрытого слоя сети доверия), являющиеся независимыми, могут быть зависимыми для того, кто наблюдает некоторый эффект, который зависит от обеих этих причин. Таким образом, чтобы получить апостериорное распределение даже в первом скрытом слое сети, требуется интегрировать по всем возможным конфигурациям скрытых переменных. А как было описано выше, эта процедура в сложных сетех становится невозможной.

Единственное решение представляется в использовании процедуры обучения без учителя, которая бы максимизировала нижний порог логарифмической вероятности входа [3]. Обученная таким образом модель может быть использована как многослойная нейронная сеть обратного распространения. Чтобы не злоупотреблять терминологией, результирующая нейронная сеть также называется байесовской сетью доверия.

Сети доверия как стек ограниченных машин Больцмана

Можно оптимизировать использование байесовской сети доверия, выполнив некоторые модификации в архитектуре сети. Если заменить в ацикличном направленном графе сети доверия все связи на симметричные, то получится машина Больцмана, изобретенная Хинтоном и Сейновски в 1983 г. А ограничив некоторым образом соединения, добъемся упрощения в обучении данной архитектуры. Это ограничение состоит в том, чтобы обучать сеть по одному слою скрытых элементов за раз. Позднее сеть будет доучена уже со всеми слоями сразу, но для предобучения такая методика является очень эффективной, так как все элементы в одном скрытом слое условно независимы для данных видимых состояний. Таким образом, можно быстро получить достоверную выборку из апостерионого распределения когда дан вектор входных данных. Описанная выше модификация машины Больцмана называется ограниченной машиной Больцмана (рис. 2), и если рассматривать многослойную сеть доверия как стек таких машин, то можно обойти все описанные выше проблемы в обучении сетей доверия [4].

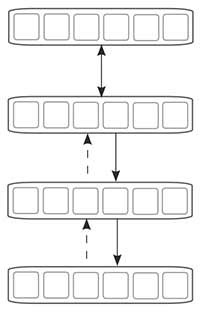Рисунок 2 – Модель ограниченной машины Больцмана

Теперь такая модель может быть легко обучена «жадным» алгоритмом обучения без учителя послойно, начиная с первого слоя, с постепенным добавлением следующих слоёв в процедуру обучения, как стоительных блоков в строящемся доме [5]. При таком подходе даже возможна комбинация с использованием процедуры обучения с учителем.

Представление байесовской сети доверия в виде стека машин Больцмана представляет собой прекрасную модель для решения задачи распознавания образов. Именно такая архитектура позволит обучать сложные сети с огромным множеством классификационных признаков на большом количестве примеров. Также благоприятным фактором для использования именно такой модификации модели служит тот факт, что в процедуре обучения без учителя, которая используется при обучении, используются немаркированные данные (unlabeled data), которые составляют большую часть примеров для обучения в распознавании образов. При этом гибкость алгоритма обучения позволяет обучать сеть на множеcтве маркированных данных.

Стоит также отметить, что в случаеиспользования процедуры обучения с учителем представляетсяэффективной возможность использования метода опорных векторов, который позволит привести обучаемое множество к требуемому виду для дальнейшего обучения.

Выводы

Рассмотрены разные подходы к представлению байесовских сетей доверия, что позволяет максимально эффективно использовать даннух архитектуру для решения задачи распознавания образов. Было выяснено, что представление сети доверия с помощью ограниченной машины Больцмана позволяет упростить процедуру обучения. Данные выводы требуют дальнейших экспериментов и подтверждения на практике.

Литература

[1] Задача распознавания образов. Электронный ресурс. Режим доступа: http://life-prog.ru/view_zam2.php?id=269&cat=4&page=9
[2] С. Хайкин. Нейронные сети: полный курс, 2-е издание, : Пер. с англ. – М.: Издательский дом «Вильямс», 2006. – 1104 с.
[3] Geoffrey Hinton. NISP tutorial on deep belief nets. – Canadian Institute for Advanced Research, Department of Computer Science, University of Toronto, 2007 – 100 p.
[4] Abdel-rahman Mohamed, Geoffrey Hinton, Gerald Penn. Understanding how Deep Belief Nets perform acoustic modeling. – ICASSP, 2012 – 4 p.
[5] Rasmus Berg Palm. Prediction as a candidate for learning deep hierarchical models of data. – Technical University of Denmark, 2012 – 80 p.
[6] Yoshua Dengio. Learning Deep Architectures for AI. – Université de Montréal, 2009 – 56 p.