Резюме

Машинное распознавание речи является важным объектом научных исследований уже на протяжении пятидесяти лет. Не смотря на достигнутый за последние годы значительный прогресс в этой области, качество разработанных систем распознавания речи все еще далеко от того, что умеет человек. Распознавание и понимание речи является важнейшей проблемой распознавания образов и искусственного интеллекта, и для ее решения разработаны многочисленные методы – оригинальные или адаптированные.

Среди большого количества моделей, предлагаемых для решения проблемы распознавания речи, имеются нейронные сети, занимающие в течении последних десяти лет заметное место среди инструменов для решения сложных задач классификации и распознавания образов, которые в точности находим в распознавании речи.

В этой статье мы протестируем новую методику распознавания речи, основанную на использовании нейронной сети как модели распознавания и байесовских методов для обучения этой модели.
Ключевые слова: Байесовские методы, нейронная сеть, метод Монте Карло, контрольная выборка, TIMIT, метод обратного распространения ошибки, распознавание речи, распределение Гаусса.

Введение

Байесовские методы применялись в последние годы к нейронным сетям разными авторами, в частности в работах МакКея (1992 а, б), Нила (1992, 1994, 1996), Бунтин и Вейдженеда (1991), Бишопа (1995), и наиболее новых работах Фрейта (1998, 2000) и Ветари (1999). Вейдженед, Нил и МакКей показали, что байесовские методы для обучения нейронных сетей могут принести многочисленные преимущества, так как не требуется ограничивать размер сети чтобы избежать переобучения; количество нейронов в скрытом слое может достигать бесконечности; единственный фактор, который может ограничить размер сети – это возможности используемых компьютеров и имеющееся время для выполнения требуемых расчетов. Так как используемые параметры для расчета требуемых интегралов происходят из вероятностной выборки, то чтобы узнать требуемые параметры, необходимо вмешаться в распределения других параметров.

В целом, невозможно рассчитать эти интегралы аналитически, и многочисленные подходы были предложены для выполнения их расчетов. Но либо эти подходы очень сложно применить, либо они используют аппроксимацию, которая может исказить результаты.

В своей работе в 1994 Нил использует методы Монте Карло в связке с скрытыми Марковскими моделями для вычисления требуемых на разных этапах интегралов. Эти вычисления очень сложные и требуют много времени.

МакКей предложил аппроксимацию, базирующуюся на гауссовых гипотезах о апостериорных вероятностях. Благодаря этим гипотезам, вычисление интегралов упрощается и может быть выполнено более или менее просто. Эти гипотезы иногда бывают спорными, в частности для задачи классификации. Тем не менее, благодаря этим аппроксимациям, вычисления упрощаются настолько, что байесовский подход становится употребим на практике.

В этой статье мы собираемся интегрировать в байесовских методах для расчета разных интегралов выборку по значению, которая является техникой Монте Карло.

1. Обучения байесовскими методами

Использование теоремы Байеса позволяет предложить байесовскую формулировку обучения, которая является наиболее общей и которая может быть применима к исследованиям любых типов моделей, если только они представляются множеством параметров по которым можно сделать предположение о распределении. Мы описываем здесь принцип интуитивного подхода, и также показываем его применение в рамках нейронных сетей.

Пусть X будет набором переменных. Пусть D будет базой примеров, объединяющей наблюдения и эти переменные. Мы ищем способ придать вес этим наблюдением с помощью модели M, выбирая из семьи моделей М. Единожды выбранная, эта модель будет предсказывать будущие наблюдения.

Чтобы использовать байесовское обучение в этой проблеме, достаточно остановиться на том, что мы ищем приближение моделью m распределения вероятности P(X). Оно не ограничивается общим подходом, так как в детерминированной модели классификации предсказание может быть описано распределением частных вероятностей.

Также предположим, что запись P(M,D) имеет смысл. Другими словами, говоря, что модель М может быть представлена параметрами, и что мы может определить распределение вероятностей по этим параметрам (для модели нейронных сетей параметры будут весами сети).

По определению условной вероятности, имеем:

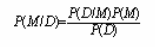
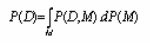
2. Байесовские методы обучения нейронных сетей

Классическое обучение эффективно в нахождении вектора весов, который минимизирует функцию издержек или ошибки.

В байесовских методах, все параметры, особенно веса сети, рассматриваются как случайные величины распределения вероятностей.

Обучение нейронной сети в таком случае состоит из определения распределения вероятностей весов для обучающей выборки: присваиваем весам фиксированные априорные вероятности, и сразу же, когда данные для обучения становятся видимыми, эта априорная вероятность трансформируется в апостериорную вероятность благодаря теореме Байеса. Так как если D представляет обучающее можество, р(w) это удельный весс априорной вероятности весов , р(D|w) – удельный вес вероятности наблюдения известных значений весов сети и Р(w|D) – апостериорная вероятность того, что ищем определенное значение. Итак, теорема Байеса гласит:

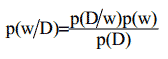
3. Последовательное обучение нейронных сетей.

Чтобы выполнить последовательное обучение, предположим, что эволюция нейронной сети во времени будет представлена двумя уравнениями, первое описывает изменение весов в сети, второе описывает нелинейное отношение входов к выходам:

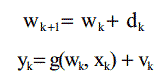
Надо учитывать, что при последовательном моделировании методом Монте-Карло переменные искажены шумом v, распределение вероятности шума определяется пользователем. В нашем случаее, шум моделируется гауссовским распределением со средним ноль и ковариантностью R. Шум переменных не кореллируется с весами сети и начальными условиями. (Фрета 1998, Гордон 1993)

Мы предполагаем, что изменение весов сети зависит от их предыдущих значений и стохастической составляющей d(k). Эта составляющая симулируется гауссовским распределением со средним нулем и ковариантным Q, однако, другие распределения также могут быть использованы.

Сейчас теорема Байеса в формулировке (1) может быть записанна как (4)

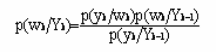
Формула (4) отвечает оптимальному решению проблемы, но к сожалению, она привносит многомерное интегрирование (так как используемые параметры происходят из распределения вероятностей, для того чтобы узнать параметр расчета интегралов требуется вмешаться в распределения других параметров). Это интегрирование является источником большей части практических сложностей. В большинстве применений, аналитическое решение невозможно, поэтому мы должны прибегнуть к другим методикам, таким, чтобы гауссово приближение (МакКэй 1999) и методы Монте Карло (Бишоп 1995, Фрета 1998, Нил 1996), в нашем случае позволили использовать выборку по значимости для расчета разных интегралов.

4. Выборка по значимости

Большинство подходов могут быть использованы для увеличения эффективности методов Монте Карло. Среди них существует техника выборки по значимости, являющейся наиболее удобной и наиболее эффективной по сравнению с другими техникой уменьшения дисперсии. (Фрета 1998, Гулль 1988, Мюллер 1991). Можно сказать, что эта техника является эффективным инструментом для вычисления вероятностных событий, ради которого мы и применяем байесовские методы для обучения нейронных сетей.

Фундаментальная идея, заложенная в методах Монте Карло, заключается в том, что вместе взятые взвешенные образцы из функции постериорной плотности весов нейронной сети используются для отслеживания интегрирования, включенного в процесс интерференции дискретных сумм. (рис. 1). Мы используем следущее приближение Монте Карло:

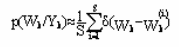
Рисунок 1 – Процесс выборки Монте Карло

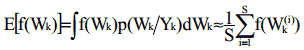
В случае методов Монте Карло, веса взяты из функции плотности вероятности р(Wk/Yk), но достижение базовой вероятности ведет нас к увеличению числа образцов S, которые будут очень дорогими по фактору времени. Тем не менее, можно преодолеть эту трудность техникой выборки по значимости. Она позволяет нам взять веса функции модифицированной плотности π(Wk/Yk) и ассоциировать с каждым образцом значение (q) называемое пропорцией важности, такой что: (Ветари 1998, Ветари 2000).

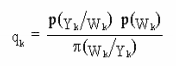
Для того чтобы вычислить последовательно оценку функции плотности π (за время k) без модификации симулируемых предыдущих состояний (Wk-1), мы применяем функцию плотности:

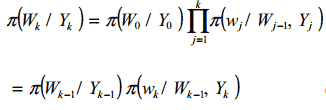
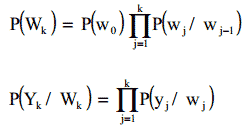
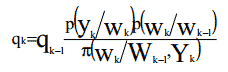
Чтобы реализовать этап пересемплирования, вместе определяем: Образец с наибольшим выбранным значением q.

Использование результата Конга (Конг 1994), который требует чтобы ресемплирование было выполнено только если размер эффективной выборки Nef f был выше фиксированного порога. Размер эффективной выборки определен как:

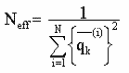
Сейчас мы применяем следующую функцию плотности вероятности:

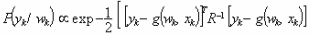
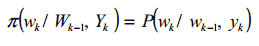
Этот выбор функции обоснован и другими исследователями. Однако, плотность:

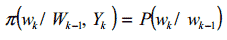
Сейчас, можем выбрать начальные веса и пропорции важности Приора с:

5. Приложение к распознаванию речи

Для валидации этой техники на распознавании речи, используем американскую базу данных ТИМИТ, которая является известной базой для обеспечения фонетическими акустическими данными речи для разработки и обучения автоматической системы распознавания речи.

Она содержит записи 630 америанских дикторов, разделенных на 8 «региональных диалектов» («рд1», «рд2») и говорящий каждый по 10 фраз. (Лоншап 1991а, 1991б).

5.1 Использованный корпус

Наши тести были выполнены на 18 фонемах выбраных из базы данных ТИМИТ: 6 фрикативов, 6 гласных и 6 взрывных звуков.

Система предоставляет важное количество для обработки:
- Каждая фонема встречается во фразе 2 раза (один раз для обучения и другой для теста)
- Формат хранения данных (дабл с плавающей точкой, 32 бита)

5.2 Архитектура использованной нейронной сети

Для валидации нашей техники, выбрали многослойную нейронную сети (МЛП) как модель распознавания, за их общеизвестную способность быть хорошим всеобщим апроксиматором и классификатором.

Мы тренировали нейронную сеть на разных архитектурах, и с разными параметрами чтобы найти лучшую модель, которая нам даст максимальную плотность постериорной вероятности весов и ее, согласно принципу максимума апостериор (МАР). Принимаем следующие предположения:

- Веса

Начальные значения весов сети выбраны из функции плотности гауссовой вероятности … Для двух распределений берем среднее ноль и дисперсию 1 (элементы диагонали матрицы начальных весов).

- Шум

Предполагаем что шум в симулируется гауссовым распределением со средним нулем и R = 0,7 (элементы диагонали ковариационной матрицы), подобно тому как d симулируется гауссовым распределением со средним нулем и ковариантностью равной q.

- Образцы

Выбрали n=500 образцов для симуляции Монте Карло и для 100 итераций и k=200.

5.3 Интерпретация результатов.

Чтобы иметь возможность протестировать эффективность нашей техники обучения, сравним ее с наиболее классическим алгоритмом обучения нейронных сетей, алгоритмом «обратного распространения ошибки».

Принимаем во внимание три ключевых фактора успеха в неважно каком процессе обучения: время обучения, процент распознавания, минимизация ошибки.

Следуем следующим сокращениям: N1 – число нейронов во входном слое, N2 – число нейронов в скрытом слое, N3 – число нейронов в выходном слое.

- Обучение

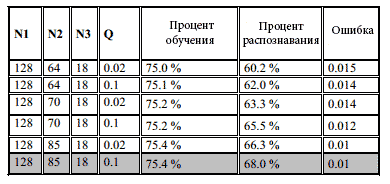
Хотим исправить параметры сети (архитектуры N1=128, N2=64, N3=18, максимальное число итераций и ошибка заданы) чтобы иметь возможность сравнить результаты двух методов: Мы обучили сеть и записали результаты в рис. 2:

Рисунок 2 – Сравнение среди реализованного числа итераций

Рис2 иллюстрирует эффективность обучения байесовскими методиками, ожидающие фиксированную минимальную ошибку и максимум своего процента распознавания (75,4%) без исчерпания максимального числа итераций, наоборот, обучение методом обратного распространения ошибки израсходовало все (или почти) число итераций чтобы добиться требуемого значения ошибки и как результат процент ошибки, соответствующий (71,2%)

Процент прспознавания

Таблица 2 – Средний процент распознавания фонем

Для (архитектуры N1=128, N2=64, N33=18, q =0,1) можем получить максимальный процент обучения и можем ожидать желаемую минимальную ошибку.

Отметим также, что так как число нейронов скрытого слоя увеличиваеся и это улучшает требуемый результаты для обучения или распознавания, тогда как с такой же архитектурой, которая нам дает относительно хорошие результаты с байесовским распознаванием, мы имеем одинаковый результат среди обучение градиентом.

В таблице 2 представлены результаты, полученные при распознавания 18 фонем и баейсовскими методами и алгоритмом обратного распространения ошибки. На сотой иттерации, мы получили среднее распознавание равное 57.6% для обратного распостранения ошибки и 62.0% для байесовских методов (128, 64, 18).

Ошибка

Зафиксировано уменьшение ошибки при обучении байесовскими методами по сравнению с ошибкой, полученной при обучении обратным градиентом.

6. Выводы

В этой статье представлены техники обучения нейронных сетей, основанные на принципе методов монте-карло и выборке по значимости. Применяю последнюю в байесовским методам для вычисления интегралов на разных этапах обучения нейронной сети мы получили результаты, которые превосходят результаты обучения с помощью найболее классического алгоритма обратного распостранения ошибки.

Применение этого алгоритма к распознаванию речи четко показывает, что данная техники обучения представляет интересную и многообещающую альтернативу существующим методам. Техника выборки предоставляет лучшее описание распределения вероятностей весов сети чем классические методы.

Мы получили пользу из главного качества выборки по значимости, которым является уменьшение времени вычислений, для улучшения метода монте карло и как следствие минимизания времени обучения нейронной сети.

Можем констатировать также увеличение коэффициента распознавания, а следовательно и уменьшения ошибки классификации фонем, зная что неопределенность весов принята во внимание для корректировки вычисленной вероятности сетью для задачи классификации. Хотя проблема автоматического распознавания речи сложная, мы можем улучшить показатели на 10% перейдя от алгоритмов обратного распостранения ошибки к байесовским методам для обучения нейронной сети, используя выборки по значимости.

Литература

1. D. J. C. MacKay. “Bayesian interpolation”. Neural Computation, 4(3), 415-447, 1992 a.
2. D. J. C. MacKay. “A Practical Bayesian Framework for Backpropagation Networks”. Neural Computation, 4(3), 448-472, 1992 b.
3. R. M. Neal. “Bayesian Training of Backpropagation Networks by the Hybrid Monte Carlo Method”. Technical Report CRG-TR-92-1, Department of Computer Science, University of Toronto, 1992.
4. W. Buntine, A.S “Weigend.Bayesian backpropagation“. Complex Systems, 5, 603-643, 1991.
5. C. M. Bishop. “Neural Networks for Pattern Recognition”. Clarendon Press, Oxford, 1995.
6. JFG de Freitas, M Niranjan, A H Gee, and A Doucet.
7. “Sequential Monte Carlo methods for optimisation of neural network models”. Technical Report CUED/FINFENG/TR 328, Cambridge University Engineering
8. Aki Vehtari et Jouko Lampinen. « Bayesian neural networks with correlating residuals”. In Proc. IJCNN’99, Washington, DC, USA, July 1999.
9. JFG de Freitas. “Robust full bayesian methods for neural network”, Cambridge university , 2000.
10. Philippe Leray et Olivier François, « Etude comparative d’algorithme d’apprentissage et de structure dans les réseaux bayésiens », Laboratoire Perception, Systèmes, Information — FRE CNRS 2645.
11. S.Richardson.Méthodes “bayésiennes en modelisation spatiale”, département of epidemiilogy and public health, imperial college, London.