
Авторы: Кондратьев М.Е.
Источник: Кондратьев М.Е. ОАнализ методов кластеризации новостного потока / М.Е. Кондратьев // Санкт-Петербургский Государственный Университет, 2006.
В работе анализируется ряд алгоритмов кластеризации новостной коллекции и приводится описание экспериментов, направленных на выяснение зависимости эффективности и стабильности кластеризации новостного потока от граничных значений алгоритмов.
С развитием сети Интернет все большую популярность завоевывают сетевые новостные агентства, во многом заменившие традиционные средства информации. Большое количество источников информации, резко возросший объем новостных данных и необходимость их быстрой обработки вызвали потребность в создании систем автоматизированного анализа новостного потока. Наиболее известной конференцией, посвященной методам автоматизированной обработки новостных данных, является Topic Detection and Tracking (TDT), где выделяются следующие направления исследований: разбиение потока на сюжеты, идентификация новых событий, определение связей между новостными историями, отслеживание интересующей пользователя информации.
Задачи, связанные с обработкой новостного потока, имеют специфичные особенности, определяемые природой новостных данных. Новостные сообщения являются откликами на события реального мира и поэтому кроме текстового наполнения сюжет объединяют причинно-следственные, временные и прочие факторы. Эта особенность используется некоторыми системами, которые учитывают информацию о времени публикации сообщений [8] и основных действующих лицах [ 3] при решении задач обработки новостей. Тот факт, что новостные сообщения становятся доступны пользователю в виде потока данных, делает невозможным разбиение уже сформированных сюжетов. Отметим так же, что число сюжетов заранее неизвестно и потенциально неограниченно.
Одной из важнейших задач автоматизированной обработки новостного потока является разбиение новостных сообщений на сюжеты (кластеризация новостного потока). Вследствие потоковой природы новостных данных в значительной части работ используется алгоритм инкрементальной кластеризации:
– выбирается мера близости нового сообщения и кластера;
– для каждого нового сообщения выбирается кластер, наиболее близкий к сообщению;
– в случае, если значение меры близости превышает некоторое пороговое значение, сообщение добавляется в уже существующий кластер;
– в случае если значение меры близости не превысило пороговое значение, создается новый кластер на основе нового сообщения.
Для оптимизации качества кластеризации могут использоваться различные вариации приведенного алгоритма. Так, например, Яндекс.Новости, выполняют кластеризацию в несколько проходов с целью объединения атомарных кластеров.
За время проведения конференции TDT (с 1998 по 2004 год) было предложено множество достаточно эффективных алгоритмов решения задачи кластеризации новостного потока, однако вопрос о стабильности предложенных методов остается открытым. Как видно из описания алгоритма, эффективность работы системы кластеризации в первую очередь зависит от выбранной меры и правильного определения граничного значения. Несмотря на то, что те или иные граничные значения используется практически во всех работах, нам не известно исследований, направленных на выяснение вопроса стабильности порогового значения на данных коллекции. Для получения повторяемого результата необходимо ответить на следующие вопросы: как ведет себя граничное значение для различных мер? Насколько стабильно найденное граничное значение? Какие меры предпочтительнее в терминах эффективности и стабильности граничных значений?
Целями данного исследования был поиск оптимальных граничных значений для различных мер близости, выяснение стабильности найденного значения и сравнение эффективности алгоритмов.
В современных работах описывается множество различных мер и базирующихся на них алгоритмов кластеризации новостного потока. Для наших исследований были отобраны следующие меры:
Наиболее простой мерой близости двух документов представляется мера совпадения множеств термов документов, известная так же как мера Джаккарда (Jaccard) [9]. Эта мера определяется как

где A и B – множества термов, входящих в текстовые документы. Из формулы видно, что мера принимает значения от 0 до 1 и достигает максимума при полном совпадении двух множеств. Данная мера чрезвычайно проста, однако содержит ряд недостатков. Выделим два из них. Во-первых, мера не учитывает разницу в размере сравниваемых документов, а во-вторых, при ее вычислении не используется информация о частоте употребления термов, составляющих документы.
Нами было рассмотрено несколько алгоритмов, использующих эту меру: Story Similarity, Story Minimal Similarity, Subject Similarity, Named Entities Similarity, а также аналогичная мера Sub Similarity.
Алгоритм Story Similarity вычисляет расстояние от нового документа до кластера как максимальное значение меры Джаккарда, вычисленное для нового сообщения и документов кластера. Story Minimal Similarity так же использует меру Джаккарда, однако в качестве расстояния до кластера принимается минимальное значение меры, вычисленное для нового новостного сообщения и документов кластера. Алгоритм Subject Similarity аналогичен Story Similarity, но при вычислении меры использует только информацию заголовков.
В задачах, связанных с обработкой новостного потока и в первую очередь в задачах идентификации новых событий часто применяются методы, анализирующие множества именованных сущностей, присутствующих в документе [3]. Для упрощения задачи в нашем алгоритме Named Entities Similarity идентификаторами считались любые термы, начинающиеся с заглавной буквы. В качестве меры близости множеств именованных сущностей использовалась мера Джаккарда.
Для новостных сюжетов характерно, что в ходе развития событий более ранние сообщения агрегируются более поздними. Для проверки этой гипотезы была введена мера Sub Similarity, определяющаяся как отношение мощности пересечения множеств термов к мощности наименьшего множества [2]:

Описанная мера показывает, насколько одно новостное сообщение включается в другое. Расстояние от документа до кластера в алгоритме Substory Similarity определяется как максимальное значение меры, вычисленное для нового сообщения и документов кластера.
В основе этого алгоритма лежит идея о голосующих классификаторах, успешно показавшая себя в некоторых работах [5], связанных с кластеризацией новостного потока. Мы предполагаем, что использование комбинации классификаторов, каждый из которых вносит вклад в принятие решения, позволит достичь лучших результатов, чем применение классификаторов по одному. В нашем исследовании в качестве голосующих классификаторов использовались вышеперечисленные алгоритмы. Вклад каждого из классификаторов оценивался как

где MeasureVal – значение меры схожести i-го алгоритма, ThresholdVal – граничное значение, используемое в алгоритме.
Решение о принадлежности к одному из существующих кластеров принималось на основе анализа суммы значений VoteVal. Новое сообщение относилось к кластеру, для документа которого суммарное значение VoteVal было максимально и превышало заранее установленное граничное значение.
Различные вариации мер, основывающихся на векторном представлении документов и tf*idf взвешивании термов чрезвычайно популярны в задачах новостной кластеризации ( [8], etc.) В наших экспериментах использовалась широко распространенная мера схожести документов, определяющаяся как косинус угла между векторами, представляющими документы:
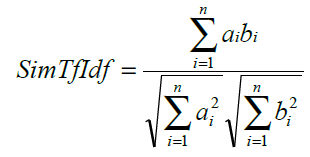
где ai и bi – компоненты векторов документов A и B, n – размерность векторов. Для построения векторов и вычисления весов термов использовался вариант формулы tf*idf:
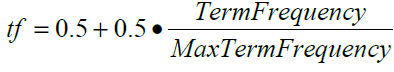
где TermFrequency – частота терма в документе, а MaxTermFrequency – максимальная частота термов в документе

, где N – общее число документов в коллекции, а df – количство документов, в которых встречается терм.
Как видно, применение такой меры близости документов позволяет учесть частоты термов документов, однако требует использования статистических данных о частоте термов во всей коллекции. В условиях нашей задачи это требование никогда не может быть выполнено полностью, так как размер коллекции и множество составляющих ее документов заранее неизвестны, однако может аппроксимироваться на основе уже полученных знаний.
Различные исследования, анализирующие методы классификации текстовых документов признают метод опорных векторов (SVM) [6] одним из наиболее эффективных. В нашем исследовании мы применили SVM классификатор для задачи кластеризации новостного потока. В качестве вектора пространства признаков использовался вектор, элементами которого являются значения метрик, полученных при вычислении по алгоритмам Story Similarity, Subject Similarity, Named Entities Similarity, Substory Similarity.
Для обучения классификатора использовалась размеченная новостная коллекция. Обучение выполнялось следующим образом: для каждого нового документа из существующих кластеров последовательно выбирались сообщения, относительно которых строился вектор признаков. В случае если новое новостное сообщение и существующее сообщение должны, согласно разметке, принадлежать различным сюжетам, вектор относился к множеству отрицательных примеров. В случае, когда новое сообщение и существующий документ принадлежат одному кластеру, вектор помечался как положительный пример, из потока выбирался следующий документ и процесс начинался сначала. Выполненное таким образом обучение позволяет свести задачу кластеризации к классификации на два множества. Описанный алгоритм основывается на гипотезе, что вектор признаков содержит достаточно информации для принятия решения о принадлежности (или непринадлежности) истории кластеру.
Алгоритм кластеризации с использованием SVM выглядит следующим образом:
Результат работы приведенного алгоритма сильно зависит от последовательности перебора существующих кластеров и историй в них, так как решение принимается на основе первого положительного примера. В целях устранения этого недостатка нами использовалась модифицированная версия алгоритма, где помимо решения классификатора во внимание принимались значения метрик из пространства признаков. Использование значений метрик позволяет определить кластер, наиболее близкий рассматриваемому сообщению.
Одной из особенностей задачи кластеризации новостного потока является тот факт, что количество кластеров заранее неизвестно и неограниченно. Эта особенность делает неэффективной широко распространенную оценку качества кластеризации, основанную на понятии энтропии. Из определения метрики следует, что она будет достигать наилучшего значения, когда размер кластеров будет наименьшим. Очевидно, что наилучшее значение при таком методе оценки будет получено при использовании классификатора, создающего новый кластер для каждого нового сообщения потока, что не соответствует действительности.
Все эксперименты проводились на основе новостной коллекции семинара РОМИП 2005. Для сообщений потока выполнялся стемминг и из текста исключались стоп-слова.
В силу временных ограничений в рамках РОМИП кластеризация данных асессорами не производилась. Для анализа и настройки алгоритмов в нашем исследовании была выполнена ручная разметка двух подмножеств коллекции, состоящих из 500 сообщений каждый (коллекция A и коллекция B). Оценка производилась двумя асессорами, причем первый асессор оценивал коллекцию A, а второй - коллекцию B. В результате выполненной вручную кластеризации в коллекции A были выделены 261, а в коллекции B 268 новостных сюжетов.
Учитывая тот факт, что количество кластеров, выделенных вручную, достаточно велико и среди них значительную часть составляют атомарные кластеры, в качестве базового алгоритма был выбран алгоритм кластеризации, создающий новый кластер для каждого нового сообщения новостного потока. Для базового классификатора были получены следующие значения метрик на первом подмножестве: F=0.83, Fr=0.64.
Одной из задач данного исследования было определить оптимальные граничные значения для исследуемых алгоритмов и выяснить устойчивость найденных значений. Исследование алгоритмов проводилось в два этапа. На первом этапе выполнялась настройка граничного значения на первом размеченном подмножестве новостной коллекции.
При настройке алгоритмов выбирались граничные значения в определенном диапазоне с малым шагом. Диапазон выбирался исходя из теоретических ограничений (0..1 для всех алгоритмов кроме голосующей кластеризации). Для каждого из выбранных значений выполнялась кластеризация, результаты которой оценивались с помощью обеих метрик, F и Fr. Рассмотрим результаты экспериментов более подробно.
Алгоритмы, использующие меру Джаккарда Данная мера использовалась в алгоритмах оценки максимальной и минимальной схожести документов, максимальной схожести заголовков и множеств идентификаторов.
Построение кластера на основе поиска максимально похожей истории дает несколько лучшие результаты (максимальные значения метрик F=0.93, Fr=0.8) по сравнению с методом, в котором новое сообщение относится к кластеру, в котором минимальное значение меры схожести максимально (максимальные значения метрик F=0.92, Fr=0.77). Полученные результаты подтверждают гипотезу, согласно которой кластер новостных сообщений должен рассматриваться как развивающийся сюжет, и признаком принадлежности кластеру является близость нового документа одному из документов кластера, а не его центру. В то же время, разница в значениях метрик F и Fr составляет 1 и 3 процента соответственно, что не позволяет говорить о принципиальном преимуществе одного из подходов.
Метод кластеризации, основывающийся на сравнении заголовков, показал достаточно низкие результаты (максимальные значения метрик F=0.88, Fr=0.69). Это позволяет говорить о недостаточности данных, содержащихся в заголовках для принятия решения о принадлежности сюжету.
Метод кластеризации, использующий только идентификаторы, показал наихудшие результаты среди всех рассматривающихся алгоритмов (максимальные значения метрик, F=0.86, Fr=0.69), незначительно превышающие результаты базового классификатора (F=0.83, Fr=0.64). Несмотря на то, что данный алгоритм в некоторой степени не оправдал возложенных на него надежд, может быть интересно его использование в комбинации с другими методами кластеризации.
Алгоритм, использующий меру SubSim, показал достаточно хорошие результаты, совпадающие с наилучшими результатами описанных выше алгоритмов. Наилучшие значения мер: F=0.93, Fr=0.8
Голосующая кластеризация. Использование комбинации алгоритмов позволило несколько улучшить результат (максимальные значения метрик F=0.93, Fr=0.82) по сравнению со значениями, полученными индивидуальными алгоритмами, участвующими в голосовании.
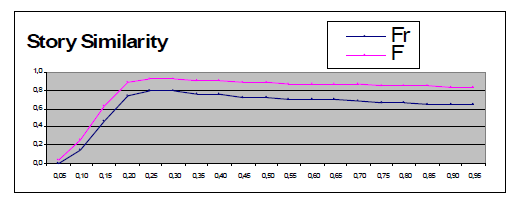
Если сравнить графики зависимости качества классификации от граничного значения, можно заметить, что все меры, основанные на мере Джаккарда, имеют ярко выраженный промежуток роста, а затем медленно убывают. График голосующего классификатора по форме значительно отличается от зависимостей, полученных для других алгоритмов, в нем нет ярко выраженных промежутков роста и убывания функции. Этот факт объясняется тем, что, комбинируя алгоритмы, мы компенсируем ошибки одних из них правильными решениями других.
Мера Tf * Idf. Использование Tf*Idf меры позволило получить наилучший результат кластеризации (F=0.96, Fr=0.88). Оптимальное пороговое значение составило 0.2. Стоит, однако, заметить, что применение такого метода кластеризации требует накопленной статистической информации о частотах термов в документах новостного потока. В данном эксперименте использовалась статистика, полученная на первом оцененном подмножестве новостной коллекции (словарь составил порядка 11000 слов), к которой затем и применялся алгоритм кластеризации. Такая оценка не совсем корректна, так как в данном случае алгоритм использовал ‘идеальную’ статистику.
Для получения более корректного результата нами был проведен дополнительный эксперимент (см. график), в ходе которого для сбора статистики использовалось порядка 4000 новостных сюжетов (словарь составил 43000 слов). Данная коллекция не включала оцененное подмножество. Результаты эксперимента показали, что оптимальное граничное значение сместилось к отметке 0.25-0.3, значения метрик Fr и F опустились до 0.84 и 0.95 соответственно.
На первом этапе экспериментов основной задачей для SVM кластеризации было обучение классификатора для дальнейшей оценки его эффективности в последующих экспериментах. В результате обучения было получено более 65000 обучающих векторов, большая часть которых относится к множеству отрицательных примеров, то есть описывают случай, когда история не должна быть причислена к рассматриваемому кластеру. В качестве первичной проверки SVM-алгоритма кластеризация была выполнена на обучающем множестве. Полученные результаты превзошли результаты всех прочих алгоритмов (F=0,95, Fr=0.85) , что позволило признать метод перспективным для дальнейшего анализа.
Подводя итог первого этапа экспериментов по настройке алгоритмов, отметим, что из всех алгоритмов наилучшие значения метрик были достигнуты на алгоритмах Story Similarity, Substory Similarity, голосующей кластеризации и Tf*Idf.
Основными задачами второго этапа экспериментов были проверка стабильности работы исследованных алгоритмов на другом оцененном подмножестве новостной коллекции и сравнение их эффективности. Помимо этого на втором этапе экспериментов проводилась проверка эффективности предложенного нами метода кластеризации на основе SVM классификатора.
Полученные результаты работы базового классификатора для коллекции B: F = 0.83, Fr = 0.63.
Для экспериментов нами были отобраны наиболее перспективные алгоритмы, для которых были поставлены опыты, аналогичные экспериментам первого этапа, но с использованием коллекции B новостных сообщений.
В таблице приведены оптимальные граничные значения, полученные на втором этапе экспериментов и соответствующие им значения метрик качества кластеризации. Для удобства сравнения в таблице так же приводятся граничные значения, оптимальные для первой оцененной коллекции.
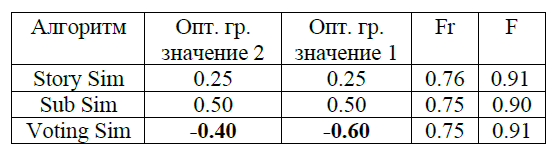
Из приведенных результатов экспериментов видно, что на рассмотренных алгоритмах, за исключением голосующей кластеризации, оптимальное граничное значение достигается в той же точке, что и в экспериментах на первой оцененной коллекции. Дополнительные эксперименты с использованием алгоритмов Subject Similarity и Named Entities Similarity показали, что и в этом случае наблюдается стабильность найденных граничных значений.
Расхождение в оптимальных граничных значениях для алгоритма голосующей кластеризации можно считать условным, так как значения метрик колеблются вокруг среднего значения и максимальная разница по мере Fr, например, достигает всего лишь 5 процентов.
Tf*Idf Similarity На втором этапе экспериментов Tf*Idf алгоритм применялся 2 раза, в первый раз с использованием статистики, накопленной только на первом оцененном подмножестве коллекции. Результаты алгоритма оказались неожиданно высоки для такого малого объема статистических данных: максимальное значение метрики Fr=0.78, F=0.92. При этом оптимальное граничное значение осталось неизменным по сравнению с опытами первого этапа - 0.3. Видно, что эти результаты превысили результаты работы алгоритмов, не учитывающих частотное распределение термов.
Для сравнения был поставлен второй эксперимент с использованием статистики, полученной на подмножестве коллекции из примерно 4000 документов. Несмотря на больший объем данных, результаты практически не изменились. Лучшее качество кластеризации по-прежнему достигается на отметке 0.3, значения мер Fr и F достигают 0.79 и 0.92 соответственно:
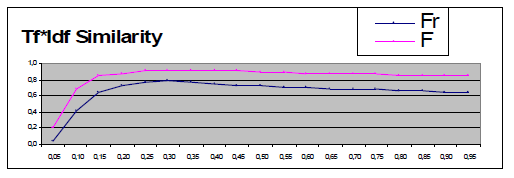
Полученные данные позволяют сделать вывод об относительной стабильности работы рассматриваемых алгоритмов и найденных граничных значений. Важно так же отметить, что вид зависимости эффективности кластеризации от выбранного граничного значения сохраняется на втором подмножестве коллекции.
Несмотря на то, что эксперименты показали относительную стабильность найденных оптимальных параметров алгоритмов, нас интересовал вопрос субъективности оценки коллекции асессором. Для выяснения этого факта Коллекция B была повторно размечена тем же асессором, который оценивал Коллекцию A. Сравнение двух вариантов разметки коллекции B показало, что лишь около 80 процентов кластеров совпадает. Очевидно, что такое сильное расхождение в оценке не могло не сказаться на значениях метрик качества классификации. В связи с полученными данными можно сделать вывод, что результаты работы различных систем существенно субъективны и могут значительно варьироваться в зависимости от конкретного асессора.
Одной из задач второго этапа экспериментов была проверка эффективности применения SVM классификатора для решения задачи кластеризации новостного потока. SVM классификатор, обученный на коллекции A, показал средние результаты при кластеризации коллекции B: Fr=0.76, F=0.90.
Тот факт, что обучение даже на небольшой коллекции (500 документов) позволило достичь достаточно хорошего результата на независимом множестве документов, позволяет расценивать SVM метод как перспективный алгоритм, требующий более подробного изучения. В дальнейших исследованиях мы планируем изучить влияние расширения пространства признаков и конкретного ядра алгоритма на эффективность кластеризации.
В данной работе был рассмотрен ряд алгоритмов кластеризации новостного потока и определены оптимальные параметры данных алгоритмов с использованием размеченного подмножества новостной коллекции РОМИП 2005. Наилучшие результаты по итогам двух серий экспериментов были показаны алгоритмом Tf*Idf.
Проведенные исследования поведения различных алгоритмов подтвердили относительную стабильность оптимального граничного значения при инкрементальной кластеризации. Предложенный нами метод кластеризации на основе классификатора SVM продемонстрировал достаточно хорошие результаты, однако требует дополнительных исследований и оптимизации.