Высокопроизводительная алгоритмическая технология для 3D графики
Автор: Горшков А.С. кандидат физико-математических наук,
г. Москва
Источник: International Conference Graphicon 1999, Moscow, Russia, http://www.graphicon.ru/.
Аннотация
Разработан принципиально новый метод и система алгоритмов для построения 3D моделей, ориентированных на широкий круг задач, где применяется 3D графика (САПР, томография, 3D игры). Отличительными свойствами нового механизма, обеспечивающими принципиальные преимущества перед известными и наиболее распространенными подходами на основе триангуляции иz-буфера, являются полноценно аналитический подход к формированию структур данных, в частности исчерпывающее использование линейных математических методов, а также специальное обобщение известных растровых алгоритмов 2D графики. Благодаря этому достигнута возможность полностью отказаться от примененияz-буфера, а также реализовывать поверхность 3D моделей не только из треугольников, но и полигонов (многоугольников) общего вида(полиангуляция). В результате достигается значительно большее разнообразие моделируемых форм при значительно меньшем числе элементов внешней поверхности(количество полигонов может быть меньше на один-два порядка относительно необходимого числа треугольников) и, соответственно, очень высокая производительность. При необходимости достижения максимальной скорости обработки на основе аппаратной поддержки(3D акселератора) такой акселератор может быть реализован наиболее компактно благодаря очень высокой степени унификации всех алгоритмических решений, что обеспечит его невысокую стоимость.
Ключевые слова: : полигон, полиэдр, полиангуляция, пиксельный растр, х-буфер, z-буфер, xz-буфер, компрессия.
1. Введение
Разработанная автором новая методика построения алгоритмов 3D обработки была предложена с целью решения следующих важнейших задач обработки и отображения трехмерных данных.
- Полнооб'емное3D моделирование, допускающее возможность исследования внутренних структур об'ектов. Этим подразумевается, что об'ект может описан не только внешней поверхностью, но и 3D массивом внутренних данных, над которыми можно выполнять операции разрезов, сечений, выделения поверхностей.
- Возможность создавать поверхности наиболее
сложных форм из наименьшего количества
элементов. Построение внешних поверхностей
об'ектов выполняется на основе нового
оригинального метода линейной полигональной обработки – полиангуляции (заключающийся в
применении полигонов любого порядка и различных
типов- как выпуклых, так и невыпуклых, а также
возможно и с самопересечением). Этот метод
обеспечивает значительно большее разнообразие и
более высокое качество форм поверхностей в
сравнении с ширoко распространенным методом
триангуляции, а также позволяет исключить
необходимость использованияz – буфера.
С самого начала освоения и развития данной практической отрасли основной вес среди методов построения об'емных проекций заняла поточечная сортировка с помощью двумерной таблицы глубин, известной как «z-буфер». Данный метод оказался привлекательно прост именно в смысле отсутствия каких-либо вычислений вообще путем простого сравнения значений глубины. Это позволило широко развернуть разработку большого количества программ и баз данных для всех прикладных ситуаций. Однако очень быстро проявились и принципиальные недостатки такого подхода.
В первую очередь, это очень медленная обработка даже данных невысокой сложности. Попытки преодолеть этот недостаток вылились в конце концов в развитие аппаратных решений для обеспечения 3D графики, известных как «3D-акселераторы». На данный момент возможности развития в этом направлении фактически полностью исчерпаны и ограничиваются только уровнем развития микроэлектронных технологий, которые, видимо, также вышли на физический предел. Отсюда неизбежно должен быть вновь проявлен интерес к развитию математического алгоритмического аппарата, который позволил бы более полноценно использовать аппаратные возможности современных компьютеров.
Другое обстоятельство связано с невозможностью в общем случае построить и выделить четкие границы пересекающихся элементов модели. И в третьих, применение произвольных треугольников для моделирования непрерывных поверхностей также приводит к существенным затруднениям:- для аппроксимации достаточно сложных поверхностей требуется очень большое количество узловых вершин и связывающих их треугольников, что приходится выполнять разработчику вручную с помощью специальной программы-редактора, либо применять заготовки моделей(как например, в пакете 3D Studio-Max), что ограничивает выбор пользователя;
- затруднительно или вообще невозможно получить изображение поперечного сечения триангулированной модели произвольной плоскостью;
- невозможность в общем случае выполнить каким-либо образом сортировку треугольников, даже составляющих непрерывную поверхность, по удаленности от наблюдателя, что заставляет разработчика триангуляционной модели применять методz-буфера.
С учетом этих ограничений автором также было обращено внимание на недостаточное использование хорошо известных формул аналитической геометрии и векторного анализа в разработке алгоритмов для3D моделирования. Одновременно сделан переход к интегрированной обработке данных, под чем подразумевается переход от ввода и редактирования отдельных вершин к обработке об'емных областей, генерация которых управляется плоскими сечениями, необходимый список вершин соответственно формируется автоматически.
Использование z-буфера может наряду с этим быть сохранено в случае включения в моделирование дополнительных геометрических форм, например, тел 2-го (шар, цилиндр, конус) или 4-го порядка(тор) для построения более сложных и качественных моделей. - Телевизионный принцип построения 2D проекции
об'емной сцены, обеспечивающий наиболее высокую
скорость формирования конечного изображения. Под
телевизионным принципом построения пиксельного
растра понимается последовательное заполнения
скан-линий(строк) изображения, выводимого на
экран монитора компьютера. Это свойство отвечает
существенно одномерной природе данных,
находящихся в памяти компьютера, а также
последовательному типу их передачи по каналам
связи.
В целом разработанная система отличается наибольшим универсализмом фунций при предельной унифицированности.
2. АЛГОРИТМИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
Перечисленные выше новые возможности обеспечиваются на основе следующих новых наиболее важных алгоритмических решений:
- обобщение алгоритмов растровой графики Брезенхэма, на основе чего получены наиболее короткие и быстрые алгоритмы построения отрезков прямых, полигональных областей (включая как закрашивание различными методами, так и наложение 2D текстур, либо 3D сечений), трассирование лучей по трехмерному массиву;
- оригинальный векторно-аналитический метод разбиения пространства на выпуклые многогранники с быстрой сортировкой по глубине на основе бинарного дерева, благодаря чемудостигается гибкое построение3D моделей, внешняя поверхность которых аппроксимируется набором многоугольников произвольного порядка, а также их редактирование(проведение сечений и удаление отдельных элементов) и оперативная манипуляция в реальном времени (перемещение, вращение и масштабирование от кнопок клавиатуры или манипулятора «мышь»).
3. МЕТОД СОГЛАСОВАННЫХ ЦИКЛОВ
Метод согласованных циклов представляет собой об'единение нескольких программных циклов различной длины, которые должны быть выполнены синхронно, т.е. более короткие растянуты до наиболее длинного, в один общий цикл специального вида. Частным случаем применения такого метода является хорошо известный алгоритм Брезенхэма построения отрезков прямых на дискретном изображении, на основе изучения и обобщения которого и был получен новый метод.
Основной смысл применения данного подхода состоит в избежании использования операции деления при пропорциональных расчетах. Это позволяет реализовывать наиболее быстро операции растяжения-сжатия масивов данных, что особенно актуально для задач проективной графики. Всякая строка изображения2D проекции об'емной сцены состоит из интервалов, образованных отрезками2D текстур либо3D трасс. Каждый такой отрезок задается на исходных данных соответственно двумя или тремя координатами. Тогда при необходимости линейно спроектировать такой отрезок на интервал строки изображения заданной длины возникает задача пересчета координат, которая решается в форме известных пропорций, т.е. операций, содержащих умножение и деление. Устранение необходимости этих операций, заметно ограничивающих скорость обработки, достигается на основе операции приведения по модулю.
Другим достоинством данного метода является гарантированное непересечение промежуточными отсчетами границ как входных массивов данных, так и конечного изображения, что исключает необходимость их проверки, в силу того, что начало и конец каждого отдельного цикла обхода данных изначально заданы и тем самым жестко фиксированы. Это обстоятельство заметно ограничивает скорость часто применяемого подхода на основе погонного вычисления координат путем постоянного приращения, когда происходит одновременное накопление вычислительных ошибок.
Метод имеет наиболее простую и быструю реализацию для случаев вычисления только адресов данных(если собственно координаты не требуются). В частности, алгоритм построения отрезка прямой по сравнению с исходным вариантом, который обычно приводится в литературе по программированию графики, резко сократился по размеру кода и по времени реализации.
Важнейшие случаи применения данного метода следующие:
- построение отрезка прямой (2 цикла в одном);
- построчная развертка 2D текстуры (3 цикла в одном);
- построчные проекции 3D трасс (4 цикла в одном);
- трассирование луча в 3D массиве (3 цикла в одном).
4. ПОСТРОЕНИЕ ОБ'ЕМНЫХ МОДЕЛЕЙ
В основу нового подхода к построению моделей об'емных тел положена простая идея разбиения пространства на блоки путем разрезов его секущими плоскостями. В качестве исходного элемента применяется тело наиболее простой формы- параллелепипед, последовательное сечение которого образует набор выпуклых полиэдров (многогранников), т.е. тел, поверхность которых образована выпуклыми полигонами соответствующего порядка, который, как правило, выше третьего.
Такое разбиение обладает следующим важным свойством: каждый из полученных полиэдров находится по ту или иную сторону относительно каждой их использованных для сечения плоскостей, что позволяет сформировать двоичный код, однозначно задающий положение каждого из них относительно остальных.
Лишние полиэдры далее отбрасываются, и в итоге образуется тело требуемой формы, поверхность которого аппроксимирована выпуклыми полигонами (рис.1). Очевидно, что всякое выпуклое тело, например, кристалл алмаза, будет представлено одним полиэдром, большинство же реальных тел невыпуклые, и это обуславливает необходимость применения для их моделирования данного аппарата.
В силу выпуклости каждого из элементов этого общего набора плоская проекция полученного тела строится как последовательность проекций примыкающих к внешней поверхности полиэдров в порядке, определяемым их кодом в бинарном дереве. Код положения каждого такого полиэдра модифицируется с учетом конкретного ракурса проекции с помощью маски ИСКЛ-ИЛИ, биты которой определяют видимость-невидимость лицевой стороны каждой секущей плоскости. Также в силу выпуклости каждый полиэдр на проекции оказывается представлен только его видимыми гранями, лежащих на внешней поверхности модели. В итоге обеспечивается очень простая и быстрая сортировка по глубине, выявляющая необходимость отображения те или иных полигонов в простой последовательности.
Каждый из полученных полиэдров снова может рассматриваться как новое подпространство, к которому может быть применена та же технология обработки- сечение новыми плоскостями, построение нового бинарного дерева относительных положений и устранение ненужных элементов.
Существенным преимуществом представленной технологии является возможность легко получать разрезы и сечения об'ектов, так как это лишь одна из функций, используемых для их построения. Сечение при этом представляет собой набор несмежных полигонов(в общем случае и невыпуклых), лежащих в одной общей плоскости (рис.2).
С математической точки зрения данный алгоритмический аппарат является предельно простым, фактически все процедуры построены на единственной формуле пересечения отрезка прямой и плоскости. Основная сложность реализации связана с генерацией эффективных структур данных.
Существуют также более простые частные случаи этого метода. Например, для построения рельефа местности или об'емных карт сначала выполняется разбиение и поэлементое двоичное кодирование на плоскости, а не в пространстве, после чего на каждом полученном выпуклом полигоне этой плоскости строится выпуклый полиэдр указанным выше способом.
5. МЕТОД ТЕЛЕВИЗИОННОЙ РАЗВЕРТКИ ПРОЕКЦИЙ
Для достижения наивысшей производительности и поддержания очень высокой скорости обработки данных (быстрая генерация новых полиэдров при сечении и быстрая сортировка при изменении ракурса проекции) разработан также метод наиболее скоростного построения растра проекции. Существо метода заключается в построении промежуточных структур данных, обеспечивающих последовательное заполнение изображения строка за строкой, интервал за интервалом. Под интервалами понимаются непрерывные последовательности пикселов и соответствующих им ячеек памяти, которые должны заполняться по одному общему алгоритму.
Существуют интервалы следующих типов:
- одноцветные области;
- однострочный отрезок проекции 2D текстуры;
- однострочный отрезок проекции трассы 3D массива.
После получения последовательности отображаемых на экран полигонов, отсортированных и ранжированных в порядке уменьшения глубины относительно экрана, производится отсечение перекрывающихся элементов и заполняется массив специальных структур данных, который и будет определять формирование строк на конечном этапе. Такие промежуточные структуры представляют собой по существу буфер границ областей, который строится, в силу того, что эти области полигональные, также по методу согласованных циклов.
Данный метод также может быть распространен и на общий случай обычной триангуляции, когда неизбежно приходится применять z-буфер. Буфер границ областей, который можно также условно назвать «x-буфером», так как он обеспечивает формирование строчных границ отдельных интервалов, в этом случае выступает в роли «xz-буфера», потому что может также поддерживать обработку пересекающихся по глубине строчных отрезков. В любом случае достигается существенное преимущество по скорости обработки, так как сортировка по глубине выполняется не над отдельными точками, а над целыми областями, затем строчными интервалами отсортированных областей.
Способ промежуточного представления данных для обеспечения такого метода развертки проекций сходен с известными методами компресии(сжатия) 2D изображений путем погонного уплотения(RLE – run-length encoding). Тем самым он также может рассматриваться как их расширение на область 3D форматов данных и послужить в дальнейшем основой для разработки универсального стандарта.
6. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ
Представленные алгоритмы реализованы в форме функций на языкеBorland C++ (пакеты версий4.52 и 5.02) иTurbo Assembler 5.0 и собраны в предельно компактную библиотеку процедур(общий об'ем текста составляет лишь несколько десятков килобайт). Основные отличительные свойства этой библиотеки:
- использование небольшого числа(около одного десятка) классов для описания лишь наиболее важных геометрических об'ектов(2D и 3D точки, полигональные области, буфер изображения в памяти);
- широкое использование операторов для сокращения текстов программ(например, скалярное произведение векторов обозначается как обычное умножение «*»);
- реализация наиболее базовых и часто повторяющихся операций(таких как построение линий и областей, скалярное и векторное произведение и т.д.) на ассемблере;
- расширенный класс буфера изображения по сравнению со стандартным классомTDib (BC++ 5.02).
7. ЗАКЛЮЧЕНИЕ
Представленный в настоящем докладе новый алгоритмический аппарат и технология моделирования и обработки 3D об'ектов составляют новый шаг в развитии методов 3D моделирования и графики. Данная методика по существу дает исчерпывающие возможности в использовании полноценно математических методов работы с 3D об'ектами на классе линейного приближения.
Разработанный алгоритмический аппарат максимизирует производительность за счет специальной ускоренной обработки об'ектов линейного типа(построенных на основе отрезков прямых и полигональных участков плоскостей).
Расширены возможности по моделированию об'ектов более разнообразных форм благодаря переходу от триангуляционной аппроксимации их поверхностей к полиангуляционной. Способ генерации полигональных поверхностей при этом также обеспечивает интегрированную обработку, при которой ввод и генерация данных производятся на основе задания ключевых параметров, а не самих конкретных значений, что резко повышает производительность разработчика. Достигнута возможность отказа от поточечной сортировки элементов3D сцены по их удаленности на основеz-буфера. Применение z-буфера при этом не исключается совсем, но отодвигается либо на случаи нелинейной обработки (использование таких форм как шар, цилиндр, конус, тор- рис.3), либо при неэффективности применения детальных аналитических расчетов, когда их об'ем сопоставим по сложности с поточечной проверкой с помощью z-буфера. Существенно усовершенствованы методы растровой графики. Реализованные в данной технологии структуры промежуточных данных имеют свойства сжатого представления сложной информации и могут быть использованы для расширения методов компрессии изображений.
ОБ АВТОРЕ
Горшков Алексей Станиславович, кандидат физико-математических наук. Закончил Московский физико-технический институт. Научно-практическая специализация- прикладная математика и цифровая обработка информации. Опубликовано около40 научных статей в центральных научных журналах включая «Доклады Академии наук СССР», а также монография «Цифровая обработка сигналов: атомарные функции и теория чисел» (М.: Машиностроение, 1994, 224 с.). Выступал с докладами на ГРАФИКОН в1992, 1995, 1996 гг.
E-mail: f2813@msk.sitek.net.

Рисунок 1 – Модель инструмента, построенная с помощью новой технологии из выпуклых полиэдров
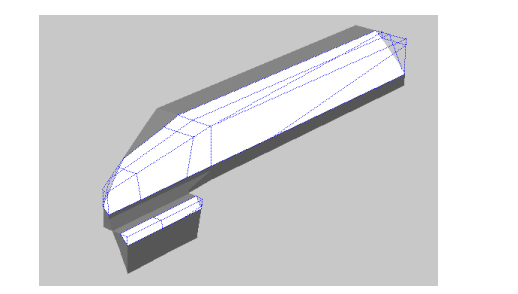
Рисунок 2 – Разрез модели

Рисунок 3 – Шахматы. Все фигуры построены только из шаров, цилиндров и конусов