Теория распознавания образов – раздел кибернетики, развивающий теоретические основы и методы классификации и идентификации предметов, явлений, процессов и тому подобных объектов, которые характеризуются конечным набором некоторых свойств, признаков. Создание искусственных систем распознавания образов остается сложной теоретической и технической проблемой. Необходимость в таком распознавании возникает в самых разных областях. В данном исследовании была поставлена цель – создать алгоритм распознавания образца на изображении формата JPEG и реализовать его на языке программирования высокого уровня. Для достижения данной цели необходимо было овладеть навыками чтения изображения данного формата и найти способ установления зависимости между образцом и участком изображения. Для реализации поставленных задач был выбран язык программирования Delphi. Изображение по сути это массив пикселей. Когда мы открываем изображение в Delphi, каждый пиксель представляется нам неким четырех байтным числом такого формата (рис.1).
Числа BB, GG, RR составляют интенсивность того или иного цвета в пикселе, т.е. величина каждой составляющей BB, GG, BB, от 0 до 255, определяет цвет пикселя. Для количественной оценки яркости пикселя я в своей работе беру их сумму, что является вынужденным упрощением. Формат JPEG имеет изменчивую структуру, зависящую от степени компрессии. Найти некую часть изображения, образец, можно с помощью корреляционного анализа. Рассмотри способ оценки связи между двумя случайными переменными X и Y . Относительно X и Y получены выборки размерности т, обозначим их в виде векторов:
Пусть переменные X и Y имеют нормальный закон распределения. Пользуясь статистическими методами обработки информации получим несмещенные
оценки математического ожидания то есть выборочные средние
. Рассмотрим выборочный линейный парный коэффициент корреляции Карла Пирсона:
По мере приближения этого коэффициента к единице мы можем судить о зависимости между двумя случайными векторами.
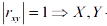– линейно зависимы;
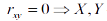– линейно независимы.
Близость коэффициента корреляции к 1 по абсолютной величине говорит о достаточно тесной линейной связи. То есть, с помощью коэффициента корреляции
К. Пирсона можно выявить схожесть между двумя изображениями. В нашем случае 
– значения пикселей образца и изображения. Так мы проходим
по всем пикселям изображения с левого верхнего угла и считаем коэффициенты корреляции при каждой точке. Если 
,
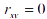то эти переменными считаются некоррелированными, т.е. установить наличие функциональной связи не предоставляется возможным. Утверждать их независимость нельзя.
В ходе исследования была выдвинута гипотеза, что значения коэффициента корреляции равномерно убывают от места нахождения координат образца. Для проверки
этой гипотезы, при поиске образца, создавалась еще одна форма, размером совпадающая с картинкой и на ней закрашивались пиксели в соответствии со значением
коэффициента корреляции текущего образца и картинки. По мере его изменения от 0 до 1 соответствующим координатам присваивался свой оттенок:
пикселю, в котором коэффициент корреляции максимальный присваивался самый светлый оттенок, по мере его уменьшения, цвет становился более темным.
Пример графического отображения коэффициента корреляции показан на рисунках 3 и 4.
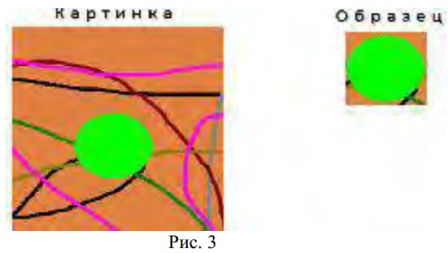
Видно, что по мере удаления от координат нахождения образца, коэффициент корреляции равномерно убывает. Следовательно, плавно убывает линейная связь между образцом и соответствующим участком изображения. Это означает, что если наш образец немного отличается от оригинала в изображении, например, он смещен на несколько пикселей, то программа все равно установит между ними связь. По итогам исследования можно сделать вывод, что с помощью коэффициента корреляции К. Пирсона можно установить линейную связь между пикселями изображения. И, таким образом, по величине коэффициента корреляции, мы можем судить о степени похожести двух изображений.