Реферат за темою випускної роботи
Ця робота знаходиться в стадії розробки. Більш детальна і кінцева інформація за цим проектом буде надана після завершення написання дипломної роботи.
Зміст
- Вступ
- 1. Постановка завдання
- 2. Методи обчислення температурного поля
- 3. Застосування нечіткої логіки
- Перелік посилань
Вступ
Розповсюдження тепла в різних середовищах чинить великий вплив на характер протікання багатьох важливих для практики процесів. Тому вивченню питань, пов'язаних з розповсюдженням тепла, присвячена величезна кількість робіт, як фізичних, так і математичних.
Серед завдань, пов'язаних з розповсюдженням тепла, виділяється важливий клас задач, в яких досліджувана речовина зазнає перетворення, в результаті чого вона переходить з однієї фази в іншу з виділенням або поглинанням тепла. Подібні завдання (вони називаються завданнями типу Стефана) виникають у випадках плавлення і затвердіння речовини.
Суттєвою рисою таких завдань є наявність рухомої поверхні розділу між двома фазами (рідкої і твердої), причому закон руху цієї поверхні заздалегідь невідомий і його слід визначати. Саме на цій поверхні відбувається поглинання або виділення тепла, пов'язане з фазовим переходом. Термічні властивості фаз по обидві сторони рухомої поверхні можуть виявитися різними. Завдання цього класу помітно складніші тих, в яких відсутній перехід речовини з однієї фази в іншу.
Важливим і цікавим завданням такого класу, якому присвячена дійсна робота, є завдання управління процесом кристалізації речовини.
Актуальність представленої роботи зумовлена як практичною затребуваністю нечіткого управління процесу кристалізації для об'єкта зі складною геометрією, так і необхідністю розробки методології чисельного рішення задачі оптимального управління цим процесом, що вносить вклад у теорію оптимізації складними динамічними системами.
Виникаючі практичні завдання вимагають не тільки опису та вивчення процесу кристалізації металу, а й оптимального управління цим процесом, тому що це дозволяє поліпшити якість одержуваних виробів і знизити витрати при відділенні виробу від форми.
1. Постановка завдання
Для визначення оптимальних теплофізичних умов формування злитка були проведені розрахунки в рамках математичної моделі теплових процесів в циліндричному злитку [1], адаптованої для випадку полого злитка (рис.1). У моделі, що використовується, рідкий метал зливається в кристалізатор порціями, а злиток з нього витягується періодично. Поверхня злитка обігрівається трьома електронними променями, причому потужність W3 одного з них рівномірно розподілена в центральній зоні (R2 < r < R1), а двох інших W1 та W2 сконцентрована в периферійних зонах. У математичній моделі контрольованими технологічними параметрами є: потужності променів W1, W2 та W3, періодичність заливки τ, висота порції h, яка одночасно зливається в кристалізатор, величина зміщення периферійного променя від центру на стінку кристалізатора d.
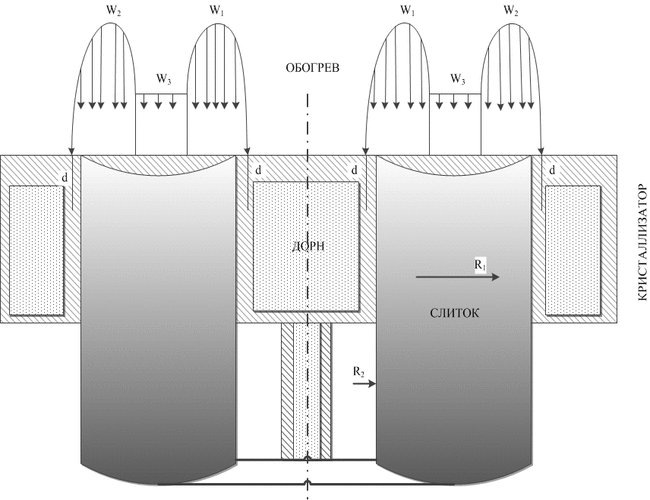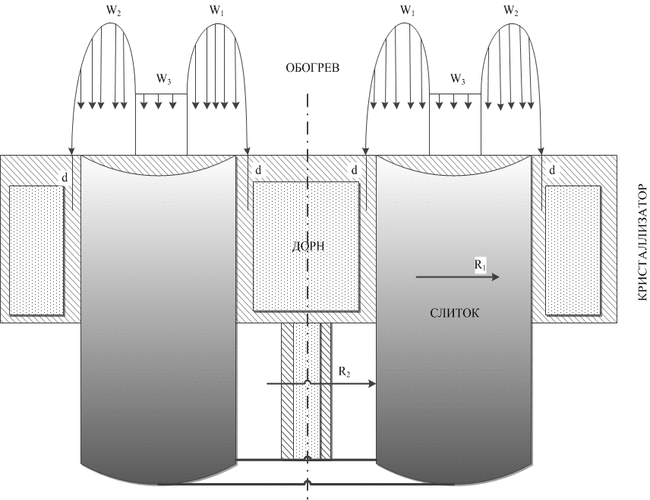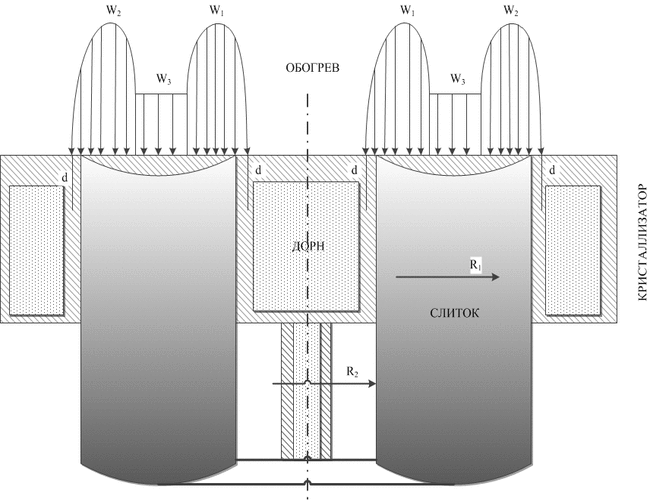
Рисунок 1 – Схема моделювання процесу формування полого злитка при ЕЛПЄ
Процес перенесення тепла описується рівнянням теплопровідності в циліндричній системі координат (r,O,z) випадку осьової симетрії. Ось OZ системи координат збігається з оссю злитка (ось симетрії), а ось OR – з радіальним напрямком. Початок координат заданий на нижній основі злитка.
Рівняння теплопровідності в цьому випадку приймає вигляд
де c – питома теплоємність; ρ – щільність; λ – коефіцієнт теплопровідності; R1 и R2 – зовнішній і внутрішній радіуси злитка; s(t) – поточна висота злитка.
При цьому гранична умова на внутрішній поверхні злитка – теплообмін зі стінкою дорна. Залежно від того, в якому співвідношенні знаходиться температура поверхні злитка з деякою критичною температурою TK (за якої поверхня злитка відділяється від стінки кристалізатора), теплообмін злитка з кристалізатором здійснюється за різними законами.
Під час T < TK – за законом Стефана-Больцмана
де ε – ступінь чорноти; σ – постійна Стефана-Больцмана; Tcρ – температура стінки кристалізатора.
При T > TK – за законом Ньютона-Ріхмана
де α – коефіцієнт теплопередачі між злитком і кристалізатором.
2. Методи обчислення температурного поля
Маємо наступні умови:
U = X(x), Y(y)
X = C1cosλx + C2sinλx
(– λC1sinλx + C2cosλx) ± ω0(C1cosλx + C2sinλx) = 0
λtgx = ω0, λ = λn
Y″ + ωY′ – λ2Y = 0, Y = eμy
μ2 + ωμ – λ2 = 0
У результаті розрахунків отримаємо наближення порядку n у загальному випадку за мінімізації функціоналу
Для оцінки похибки методу можна скористатися оцінкою:
3. Застосування нечіткої логіки
У дійсній роботі досліджується процес управління охолодженням рідкої речовини в ливарній формі, що має складну структуру. Остигання об'єкта відбувається в спеціальній установці, яка дозволяє управляти цим процесом. Об'єкти і установки, подібні розглянутим у роботі, використовуються в металургійній промисловості.
Нехай D = (–1 < x < 1, y < 0) півсмуга, заповнена твердим металом. Позначимо через u(x,y)температуру цього металу. Потрібно визначити температуру u(x,y) за наступними умовами:
ux ± ω0u = 0, x = ±1, (2)
u(x,–∞) = 0, (3)
uy(x,0) = ν(x), –1 ≤ x ≤ 1. (4)
Тут ω та ω0 – сталі, відповідно, число Пекле и Нуссельта. Рішення задачі (1–4) має вигляд
де , n = 1, 2, 3, …, λn – позитивні корені рівняння λ = ω0ctgλ.
Ототожнимо тепер температуру u(x,y) з температурою твердого злитка, що знаходиться в кристалізаторі при електронному переплаві. Для витягування злитка із кристалізатора поверхня злитка обігрівається трьома електронними променями W1, W2, W3, причому потужність W3 одного з них рівномірно розподілена в центральній зоні {–1 ≤ x ≤ 1, y = 0}, а два інших сконцентровані по шматках x = ±1. Незалежно від того, в якому відношенні знаходиться температура поверхні злитка з критичною температурою T*, за якої поверхня злитка відділяється від стінок кристалізатора, тим не менш, теплообмін злитка з кристалізатором здійснюється за формулою (2).Для отримання температури злитка досить покласти у формулі (5) ν(x) = (W1, W2, W3).
Далі введемо в розгляд функціонал
Розглядається наступна задача. Потрібно визначити потік ν(x) з допустимої множини U, який доставляє найменше значення функціоналу I(ν). Мінімізуюча послідовність νn будується за формулою νn+1 = νn + εn(νn–1 – νn), параметр εn вибирається з умови min0≤εn≤1I(νn–1–νn)). В якості області визначення функції U береться безліч кусочно-постійних східчастих функцій:
За цього формула (5) прийме вигляд:
а I(ν) = I(ν0,ν1, ν2, ..., νm).
За чисельної реалізації задачі необхідно врахувати обмеження 2500 ≤ ν(x) ≤ 5000,
тут ν(x) –потужність потоку в одиницях МВт/м2.
Нехай x1, x2, ..., xn – фактори, що впливають на процес кристалізації, а y1, y2, ..., yn – умови, при яких відбувається поява нового злитка. Тоді нечітке управління в даній задачі представляється у вигляді функціонального відображення X(x1, x2, ..., xn)→Y(y1, y2, ..., yn).
Заради простоти в якості терм-множин лінгвістичних змінних x1, x2, x3, где x1 = {"температура"}, x2 = {"спосіб нагріву"}, x3 = {"злиток металу"}, будемо використовувати множини:
T = {"мінімальна","середня","максимальна"},
W = {"мінімальний","середній","максимальний"},
L = {"мінімальний","середній","максимальний"}.
Таким чином, маємо x = (x1, x2, x3)→Y∈[α,β], де α та β – деякі числа (вони вибираються таким чином, щоб відбулося відділення злитка від стінок кристалізатор), а для вихідної лінгвістичної змінної Y (температура поверхні злитка) використовуватиметься терм-множина Q = {мінімальна","середня","максимальна"}.
Чисельний розрахунок, що дозволяє побудувати нечітке управління, здійснюється за допомогою алгоритму Мамдані. При цьому використовувалися такі значення параметрів: 400мм ≤ L ≤ 6000мм, 2500 Вт/м2 ≤ W ≤ 5000 Вт/м2.
Перелік посилань
- Жук Г.В., Ахонина Л.В., Тригуб Н.П. Математическое моделирование процессов кристаллизации титанового сплава Ti–6A1–4V при ЭЛПЕ // Там же. – 1998. – № 2 – С. 21–25.
- Миненко А.С., Шевченко А.И. Приближенный анализ пространственной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 10 – С. 29–33.
- Миненко А.С., Шевченко А.И. Приближенный анализ стационарной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 5 – С. 36–40.
- Миненко А.С., Шевченко А.И. Приближенный анализ многомерной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 4 – С. 30–34.
- Миненко А.С. Математическое моделирование процессов кристаллизации металла // Искусственный интеллект. – 2010. – № 2 – С. 37–43.
- Миненко А.С., Исследование стационарной конвективной математической модели кристаллизации вещества // Искусственный интеллект. – 2010. – № 1 – С. 103–107.
- Шевченко А.И., Миненко А.С. Математическое моделирование процессов кристаллизации металла с учетом конвекции и примесей // Доповіді НАН України. – 2011. – № 6 – С. 35–39.
- Миненко А.С., Шевченко А.И. Задача Стефана при наличии конвекции // Доповіді НАН України. – 2012. – № 1 – С. 35–39.
- Миненко А.С., Гунько С.А. Численный анализ конвективной модели кристаллизации // Искусственный интеллект. – 2012. – № 1 – С. 43–48.
- Миненко А.С. Приближенный анализ нелинейной конвективной математической модели // Искусственный интеллект. – 2012. – № 1 – С. 36–43.
- Миненко А.С., Павлыш В.Н. Применение математического моделирования в задачах управления информационными процессами с элементами нечеткой логики при автоматизации технических систем. // Збірник наукових праць Донецького державного університету управління. Серія:
Державне управління
. Випуск:Соціальний менеджмнет і управління інформаційними процесами
– Донецьк: ДонДУУ, 2010. – С. 43–48. - Миненко А.С., Волченко Е.В., Шишкин С.А. Метод построения взвешенных временных рядов для решения задачи прогнозирования // Східно-Європейський журнал передових технологій. – Харків, 2012. – № 2(56). – С. 20–34.
- Миненко А.С., Шевченко А.И. Методы исследования нелинейных математических моделей. – Київ: Наукова думка, 2012. – 130 с.
- Шевченко А.И., Миненко А.С., Золотухина О.А. Численный анализ одной нелинейной математической модели // Доповіді НАН України. – 2012. – № 10 – С. 35–38.
- Миненко А.С., Шевченко А.И. Методы исследования нелинейных математических моделей – Національна академія наук України Інститут проблем штучного інтелекту, Донецьк, 2012. – 132 с..
- Шевченко А.И., Миненко А.С. Математическое моделирование одного класса сложных систем с применением нечеткой логики // Доповіді НАН України. – 2013. – № 5 – С. 51–54.
- Шевченко А.И., Миненко А.С. Моделирование потенциально-вихревого течения со свободной границей с применением нечеткой логики // Доповіді НАН України. – 2013. – № 6 – С. 47–51.
- Шевченко А.И., Миненко А.С., Сыпко И.А. Моделирование одного класса сложных систем с нечетким управлением // Доповіді НАН України. – 2013. – № 8 – С. 52–54.
- Шевченко А.И., Миненко А.С. Об одном классе интегральных функционалов с неизвестной областью интегрирования // Доповіді НАН України. – 2013. – № 12 – С. 48–52.
- Миненко А.С., Шевченко А.И., Сыпко И.А., Гололобова А.С. Нечеткое управление в нелинейных теплофизических моделях. // Праці міжнародної конференції
Питання оптимізації обчислень
(ПОО-XL), К.: Інститут кібернетики ім. В.М. Глушкова, 2013. – С. 275–277.
