Реферат по теме выпускной работы
Данная работа находится в стадии разработки. Более детальная и конечная информация по данному проекту будет предоставлена после завершения написания дипломной работы.
Содержание
- Введение
- 1. Постановка задачи
- 2. Методы вычисления температурного поля
- 3. Применение нечеткой логики
- Список источников
Введение
Распространение тепла в различных средах оказывает большое влияние на характер протекания многих важных для практики процессов. Поэтому изучению вопросов, связанных с распространением тепла, посвящено огромное количество работ, как физических, так и математических.
Среди задач, связанных с распространением тепла, выделяется важный класс задач, в которых исследуемое вещество претерпевает превращения, в результате чего оно переходит из одной фазы в другую с выделением или поглощением тепла. Подобные задачи (они называются задачами типа Стефана) возникают в случаях плавления и затвердевания вещества.
Существенной чертой таких задач является наличие движущейся поверхности раздела между двумя фазами (жидкой и твердой), причем закон движения этой поверхности заранее неизвестен и его следует определять. Именно на этой поверхности происходит поглощение или выделение тепла, связанное с фазовым переходом. Термические свойства фаз по обе стороны движущейся поверхности могут оказаться различными. Задачи этого класса заметно сложнее тех, в которых отсутствует переход вещества из одной фазы в другую.
Важной и интересной задачей такого класса, которой посвящена настоящая работа, является задача управления процессом кристаллизации вещества.
Актуальность представленной работы обусловлена как практической востребованностью нечеткого управления процесса кристаллизации для объекта со сложной геометрией, так и необходимостью разработки методологии численного решения задачи оптимального управления этим процессом, что вносит вклад в теорию оптимизации сложными динамическими системами.
Возникающие практические задачи требуют не только описания и изучения процесса кристаллизации металла, но и оптимального управления этим процессом, т.к. это позволяет улучшить качество получаемых изделий и снизить расходы при отделении изделия от формы.
1. Постановка задачи
Для определения оптимальных теплофизических условий формирования слитка были проведены расчеты в рамках математической модели тепловых процессов в цилиндрическом слитке [1], адаптированной для случая полого слитка (рис.1). В используемой модели жидкий металл сливается в кристаллизатор порциями, а слиток из него вытягивается периодически. Поверхность слитка обогревается тремя электронными лучами, причем мощность W3 одного из них равномерно распределена в центральной зоне (R2 < r < R1), а двух других W1 и W2 сконцентрирована в периферийных зонах. В математической модели контролируемыми технологическими параметрами являются: мощности лучей W1, W2 и W3, периодичность заливки τ, высота одновременно сливаемой в кристаллизатор порции h, величина смещения периферийного луча от центра на стенку кристаллизатора d.
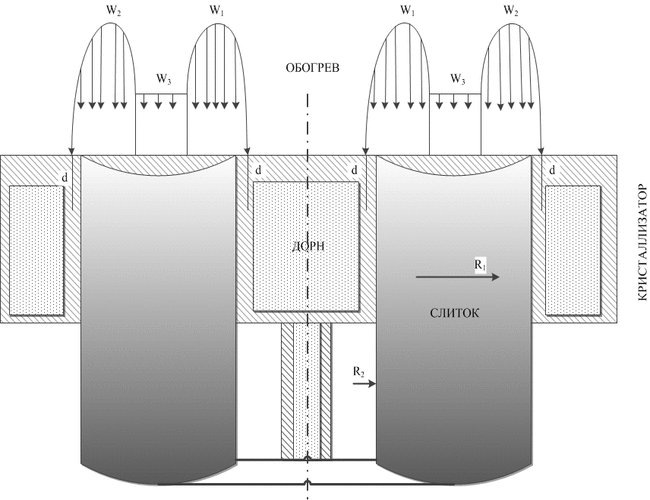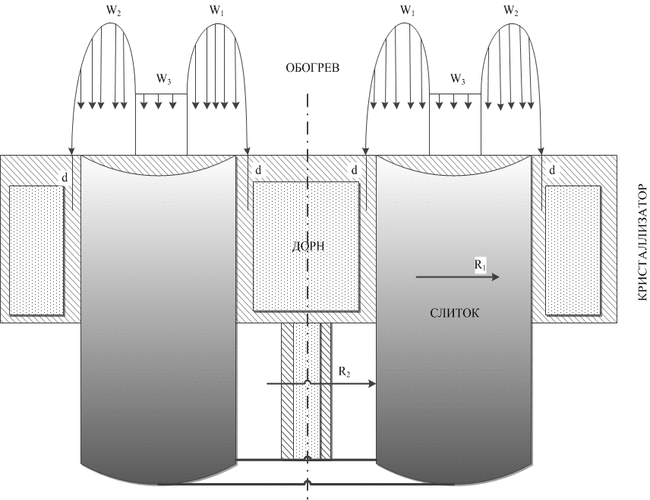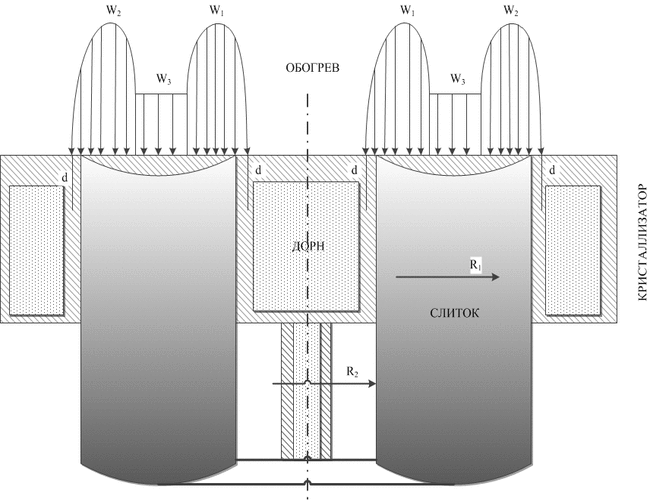
Рисунок 1 – Схема моделирования процесса формирования полого слитка при ЭЛПЕ
Процесс переноса тепла описывается уравнением теплопроводности в цилиндрической системе координат (r,O,z) для случая осевой симметрии. Ось OZ системы координат совпадает с осью слитка (ось симметрии), а ось OR – с радиальным направлением. Начало координат задано на нижнем основании слитка.
Уравнение теплопроводности в этом случае принимает вид
где c – удельная теплоемкость; ρ – плотность; λ – коэффициент теплопроводности; R1 и R2 – внешний и внутренний радиусы слитка; s(t) – текущая высота слитка.
При этом граничное условие на внутренней поверхности слитка – теплообмен со стенкой дорна. В зависимости от того, в каком соотношении находится температура поверхности слитка с некоторой критической температурой TK (при которой поверхность слитка отделяется от стенки кристаллизатора), теплообмен слитка с кристаллизатором осуществляется по разным законам.
При T < TK – по закону Стефана-Больцмана
где ε – степень черноты; σ – постоянная Стефана-Больцмана; Tcρ – температура стенки кристаллизатора.
При T > TK – по закону Ньютона-Рихмана
где α – коэффициент теплопередачи между слитком и кристаллизатором.
2. Методы вычисления температурного поля
Имеем следующие условия:
U = X(x), Y(y)
X = C1cosλx + C2sinλx
(– λC1sinλx + C2cosλx) ± ω0(C1cosλx + C2sinλx) = 0
λtgx = ω0, λ = λn
Y″ + ωY′ – λ2Y = 0, Y = eμy
μ2 + ωμ – λ2 = 0
В результате расчетов получим приближения порядка n в общем случае при минимизации функционала
Для оценки погрешности метода можно воспользоваться оценкой:
3. Применение нечеткой логики
В настоящей работе исследуется процесс управления остыванием жидкого вещества в литейной форме, имеющей сложную структуру. Остывание объекта происходит в специальной установке, которая позволяет управлять этим процессом. Объекты и установки, подобные рассматриваемым в работе, используются в металлургической промышленности.
Пусть D = (–1 < x < 1, y < 0) полуполоса, заполненная твердым металлом. Обозначим через u(x,y) температуру этого металла. Требуется определить температуру u(x,y) по следующим условиям:
ux ± ω0u = 0, x = ±1, (2)
u(x,–∞) = 0, (3)
uy(x,0) = ν(x), –1 ≤ x ≤ 1. (4)
Здесь ω и ω0 – постоянные, соответственно, число Пекле и Нуссельта. Решение задачи (1–4) имеет вид
где , n = 1, 2, 3, …, λn – положительные корни уравнения λ = ω0ctgλ.
Отождествим теперь температуру u(x,y) с температурой твердого слитка, находящегося в кристаллизаторе при электронном переплаве. Для вытаскивания слитка из кристаллизатора поверхность слитка обогревается тремя электронными лучами W1, W2, W3, причем мощность W3 одного из них равномерно распределена в центральной зоне {–1 ≤ x ≤ 1, y = 0}, а два других сконцентрированы по кускам x = ±1. Независимо от того, в каком отношении находится температура поверхности слитка с критической температурой T*, при которой поверхность слитка отделяется от стенок кристаллизатора, тем не менее теплообмен слитка с кристаллизатором осуществляется по формуле (2). Для получения температуры слитка достаточно положить в формуле (5) ν(x) = (W1, W2, W3).
Далее введем в рассмотрение функционал
Рассматривается задача. Требуется определить поток ν(x) из допустимого множества U, доставляющий наименьшее значение функционалу I(ν). Минимизирующая последовательность νn строится по формуле νn+1 = νn + εn(νn–1 – νn), параметр εn выбирается из условия min0≤εn≤1I(νn–1–νn)). В качестве области определения функции U берется множество кусочно-постоянных ступенчатых функций:
При этом формула (5) примет вид:
а I(ν) = I(ν0,ν1, ν2, ..., νm).
При численной реализации задачи необходимо учесть ограничение 2500 ≤ ν(x) ≤ 5000,
здесь ν(x) – мощность потока в единицах МВт/м2.
Пусть x1, x2, ..., xn – факторы, влияющие на процесс кристаллизации, а y1, y2, ..., yn – условия, при которых происходит появление нового слитка. Тогда нечеткое управление в данной задаче представляется в виде функционального отображения X(x1, x2, ..., xn)→Y(y1, y2, ..., yn).
Ради простоты в качестве терм-множества лингвистических переменных x1, x2, x3, где x1 = {"температура"}, x2 = {"способ нагрева"}, x3 = {"слиток металла"}, будем использовать множества:
T = {"минимальная","средняя","максимальная"},
W = {"минимальный","средний","максимальный"},
L = {"минимальный","средний","максимальный"}.
Таким образом, имеем x = (x1, x2, x3)→Y∈[α,β], где α и β – некоторые числа (они выбираются таким образом, чтобы произошло отделение слитка от стенок кристаллизатора), а для выходной лингвистической переменной Y (температура поверхности слитка) будет использоваться терм-множество Q = {"минимальная","средняя","максимальная"}.
Численный расчет, позволяющий построить нечеткое управление, осуществляется с помощью алгоритма Мамдани. При этом использовались следующие значения параметров: 400мм ≤ L ≤ 6000мм, 2500 Вт/м2 ≤ W ≤ 5000 Вт/м2.
Список источников
- Жук Г.В., Ахонина Л.В., Тригуб Н.П. Математическое моделирование процессов кристаллизации титанового сплава Ti–6A1–4V при ЭЛПЕ // Там же. – 1998. – № 2 – С. 21–25.
- Миненко А.С., Шевченко А.И. Приближенный анализ пространственной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 10 – С. 29–33.
- Миненко А.С., Шевченко А.И. Приближенный анализ стационарной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 5 – С. 36–40.
- Миненко А.С., Шевченко А.И. Приближенный анализ многомерной конвективной задачи Стефана // Доповіді НАН України. – 2010. – № 4 – С. 30–34.
- Миненко А.С. Математическое моделирование процессов кристаллизации металла // Искусственный интеллект. – 2010. – № 2 – С. 37–43.
- Миненко А.С., Исследование стационарной конвективной математической модели кристаллизации вещества // Искусственный интеллект. – 2010. – № 1 – С. 103–107.
- Шевченко А.И., Миненко А.С. Математическое моделирование процессов кристаллизации металла с учетом конвекции и примесей // Доповіді НАН України. – 2011. – № 6 – С. 35–39.
- Миненко А.С., Шевченко А.И. Задача Стефана при наличии конвекции // Доповіді НАН України. – 2012. – № 1 – С. 35–39.
- Миненко А.С., Гунько С.А. Численный анализ конвективной модели кристаллизации // Искусственный интеллект. – 2012. – № 1 – С. 43–48.
- Миненко А.С. Приближенный анализ нелинейной конвективной математической модели // Искусственный интеллект. – 2012. – № 1 – С. 36–43.
- Миненко А.С., Павлыш В.Н. Применение математического моделирования в задачах управления информационными процессами с элементами нечеткой логики при автоматизации технических систем. // Збірник наукових праць Донецького державного університету управління. Серія:
Державне управління
. Випуск:Соціальний менеджмнет і управління інформаційними процесами
– Донецьк: ДонДУУ, 2010. – С. 43–48. - Миненко А.С., Волченко Е.В., Шишкин С.А. Метод построения взвешенных временных рядов для решения задачи прогнозирования // Східно-Європейський журнал передових технологій. – Харків, 2012. – № 2(56). – С. 20–34.
- Миненко А.С., Шевченко А.И. Методы исследования нелинейных математических моделей. – Київ: Наукова думка, 2012. – 130 с.
- Шевченко А.И., Миненко А.С., Золотухина О.А. Численный анализ одной нелинейной математической модели // Доповіді НАН України. – 2012. – № 10 – С. 35–38.
- Миненко А.С., Шевченко А.И. Методы исследования нелинейных математических моделей – Національна академія наук України Інститут проблем штучного інтелекту, Донецьк, 2012. – 132 с..
- Шевченко А.И., Миненко А.С. Математическое моделирование одного класса сложных систем с применением нечеткой логики // Доповіді НАН України. – 2013. – № 5 – С. 51–54.
- Шевченко А.И., Миненко А.С. Моделирование потенциально-вихревого течения со свободной границей с применением нечеткой логики // Доповіді НАН України. – 2013. – № 6 – С. 47–51.
- Шевченко А.И., Миненко А.С., Сыпко И.А. Моделирование одного класса сложных систем с нечетким управлением // Доповіді НАН України. – 2013. – № 8 – С. 52–54.
- Шевченко А.И., Миненко А.С. Об одном классе интегральных функционалов с неизвестной областью интегрирования // Доповіді НАН України. – 2013. – № 12 – С. 48–52.
- Миненко А.С., Шевченко А.И., Сыпко И.А., Гололобова А.С. Нечеткое управление в нелинейных теплофизических моделях. // Праці міжнародної конференції
Питання оптимізації обчислень
(ПОО-XL), К.: Інститут кібернетики ім. В.М. Глушкова, 2013. – С. 275–277.
