
Ключевые слова: цифровая обработка изображений, коммутативные кольца, линейные операторы, нелинейная алгебра.
Введение Цель данной работы – рассмотрение двухэтапного алгоритма выделения контуров bitmap изображения.
На первом этапе под действием множества четырех линейных операторов, изображение преобразуется в множество четырех изображений тех же размеров, содержащих фрагменты контуров. Каждое из изображений множества содержит всю информацию об исходном изображении и может быть в него преобразовано одним из указанных линейных операторов в −1‑й степени. На втором этапе все соответствующие пиксели четырех полученных изображений складываются без изменения границ динамического диапазона.
С математической точки зрения цифровое изображение представляет собой матрицу, либо множество матриц одинаковых размеров с элементами из конечного алфавита. Если матрица изображения не одна, то описанные нами преобразования можно применить последовательно или параллельно ко всем этим матрицам. Поэтому без ограничения общности можно считать, что изображение – это матрица.

Элемент матрицы, то есть пиксель изображения X(m,n), принадлежит кольцу классов вычетов с основанием 2P:Z/(2P). Например, если изображение имеет форматbitmap в градациях серого, то P=8, а если полноцветный, то P=24. Предположим далее, что показатель степени P=QT, то есть не является простым числом. Тогда каждый элемент X(m,n) может быть представлен в 2Q‑ичной системе счисления:
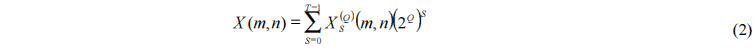
где
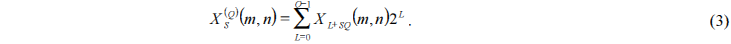
Такое представление позволяет рассматривать изображение как объединение слоев и соответственно по слоям проводить выделение контуров. При таком подходе каждый пиксель разбивается на T подпикселей, каждый из которых отвечает своему слою изображения. Два предельных случая соответствуют P слоям и двоичной арифметике или 1 слою и 2P‑ичной арифметике.
В процессе выполнения работы автор ознакомился с монографией (Фурман и др., 2002) и с ее обширным библиографическим списком. Желающие сравнить предлагаемый алгоритм с существующим многообразием алгоритмов выделения контуров могут воспользоваться этой монографией и ее ссылками.
Результаты работы докладывались на международной конференции (Zharkikh, 2007). В данный вариант работы внесены некоторые изменения, в частности, исправлены неточности и опечатки.
2. Алгоритм без потерь для выделения фрагментов контуров изображения (первый этап)
Введем простейшее семейство четырех операторов, отвечающих за выделение фрагментов контуров изображения.
Для каждого из четырех операторов выбираются множество пикселей матрицы изображения, которое не меняется данным оператором, и связанное с этим множеством направление преобразования. Из следующих формул понятно, что инвариантные множества – это нулевая или первая строка или нулевой или последний столбец изображения. В следующих формулах X, Y(*,*), S(*,*) – соответственно, матрица исходного изображения, матрица изображения фрагмента контура, оператор, формирующий изображение фрагмента контура из исходного изображения.

Параметры в записи операторов и выходных значений слоев пикселей обозначают следующее: Q – число бит в слое пикселя, L – движение слева (LEFT), R – движение справа (RIGHT), U – движение сверху (ABOVE), D – движение снизу (BELOW). Так условно можно представить перемещение вычислительной процедуры по слою пикселей изображения при действии соответствующего оператора.
Представленные операторы однозначно определены для заданного изображения и допускают возведение в любую целую степень и перемножение в любом количестве и любом порядке. Каждый из операторов с движением вдоль строк коммутирует с каждым оператором с движением вдоль столбцов. Операторы с параллельным движением попарно некоммутируют.
3. Алгоритм с потерями для объединения фрагментов контуров изображения (второй этап)
Первоначально автор обратил внимание на удобство использования конформных преобразований единичного круга для описания аналоговых сигналов с ограниченным динамическим диапазоном(Жарких, 1999а; Лаврентьев, Шабат, 1987). В работах(Жарких, 1999а; 1999b; 2001) анонсировалась возможность использования такой алгебры в задачах защиты информации.
Как показали теоретические расчеты и программная реализация, алгебраические операции, основанные на гомоморфизме X=th(x) (Жарких, 2005а), могут быть использованы для защиты звуковых сигналов (Жарких, 2003a; 2003b; 2005a; 2005с) и изображений (Zharkikh, Kolpakchi, 2004; 2006).
Рассмотрим гомоморфное отображение X=th(x) поля вещественных чисел на интервал(−1;1). Это отображение является изоморфизмом при подходящем выборе операций сложения и умножения. (Жарких, 2005а; Кириллов, 1978; Кострикин, 2000; Лаврентьев, Шабат, 1987). В данной работе операция умножения нас интересовать не будет, а операция сложения задается соотношениями (8) и(9):
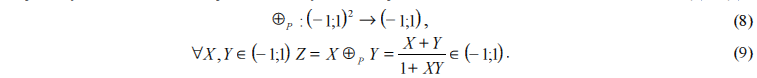
Операция (8) обладает гибридными свойствами.
При малых значениях аргументов это обычная операция сложения,
а на любом из двухэлементных множеств {0;+1} или {−1;0} –
это операция логическое или
(Жарких, 2005а).
В силу того, что значения пикселей изображения неотрицательные и
целые, операция (8) и (9) на основе масштабирования и взятия целой
части преобразуется к виду (10):
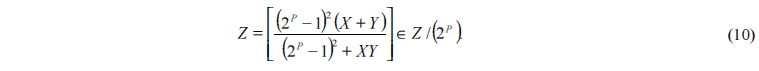

При сложении cоответствующих пикселей двух изображений согласно (10), изображения как бы склеиваются. Алгоритм объединения четырех фрагментов в один контур сводится к сложению их соответствующих пикселей согласно (10) в произвольном порядке.
4. Результаты применения алгоритма
На рис. 1–8 представлены результаты применения рассмотренного алгоритма. Все вычисления и визуализация выполнялись в пакете Matlab 7.0. Каждая цветовая компонента каждого пикселя рассматривалась как элемент кольца Z/(256), и вычисления проводились по модулю 256. Операторы (4) и (5) применялись к каждой паре соседних строк, а (6) и (7) – к каждой паре соседних столбцов. Масштаб преобразования был выбран равным 2.
Представленные иллюстрации хорошо отражают основные шаги алгоритма. На рис. 1 представлено исходное изображение. Это цифровая фотография рукописной буквы Ж каллиграфического текста. Изображение сохранено в формате полноцветного BMP. Его размеры 128 строк и 128 столбцов. Рис. 2–5 соответствуют первому этапу. Так как масштаб преобразования равен 2, инвариантные множества содержат 2 строки или 2 столбца. Это два начальных столбца, два конечных столбца, две начальные строки и две конечные строки для рис. 2, 3, 4 и 5 соответственно. Рис. 6–8 соответствуют второму этапу. Они визуализируют результат применения к изображения нелинейной операции сложения (10).
Этот, как и другие результаты работы алгоритма, подтверждают возможность его применения для выделения контуров на изображении.
5. Заключение
Алгоритм имеет линейную сложность по числу пикселей в изображении. Области применения и ограничения на использование рассмотренного алгоритма требуют дальнейшего изучения. По-видимому, он может эффективно использоваться в таких системах обработки и распознавания изображений, как медицинские, криминологические, геофизические, радиотехнические и др.
Радиолокация, навигация, связь, Воронеж, ВГУ, т.2, c.624–639, 2005a.
Идентификация систем и задачи управленияSICPRO'05. Москва, 25–28 января 2005 г. М., Институт проблем управления им. В. А. Трапезникова РАН, c.321–332, 2005b.
Математические методы распознавания образов, М., ВЦ РАН, с.305–307, 2003a.
Математические методы распознавания образов, М., ВЦ РАН, с.209–212, 2001.
Математические методы распознавания образов, М., ВЦ РАН, с.308–310, 2003b.
Радиолокация, навигация, связь, Воронеж, ВГУ, т.3, с.1886–1894, 1999b.