Генетические алгоритмы в составлении расписании при ограниченных ресурсах

Генетические алгоритмы в составлении расписании при ограниченных ресурсах

 

3. Связанные Работы

Различные вариации задач планирования с ограниченными ресурсами предложены, реализованы, и оцениваются уже на протяжении более пятидесяти лет. Методы решения образуют два различных класса: точные методы и эвристические методы. Эти классы могут быть отнесены далее к стохастическим и детерминированным подходам. Точные методы гарантирует найти решение, если оно существует, и, как правило, дают некоторый результат, если никакое решение не может быть найдено. Эвристические методы решения могут не давать такой гарантии, но, как правило, дают некоторую степень оптимальности в их решении. Стохастические методы включают вероятностные операции и два разных пути решения могут дать один результат. Детерминированные методы работают одинаково для одной задачи. Существуют гибридные методы, которые сочетают в себе характеристики обоих классов.

Когда для задач планирования с ограниченными ресурсами были впервые предложены простые модели, применили точные методы решения. Учитывая постановку задачи, точные методы могут найти наиболее лучшее решение с каждой итерацией. Однако, как только были добавлены ограничения, трудность решения задачи увеличивается, и нахождение лучшего решения стало проблематично. Кроме того, многие методы занимают слишком много времени, когда применяются к задачам большой размерности. Метод критического пути был разработан для нахождения кратчайшего времени.

Многие методы сосредоточены исключительно на планировании и предполагают, что план должен быть статическим. Стохастические модели добавили учет погрешности на реальных графиках. Более поздние методы пытались интегрировать планирование и найти оптимальное решение проблемы, которое используют преимущества связи между планами и графиками.

На рисунке 4 показаны три общие процедуры для решения задач составления расписаний при ограниченных ресурсов. Специфические вариации этих методов будут уточнены в разделах 3.2 и 3.3. Некоторые методы решения генерируют последовательности задач –– график работ, на основе этой последовательности (Рисунок 4a). Другие график работ, непосредственно, сосредотачивают внимание на других ограничений, таких как наличие ресурсов (рис. 4b). Некоторые методы комбинируют планирование и расписание, позволяя выбрать расписание из набора технологических планов (рис. 4c). Некоторые методы сосредоточиться на ресурсных ограничений, другие сосредоточены на старшинстве или временных ограничений. Некоторые детерминированы – они находят то же решение каждый раз, когда они запускают. Другие стохастические – они находят разное решение каждый раз, когда они запускаются. Многие методы являются гибридными и сочетают характеристики разных методов.

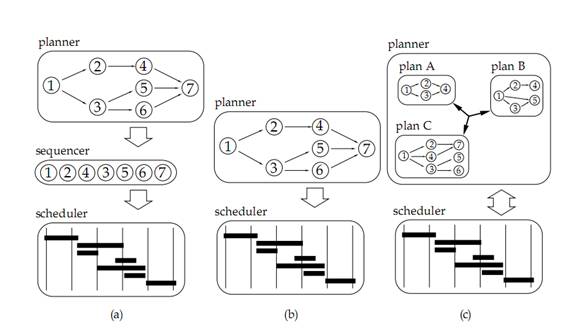
Рисунок 4. Общие методы для трех классов алгоритмов планирования

 

Планирование –– это определение ограничений и представление старшинства связей между задачами. Это назначение ресурсов к задачам в определенные моменты времени на диаграмме Ганта

 

3.1 Характеристика проблемы и задачи генерации

После пятидесяти лет исследований, направленных на решение задач составления расписаний, многие последние работы были посвящены описанию постановки задач. Цель этих исследований в том, чтобы понять структуру задач планирования, так что постановки задач могут быть созданы для того, чтобы тщательно протестировать множество методов решения. Определение проблемы и строительства проблемных генераторов тесно переплелись; наиболее проблемные генераторы включают в себя различные параметры, с которыми необходимо определить проблему, характеристики, но эти параметры часто характерны для определенной постановки или класса задач.

Одним из аспектов этой проблемы, с которыми сталкиваются те, кто пытается охарактеризовать задачи составления расписаний –– это огромное количество вариаций. Планирование задач принимает многие различные формы и размеры. Часто небольшое изменение приводит к совершенно новой постановке.

Многие задачи календарного планирования были описаны в литературе [Адамс и др., 1988] [Фишер и Томпсон, 1963] [Лоуренс, 1984] [Апплегэйт и Кук 1991] [Сторер и др., 1992] [Ямада и Накано, 1992]. Классическая проблема jobshop сначала была представленна Мутом и Томпсоном [Мут и Томпсон, 1963]. С тех пор многие другие предложили и решили множество более сложных изменений.

Несмотря на то, что много методов решения были опубликованы, сложность правильной постановки задачи была широко распространенной на общей базе тестовых задач. Кроме того, много методов решения были протестированы на проблемах от промышленных спонсоров, которые понятно беспокоятся о публикации деталей их операций.

 

3.2 Точные Методы решения

Точные методы гарантируют найти оптимальное решение, но обычно становятся непрактичными, когда сталкивающийся с проблемами значительного размера или большими наборами ограничений.

 

3.2.1 Метод критического пути

Метод критического пути (CPM) обеспечивает неограниченное ресурсом расписание для ряда ограниченных действий с детерминированными продолжительностями. Это дает самому короткому РАСПИСАНИЮ принятие бесконечных ресурсов. Несмотря на то, что полезный для получения общего представления о трудности выполнения плана, метод критического пути не считает временным или ограничения ресурса. Стохастические изменения [Нейман 90] [Словинский и Вегларз 89] и динамические изменения [Блазевич 83] были также созданы в попытке приблизить метод критического пути, моделируя предположения действительности. Эти методы включают вероятностные оценки срока выполнения задания.

 

3.2.2 Линейные и целочисленное программирование

Многие проблемы планирования могут быть сформулированы в традиционной форме линейного или целочисленного программирования, но только если сделаны значительные упрощения.

В целом, точные методы зависят от характеристик целевой функции (например, строго целочисленные значения) и определенных ограничительных формулировок (например, только однорежимные задачи). Как отметил Дэвис Лоуренс, многие ограничения, обычно найденные в реальных проблемах планирования, не подходят под традиционные исследования операций или математические методы программирования [Дэвис 85]. Кроме того, линейные формулировки программирования обычно хорошо не масштабируются, таким образом, они могут использоваться только для определенных классов задач или небольших проблем.

Динамический подход программирования был описан Хелдом и Карпом, в котором оптимальное расписание было поэтапно разработано с построением оптимального расписания для любых двух задач, расширяющих расписание, добавляя задачи, пока все задачи не будут запланированы [Хелд и Карп 62].

3.2.3 Ограниченное перечисление

Много методов решения ищут дерево решений, сгенерированное от отношений приоритета в плане проекта. Как показано в рисунке 5, корень дерева соответствует первой задаче. Второй уровень дерева - набор задач, которые могут быть запланированы, как только первая задача была запланирована и т.д. Заключительное дерево таким образом представляет выполнимый приоритетом набор последовательностей задачи. Любая из последовательностей корня к листу может тогда быть передана к генератору расписания. Альтернативно, последовательность задач может быть запланирована непосредственно, если древовидный алгоритм генерации/сокращения также рассмотрит ограничения ресурса. Поиск состоит из пересечения дерева, пока лучший путь корня к листу не найден. Исчисляющие методы обычно ограничиваются, используя эвристику, чтобы уменьшить размер дерева.

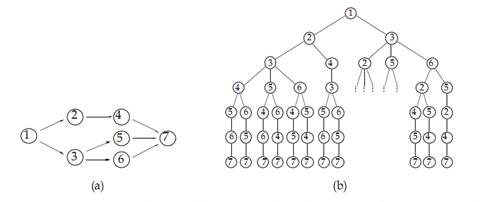
Рисунок 5 –– Генерация дерева возможных последовательностей из плана работ

a)                         ограничения управления очередностью показаны на для проекте с 7 задачами.

b)                         дерево управления приоритетами последовательностей для планирования 7 задач

 

Легко увидеть, как с увеличением числа задач быстро растет дерево. В зависимости от управления очередностью отношений, каждая новая задача может добавить много ветвей в дерево. Когда задачи моделируются с несколькими режимами выполнения, каждый режим выполнения добавляет еще один уровень комбинаторных вариантов для планировщика. Спречер и Дрексл отметили, что перечислительные методы могут решить проблему с различными функциями целей [Спречер и Дрексл 1996]. Тем не менее, изменения типов ограничений требует новый набор эвристик для шага планирования, или новый алгоритм для обрезки ветвей деревьев.

Изменения ответвлений и связанные методы решения были сначала предложены в 1960-х [Лолер и Вуд 66] [Джонсон 67] . Ответвление Стинсона и связанный подход генерации деревьев, планирование действий, запускающихся с первой задачей, добавляющей узел к дереву для каждой задачи, которая могла быть запланирована на основе ограниченных ресурсов [Стинсон и др. 78]. Границы на основе частичных расписаний использовались, чтобы сократить дерево поиска. Эвристика для расширения дерева использовала вектор шести мер.

Совсем недавно Спречер, Колиш, Дрексл и Паттерсон усовершенствовали алгоритмы обрезки так, чтобы оптимальные решения многорежимных задач планирования проекта (порядка 100 задач) могло быть найдено в меньше, чем через несколько секунд на персональных компьютерах.

Как отметил Спречер и Дрексл, перечислительные методы не могут решать большие задачи; дерево просто слишком большое. Но значительный прогресс был достигнут в методах обрезки ветвей и границ. Методы по-прежнему ограничены и они все еще требуют специальных эвристики для компенсации изменения в ограничении в ресурсах.