М., Автоматизация и современные технологии. 1999. № 9. С.32–34.(отсканировано) 

КОМПЛЕКСНАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПЕРАТИВНО-КАЛЕНДАРНОГО ПЛАНИРОВАНИЯ В ГИБКИХ КОМПЛЕКСАХ МЕХАНИЧЕСКОЙ ОБРАБОТКИ

P.P. Загидуллин

       Одним из основных требований, предъявляемых к подсистемам оперативно-календарного планирования (ОКП) в гибких производственных комплексах (ГПК) механической обработки, является точность формируемого расписания работ отдельных гибких производственных модулей и всего ГПК в целом. Точность любой модели, как правило, зависит от полноты ее представления, адекватности условиям реальной производственной системы. В большинстве моделей ОКП расписание традиционно строилось относительно основного класса обслуживающих устройств — гибких производственных модулей (ГПМ). Модель расписания, методика и алгоритм его формирования с учетом процессов переналадок ГПМ при выполнении различных партий деталей (так называемых партияопераций) и влияния других технологических факторов представлены в работе [1]. Данное расписание строится из предположения, что количество транспортных средств (робокары, роботизированные тележки и др.), применяемых для перевозки партияопераций между отдельными ГПМ, ГПМ и складом, является наперед заданной известной и достаточной величиной. Локальные методы определения количества ТС представлены в работе [2]. В то же время, в большинстве случаев, при формировании оптимального расписания работы ГПК необходимо учитывать транспортные средства (ТС), как обслуживающие устройства в общей модели планирования. В связи с этим возникает необходимость в разработке обобщенной математической модели ОКП для ГПК механической обработки. 
      На множестве номенклатуры деталей, представленном множеством единиц планирования (ЕП), которыми являются партияоперации, М{еij, m, i = 1, j = 1, hi} и множеством обслуживающих устройств, представленных множеством ГПМ и ТС — N{nk} U R{rl}, необходимо составить оптимальное расписание. Графическая интерпретация произвольной модели расписания для случая М{3 х 3}, N{3} и R{2} представлена на рисунке диаграммой Гантта. Как видно из диаграммы, основными потерями времени для каждого ГПМ в расписании ГПК O являются: t_перeijk — потери времени, связанные с наличием операций переналадок в ГПМ при поступлении новых партияопераций деталей; t_oce_ijk — потери времени, связанные с ожиданием партий деталей, находящихся в требуемый момент на обработке на предыдущей операции; t_0CTe_ijk — потери времени, связанные с ожиданием партий деталей, находящихся в процессе транспортирования; t_0Ce_ijk — потери времени, связанные с занятостью транспортных средств; - суммарное время простоя k-го ГПМ при обработке ЕП e_ijk.Тогда обобщенная математическая модель задачи ОКП имеет следующий вид: 

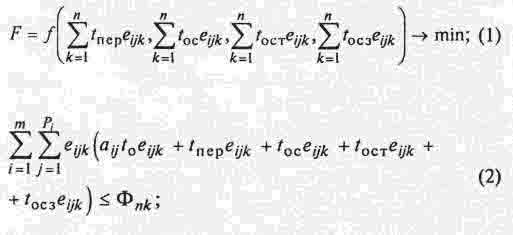
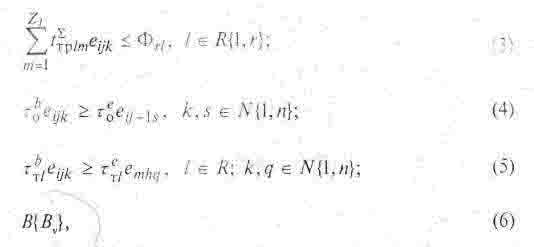
      где m > 1; n≥1; r≥1; аij = const — величина партии запуска ЕП; t_oe_ijk > 0 — время, отводимое на выполнение ЕП еij на k-м ГПМ; Pi≥1 —количество операции на i-й детали; Фnk — фонд времени работы k-го ГПМ на горизонте планирования; Фrl — фонд времени работы l-го ТС на горизонте планирования; Zl — количество заявок для l-го ТС на горизонте планирования. Горизонтом оси планирования может быть восьмичасовая смена. 
      Выражение (1) представляет собой функционал задачи в обобщенном виде, отражающий основные потери времени, а выражение (2) представляет собой ограничение по фонду времени работы ГПМ; выражение (3) отражает ограничение по фонду времени ТС; выражение (4) отражает выполнение условия предшествования для всех ЕП; выражение (5) отражает условие предшествования для ТС (ТС в том случае может обслужить заявку, если она на временной оси данного ТС не пересекается с любой другой заявкой, обслуживаемой данным ТС); выражение (6) представляет собой обобщенный состав дополнительных ограничений (ограничения по директивным срокам выпуска деталей и т.п.), что характеризует открытость математической модели. 
      Время обслуживания любым r-м ТС очередной заявки еij состоит из подготовительного времени t_ТПe_ijk, которое представляет собой время подхода ТС к требуемому ГПМ, времени загрузки-разгрузки ГПМ партией деталей и заключительного времени t_ТИrl — времени отхода ТС на промежуточную i-ю позицию. 
      Алгоритм формирования расписания ГПК для данной задачи, относящейся к классу NP-полных задач комбинаторного характера, представлен в работе [1]. 
      Обобщенный критерий задачи (1) в процессе моделирования заменяется одним из следующих конкретных критериев в зависимости от требований производства: 

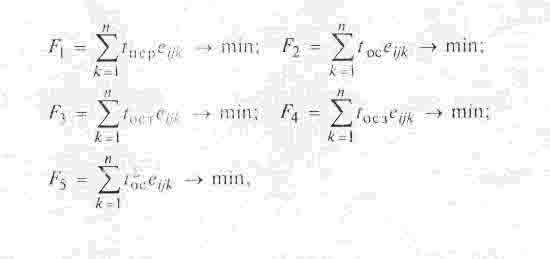
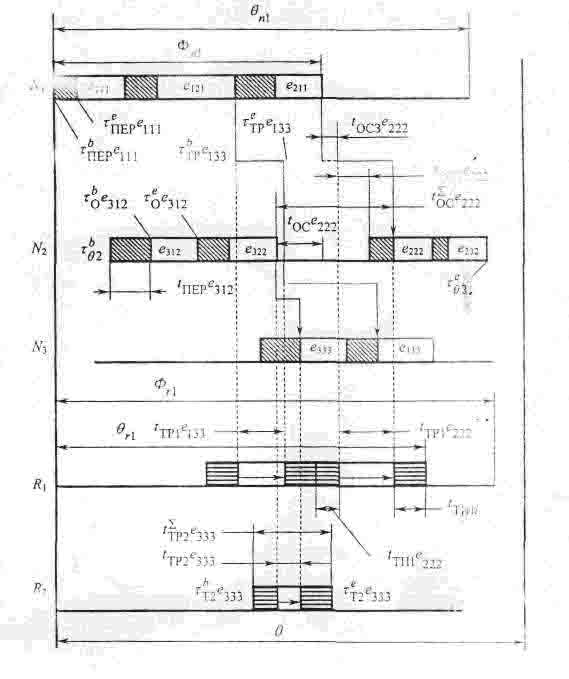
      Графическая интерпретация произвольной модели расписания.

      где F1, — критерий минимума времен переналадок в ГПМ; F2 — критерий минимума времен простоев ГПМ в ожидании поступления ЕП; F3 — критерии минимума времен простоев на транспортных операциях; F4 — критерий минимума времен простоев по причине занятости ТС; F5 — интегральный критерий минимума всех непроизводительных времен. 
      В результате работы алгоритма получается оптимальное расписание работы ГПК и подмножества оптимальных расписаний работы ГПМ и ТС: O {{On1, On2,…, Onn}, { Or1, Or2,…, Orr}}. 
      Таким образом, полученное расписание ГПК на заданном горизонте планирования и при текущем состоянии технологических ресурсов, имеющихся в ГПК, является оптимальным. 
      В заданной задаче были рассмотрены два основных класса обслуживающих устройств в ГПК – ГПМ и ТС. При наличии дополнительных обслуживающих устройств (станции мойки и сушки, контрольные позиции и др.) модель может быть дополнена ограничениями на данные устройства. Ограничения в подобных моделях, в первую очередь, должны касаться фондов времени любого класса обслуживающих устройств (аналогично ограничениям 2 и 3 в модели) и условий предшествования операций обслуживания (аналогично ограничениям 4 и 5).