Реферат за темою випускної роботи
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і завдання розробок і досліджень
- 3. Огляд досліджень і розробок по темі
- 4. Математична модель для аналізу перехідних процесів у системі власних потреб
- 5. Основний зміст роботи
- Висновки
- Перелік посилань
Вступ
При всіх змінах в електричної ланцюга: включення, виключення, короткому замиканні, коливаннях величини якого-небудь параметра і т. п. – в ній виникають перехідні процеси, які не можуть протікати миттєво, так як неможливо миттєве зміна енергії, запасеної в електромагнітному полі ланцюга. Таким чином, перехідний процес обумовлений невідповідністю величини запасеної енергії в магнітному полі котушки і електричному полі конденсатора її значенню для нового стану ланцюга.
При перехідних процесах можуть виникати великі перенапруги, сверхтоки, електромагнітні коливання, які можуть порушити роботу пристрою аж до виходу його з ладу. З іншого боку, перехідні процеси знаходять корисне практичне застосування, наприклад, у різного роду електронних генераторах. Все це обумовлює необхідність вивчення методів аналізу нестаціонарних режимів роботи ланцюга.
1. Актуальність теми
Розрахункові схеми електричних станцій великої потужності і систем елек-тропостачання промислових підприємств можуть досягати істотних розмірів і мати складну топологію. Так, наприклад, схема постійного струму одного з енергоблоків потужністю 800 МВт має 105 вузлів і 130 гілок, має радіальні, кільцеві й шлейфові ділянки.
У найбільш перспективних вітчизняних фірмах які займаються проектуван-ням і спорудженням електроенергетичних об'єктів для розрахунків струмів КЗ використовуються програми розрахунку на ПЕОМ. Але такі програми мають велику вартість.
В навчальних закладах промислові програми розрахунків, як правило, не можуть бути використані через їх велику вартість. З іншого боку програми розрахунків мають закриту структуру і не можуть бути ефективно використані в навчальному процесі.
2. Мета і завдання розробок і досліджень
- Мета роботи
- Ідея роботи
- Основні завдання досліджень
- Предмет досліджень
- Об'єкт досліджень
- Методика і методи досліджень
У зв'язку з реконструкцією обладнання на електричних станціях з'являється необхідність постійних перерахунків струмів КЗ. У ряді випадків розрахункові схеми є досить складними і виникає необхідність автоматизації процесу розра-хунку в них струмів КЗ. Метою роботи є вдосконалення програмного забезпечення кафедри Електричні станції
пов'язаного з розрахунком струмів КЗ.
Розрахунок струмів КЗ для схем електричних з'єднань з різними класами напруги (до і вище 1 кВ) на змінному та на постійному струмі по єдиній комп'ютерній технології з застосуванням матричних методів вузлових потенціалів.
Модернізація методів і алгоритмів програм розрахунку струмів КЗ з метою підвищення їх функціональних можливостей та надійності розрахунків.
Предметом дослідження є програмні продукти з відкритим побудовою алгоритмів, реалізація яких виконана в пакеті автоматизації математичних розрахунків MathCad.
Методи та алгоритми розрахунку струмів КЗ в електричних схемах змінного і постійного струму.
У даній роботі використовуються наступні методи:
1. методи матричного аналізу;
2. метод вузлових потенціалів у класичному вигляді і з використанням матриці вузлових опорів.
3. Огляд досліджень і розробок по темі
Програмний комплекс EnergyCS для проектування електроенергетичних систем Іванівського державного енергетичного університету.
У програмному комплексі EnergyCS задача розрахунку струмів короткого замикання вирішена в спеціальному модулі EnergyCS TKZ. Модель, яка використовується для розрахунку струмів короткого замикання, задовольняє самим жорстким вимогам, що пред'являються до розрахунків для вибору уставок релейних захистів. Токи гілок наводяться до своїх номінальної напруги. При цьому враховуються точні значення коефіцієнтів трансформації трансформаторів і зміни опорів обмоток при перемиканні відгалужень РПН і ПБВ. Розрахунок вузлових напруг при коротких замиканнях проводиться методом Гауса, по напруженням вузлів обчислюються струми в гілках. Для розрахунку ЕРС в початковий момент короткого замикання для системи, генераторів, синхронних і асинхронних двигунів у програмі використовуються напруги в усталеному режимі, що передує моменту виникнення короткого замикання, – результати розрахунку усталеного режиму з урахуванням регуляторів напруги та режиму по активнії та реактивнії потужності (відповідно до вимог ГОСТ). Насправді повний розрахунок усталеного режиму проводиться для кожного розрахунку струмів короткого замикання. Модуль EnergyCS TKZ не пов'язаний з модулем EnergyCS UR і може використо-вуватися цілком незалежно. Для отримання порівнянних результатів можна включити режим програми, при якому ЕРС розраховуються за номінальними параметрами – результати будуть відповідати отриманим іншим способом (наприклад, вручну або з використанням інших програм). Однак при цьому можна отримати завищені або занижені значення струмів короткого замикання. На сьогодні програмний комплекс EnergyCS дозволяє вирішувати наступні завдання в рамках розрахунків струмів короткого замикання:
- розрахунок початкових значень струмів трифазних коротких замикань в сложнозамкнутих мережах;
- розрахунок початкових значень струмів однофазних на землю коротких замикань;
- розрахунок початкових значень струмів двофазних на землю коротких замикань;
- розрахунок початкових значень струмів двофазних без землі коротких замикань;
- розрахунок струмів в тросах ліній при коротких замиканнях на землю і оцінка їх термічної стійкості;
- розрахунок ємнісних струмів однофазних замикань на землю в мережах з ізольованою нейтраллю;
- розрахунок ударних струмів коротких замикань при трифазних КЗ відповідно до ГОСТ 27514-87 [1];
- розрахунок значення періодичної і аперіодіческій складових струму КЗ в заданий момент часу;
- розрахунок діючого значення струму трифазного КЗ в момент відключення;
- розрахунок інтеграла Джоуля на момент відключення, а також термічно еквівалентного і еквівалентного односекундного струмів короткого замикання;
- побудова векторних діаграм струмів і напруг для довільних вузлів та довільних гілок мережі.
Програма дозволяє при заданій точці короткого замикання розглянути розподіл струмів і напруг по всіх гілках схеми, вивести в таблицю або на схему значення максимальних значень фазних струмів КЗ, струмів у всіх фазах, струмів по симетричним складовим, а також побудувати векторну діаграму струмів для вибраної гілки і векторну діаграму напруг для вибраного вузла.
Під час розрахунку несиметричного короткого замикання в заданій точці схема нульової послідовності формується автоматично. Формування схеми здійснюється на основі:
- топологічної структури розрахункової схеми;
- інформації про схему груп з'єднання обмоток трансформатора і режиму його нейтралі;
- інформації про взаємний вплив ВЛ, що проходять в загальних коридорах з урахуванням геометрії підвіски проводів на опорі;
- інформації про наявність і способі заземлення грозозахисних тросів.
Результати розрахунків можуть бути виведені безпосередньо на схему або в таблиці. Остаточні документи можна формувати з використанням MS Word на основі заздалегідь заготовлених шаблонів.
У програмі передбачено кілька варіантів представлення результатів розрахунку ТКЗ.
При першому варіанті розраховувач визначає вузел, в якому слід розглянути можливість короткого замикання. У результаті виходять струми короткого замикання в даному вузлі при трифазному, двофазному, однофазному і двофазному КЗ на землю, а також значення ударного струму та постійної часу затухання вільної складової. Для кожного виду КЗ у всіх гілках визначається розподіл струмів, а для всіх вузлів – залишкові напруги (рис 1).

Рисунок 1 – Результати розрахунку токорозподілу (ТКЗ) при коротком замиканні в одній точці
При другому варіанті програма виконує розрахунки ТКЗ для безлічі зазначених вузлових точок схеми. У цьому випадку на схему можуть бути виведені лише значення струмів у виділених вузлах, а в таблицю - струми у всіх виділених вузлах і прилеглих до них гілках. Крім початкових значень струмів КЗ для всіх видів пошкоджень, в таблицю виводяться режимні параметри для оцінки теплового та динамічного дії струмів трифазного КЗ, тобто для кожного примикання до вузла КЗ гілки виводяться результати розрахунку ударного струму, інтеграла Джоуля, термічно еквівалентного і еквівалентного односекундного струмів (рис 2).

Рисунок 2 – Результати розрахунку ТКЗ при коротком замиканні в декількох точках
Для розрахунків струмів КЗ з метою визначення уставок релейного захисту передбачено розрахунок струмів, що протікають через задану гілку при коротких замиканнях в заданій множині вузлів. Приклад таблиці наведено на рис 3.

Рисунок 3 – Токи короткого замикання в контрольній гілці
Розрахунки струмів замикання на землю для мереж з ізольованою нейтраллю виробляються топологічним методом у цьому ж модулі і можуть бути виведені на схему або в таблиці разом з результатами розрахунків ТКЗ.
Приклад розрахунку ТКЗ для системи власних потреб теплової електростанції показано на рис 4.

Рисунок 4 – Приклад розрахунку ТКЗ для системи власних потреб [2]
4. Математична модель для аналізу перехідних процесів у системі власних потреб
На рис. 5 зображена принципова схема електричної системи з асинхронними і синхронними електродвигунами.

Рисунок 5 – Вихідна принципова схема електричної системи (анимация: 5 кадров, 5 циклов повторения, 238 килобайт)
Розрахункову схему складають на основі заданої принципової схеми електричної системи і схем заміщення її окремих елементів, які з деякими спрощеннями використовуються в даній роботі.
Розрахункова схема заміщення представлена опорами (активним, індуктивним) і ЕРС системи, опорами вимикачів, шунта КЗ, заземлювача і опорами статора асинхронного і синхронного електродвигунів потужністю 4000 і 6000 КВт відповідно.
Математична модель, яка створена на основі повних диференціальних рівнянь, дозволяє досліджувати перехідні процеси в системі власних потреб ТЕС набагато точніше, ніж методики, засновані на найпростіших алгебраїчних рівняннях.
Дана робота спрямована на усунення недоліків спрощених методів розрахунку і для удосконалення реалізації математичних моделей.
Математична модель даної схеми складається з диференціальних рівнянь для її основних елементів.
Для опису асинхронного двигуна (АД) будемо використовувати його двоконтурну схему заміщення, яка дозволяє досить точно врахувати явище витиснення струму в роторі [3]. Будемо використовувати відомий метод отримання параметрів двоконтурної схеми заміщення на основі каталожних даних.
Диференціальні рівняння, що описують поведінку АД в перехідному режимі, в нерухомій системі координат можна представити як:
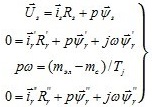
де:
 – результуючі вектори напруги, струмів і потокозчеплень статора і ротора;
– результуючі вектори напруги, струмів і потокозчеплень статора і ротора;
 – обертаючий момент двигуна і момент опору механізму;
– обертаючий момент двигуна і момент опору механізму;
Tj – постійна часу агрегату.
w – частота обертання ротора.
Явнополюсні синхронні двигуни, з метою можливості забезпечення асинхронного пуску забезпечуються пусковий обмоткою, стрижні якої закладаються в полюсні башмаки ротора і електрично з'єднуються між собою, а також зі стрижнями сусідніх полюсних башмаків. У результаті утворюється так звана повна пускова обмотка в осях d і q і обмотка збудження по осі d.
Визначення параметрів схем заміщення синхронної машини за каталожними даними.

Рисунок 6 – Схема заміщення явнополюсного синхронного двигуна по осі d [2]

Рисунок 7 – Схема заміщення явнополюсного синхронного двигуна по осі q [2]
Параметри обмотки збудження:

де:
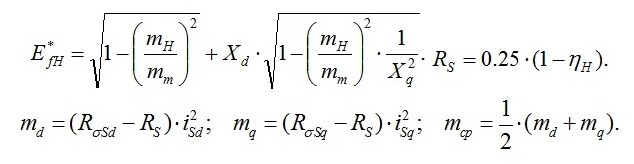
Математичне моделювання перехідних процесів проводиться для миттєвих значень струмів і напруг. Для цієї мети скористаємося законами Ома і Кірхгофа, згідно з якими потрібно скласти диференціальні рівняння для струмів і напруг гілок і вузлів заданої схеми. Алгоритми розрахунків складемо на основі матричних методів.
5. Основний зміст роботи
На eлектричних станціях великої потужності і систем електропостачання промислових прідприємств розрахункові схеми можут досягати значних размирів і мають складну топологію. На рис. 8 приведена схема електропостачання однієї з шахт Донбасу.

Рисунок 8 – Схема электропостачання однієї з шахт Донбасу
На рис. 9 преведена зпрощенна схема заміщення.

Рисунок 9 – Топологічная схема заміщення схеми електропостачання однієї з шахт Донбасу
У даній роботі пропонуються для розгляду програмні продукти з відкритим побудовою алгоритмів, реалізація яких виконана в пакеті автоматизації математичних розрахунків MathCad.
Як і при ручних розрахунках струмів КЗ на першому домашинному етапі робіт формується розрахункова електрична схема і відповідна їй еквівалентна схема заміщення. Для її елементів з довідкової літератури або інших джерел підбираються необхідні вхідні дані.
На еквівалентної схемою заміщення проводиться нумерація при невеликих схем, або символьна ідентифікація вузлів. Розмічаються також напрями струмів у гілках.
У програмі розрахунку струмів КЗ розрахункова схема представляється вхідною матрицею опису гілок V. Ця матриця має кількість рядків дорівнює кількості гілок розрахункової схеми, і кілька стовпців. У першому і другому з них розташовуються номери або позначення вузлів, з яких ток гілки виходить і в який цей струм входить. У наступному стовпці розташовуються опори гілок. При необхідності (у випадку різних величин) ще в одному стовпці розташовуються ЕРС гілок. Так, наприклад, в схемах головних електричних з'єднань електростанцій величина ЕРС генераторів може бути. порядку 1.2, а ЕРС електродвигунів – 0.9.
Алгоритми програм розрахунку струмів КЗ побудовані на методі вузлових напруг в матричній формі запису
 (1)
(1)
де Uu – вектор вузлових напруг, Yu – квадратна матриця вузлових провідностей, Iu – вектор вузлових струмів.
Матриця Yu знаходиться як
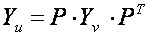 (2)
(2)
де P – матриця зв'язків вузлів з гілками, Yv – діагональна матриця провідностей гілок, Zv – вектор опорів, гілок, який повинен бути отриманий з вхідної матриці V.
Вектор Iu від ЕРС може бути знайдений як
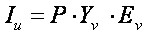 (3)
(3)
де Ev – вектор ЕРС гілок.
Матриця зв'язків Р в разі числової нумерації вузлів може бути створена за допомогою наступної функції користувача FormP
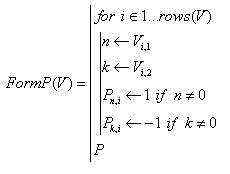 (4)
(4)
У разі ж символьної індексації вузлів у наведеній функції FormP будуть змінені умовні оператори на наступні:
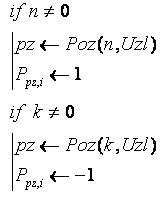 (5)
(5)
В операторах (5) використовується функція Poz для визначення номера вузла по його символьному позначенню у векторі Uzl.
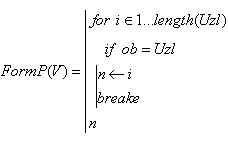 (6)
(6)
Вектор Uzl у випадку одного рівня напруги у вузлах розрахункової схеми, наприклад у схемах змінного і постійного струму напругою менше 1 кВ, формується автоматично з даних позначень вузлів матриці опису гілок V за допомогою наступної функції FormUzl

Рисунок 10 – Функція FormUzl для створення вектора Uzl
При розрахунку схеми з кількома ступенями напруги в якості вхідного формується матриця опису вузлів Ub, в якій в стовпцях розташовуються: позначення вузлі, величини середніх базисних напруг, власні tвв і повні tпв терміни відключення вимикачів і розрахунковий термін дії релейного захисту tрз.
Згідно ДСТУ 27514-87 Коротке замикання в електроустановках
[4] розрахунки сумарних значень періодичних складових струмів КЗ можуть бути отримані з використанням вхідних опорів схем по відношенню до відповідної точки КЗ. Зазначені опори можуть бути отримані в результаті звернення матриці вузлових провідностей розрахункової схеми Yu.
 (7)
(7)
Вони знаходяться у відповідних діагональних елементах матриці Zu. Струм КЗ в і-тому вузлі.
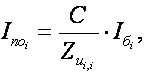 (8)
(8)
де C=1÷1.1; – еквівалентна ЕРС розрахункової схеми, Iб – базісний струм, Uб – базісна напруга.
За величиною Zu може бути також знайдена згідно [1] величина постійної часу в кожному вузлі розрахункової схеми як
 (9)
(9)
де w0 = 314.15 – синхронна кутова частота мережі
 (10)
(10)
Ударне миттєве значення струму КЗ.
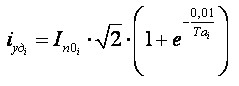 (11)
(11)
Тепловий імпульс струму КЗ.
 (12)
(12)
У тих випадках, коли необхідно знати розтікання струмів КЗ по гілках схеми, або коли величина ЕРС джерел значно відрізняються між собою розрахунок струмів КЗ в окремому вузлі Nk виконується в такій послідовності: у вузол КЗ вводиться шунт КЗ з великим значенням провідностей, наприклад
 (13)
(13)
Потім знаходяться напругу у вузлах по (1) і струми КЗ гілок, як
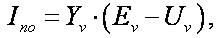 (14)
(14)
де Uv – вектор напруг гілок.
Сумарне значення періодичної складової може бути отримано, як
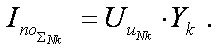 (15)
(15)
Розрахунок несиметричних КЗ. Згідно з правилом Щедріна точка КЗ умовно віддаляється на величину шунта КЗ і за ним розглядається симетричне КЗ. Величина шунт визначається результуючий опір схем зворотної та нульової послідовності. Для знаходження цих опорів формуються матриці опису гілок цих схем V2 і V0. Потім по них формуються матриці вузлових провідностей та опорів , як показано вище для схеми прямої послідовності. У відповідних діагональних елементах цих матриць знаходяться результуючі опору схеми по відношенню до відповідних вузлів. Струм несиметричного КЗ в і-тому вузлі знаходиться за наступним висловом.
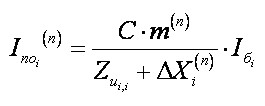 (16)
(16)
де m – коефіцієнт перерахунку між струмом прямої послідовності і струмом КЗ особливо фази Розрахунок струмів КЗ в електроустановках змінного струму напругою менше 1кв. Особливість цих розрахунків заключається в:
- облік активних опорів всіх елементів схеми;
- облік опорів електричної дуги;
- виконання розрахунків у іменованих одиницях;
- обов'язковий розрахунок трифазних і однофазних КЗ;
- облік опорів додаткових елементів схеми: трансформаторів струму, контактних з'єднань, котушок розчеплювача та інші.
У цілому ж алгоритм розрахунку істотно не відрізняється від описаного вище [4].
Выводы
В результаті виконання даної роботи можуть бути зроблені наступні основні висновки:
На основі розроблених методів машинного розрахунку струмів КЗ модернізована програма розрахунку на ПЕОМ в середовищі математичного пакета MathCad, яка має наступні переваги:
- можливість розрахунків симетричних і несиметричних струмів КЗ;
- введення індексної нумерації гілок.
Виконані зіставлення розрахунків струмів КЗ за розробленою програмою з кращими світовими аналогами дали позитивні результати.
По даній програмі були виконані розрахунки струмів КЗ для деяких електростанцій Донецького регіону.
Програма впроваджена в навчальний процес кафедри ЕС при виконанні курсового та дипломного проектування.
*При написанні даного реферату магістерська робота ще не завершена. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника в січні 2016 року.
Перелік джерел
- ГОСТ 27514-87. Короткое замыкание в електроустановках. Методы расчета в электроустановках переменного тока напряжением свыше 1кВ – М:.Издательство стандартов, 1988
- Николай Ильичев, Вячеслав Серов, Анатолий Кулешов, Ольга Михалева Программный комплекс EnergyCS для проектирования электроэнергетических систем.: CADmaster #36/1.2007 (январь-март) // Электротехника
- Скрипник О.І., Коновал В.С. Діалоговий автоматизований комплекс дакар – 2002 – новий рівень інформаційного забезпечення електроенергетичних систем.: Журнал
Вісник
Національного університетуЛьвівська політехніка
№ 460 2002 року - Крючков И.П., Неклепаев Б.Н., Старшинов В.А. Расчет коротких замыканий и выбор электрооборудования. М.: Академия, 2006.
