Применение метода интегральных нечетких взвешенных оценок при принятии решения

Аннотация

А.Н. Берёза, Е.А. Цвелик Применение метода интегральных нечетких взвешенных оценок при принятии решения Описан принцип предлагаемого метода расчета интегральных оценок на основе не- четких частных критериев с учетом коэффициентов их важности. Данный метод позволяет принимать решения при управлении сложными системами, характеристики которых невозможно оценить в количественных четких величинах. Описана архитектура системы поддержки принятия решения, которая реализует данный метод и апробирована на задаче принятия решения при планировании набора в вузе по различным образовательным программам и направлениям.
Ключевые слова: Нечеткие множества; деревья нечеткого вывода; интегральные оценки; системы поддержки принятия решения.

Введение

В управлении сложными системами применяются методы поддержки принятия решения и системы, автоматизирующие процесс принятия решения. Поскольку процессы и оценки их в сложных системах плохо формализуются, осуществляются в условиях неопределенности различной природы, принятие решения при управлении требует применения интеллектуальных методов [1]. Неопределенность среды, вызванная как сложностью количественных оценок, так и их субъективностью, не позволяет применять аналитические методы. Один из современных методов, используемых в различных задачах принятия решений, основан на применении аппарата теории нечетких множеств (ТНМ) и нечеткой логики [6, 7]. В задачах принятия решения в условиях неопределенности и методах, применяемых в них, применяются два основных подхода: 1) многокритериальная оптимизация, где осуществляется поиск решения в области D, полученной путем пересечения нечетких множеств, описывающих ограничения G и цели C задачи многокритериальной оптимизации:

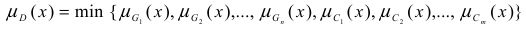
2) поиск решения с помощью алгоритмов нечеткого вывода, где условия поиска решения лежит обработка набора правил вида:

R1: ЕСЛИ x1 это A11 … И … xn это A1n, ТО y это B1

. . .

Ri: ЕСЛИ x1 это Ai1 … И … xn это Ain, ТО y это Bi

. . .

Rm: ЕСЛИ x1 это Ai1 … И … xn это Amn, ТО y это Bm,

где xk , k=1..n — входные переменные; y — выходная переменная; Aik — заданные нечеткие множества с функциями принадлежности.

Применение алгоритмов нечеткого вывода требует задания входных переменных в виде четких количественных оценок, для которых далее согласно этапам применения нечеткого вывода определяется степень принадлежности каждому терм-множеству. Для задач управления социально-экономическими системами получить четкие оценки параметров даже экспертным путем является сложной задачей, что ограничивает применимость систем поддержки принятия решения для этой сферы.

Кроме того, алгоритмы нечеткого вывода основаны на базе правил, в которой количество правил растет в геометрической прогрессии в зависимости от количества термов, определенных для каждой входной переменной и количества этих переменных. В результате говорят о «проклятии размерности». Выход из этой ситуации предлагается в виде применения деревьев нечеткого вывода, где критерии объединяются в группы и выстраиваются в иерархию, где на каждом уровне строится своя база правил и применяются алгоритмы нечеткого вывода.

Однако недостатком данного решения является необходимость фазификации и дефазификации входных переменных на каждом уровне иерархии в деревьях нечеткого вывода. «Недостаток этого способа состоит в том, что над промежуточными переменными последовательно выполняются операции дефаззификации и фаззификации. Нечеткие результаты промежуточных логических выводов дефаззифицируют, потом эти четкие значения подают на вход нечетких систем следующего уровня иерархии и там они фаззифицируются, т.е. становятся нечеткими. Следовательно, для промежуточных переменных надо задавать функции принадлежности. Кроме того, необходимо обеспечить эквивалентность нечетких множества до и после операций дефаззификации и фаззификации» [2]. Практика применения первого из указанных методов показывает, что в общем случае область, полученная путем пересечения нечетких множеств ограничений и целей, может оказаться пустой. И тогда, никакое приемлемое решение не может быть предложено. «Применение операции min — это отражение позиции «осторожного наблюдателя», когда все последующие решения принимаются из расчета на наихудший случай. Как отмечается в различных источниках, это может привести к созданию неоправданных резервов, а в некоторых случаях — и к параличу деловой активности. Известно также, что операцию min при свертке условий рекомендуется применять в условиях полной неопределенности, что для рассматриваемых задач не имеет места. Наконец, следует отметить, что использование операции min приводит к тому, что решение по существу принимается по одному критерию (условию), а не по всей их совокупности» [3].

Таким образом, необходимо предложить метод поиска интегральных оценок в деревьях поиска решений с соблюдением следующих требований:

• использованием нечетких оценок критериев;
• возможность учитывать степень влияния различных факторов на результат принятия решения;
• избежать необходимости фазификации и дефазификации на каждом уровне иерархии

Описание метода определения интегральных нечетких оценок на основе частных критериев.

В случае, если каждый критерий k будет оценен экспертом в виде нечеткого значения, то его оценка будет представлена в виде нечеткого множества с функцией принадлежности μk(x). Для каждого i-го критерия будет оценен

уровень его важности μki. Интегральный показатель на промежуточном уровне иерархии можно определить как нечеткое множество, полученное путем объединения нечетких множеств всех частных критериев с корректировкой на вес этого критерия:

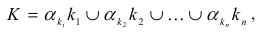
где K — нечеткое множество интегральной оценки на промежуточном уровне дере- ва нечеткой системы; ki — нечеткое множество, описывающее лингвистическую экспертную оценку частного критерия; μki — коэффициент важности данного критерия; n — количество критериев в группе. Функция принадлежности нечеткого множества интегрального показателя определяется по следующей формуле:

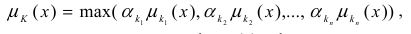
где μki — коэффициент важности критерия ki, μki(x) — функция принадлежности для выбранного лингвистического терма критерия ki, μk(x) — функция принадлежности для интегрального критерия.

Например, необходимо определить интегральную оценку K на основе трех частных критериев k1, k2. k3. Для каждого из критериев определены 5 лингвистических термов с функциями принадлежности μki(x). Веса критериев заданы соответственно для k1, k2. k3 — 0.3, 0.2, 0.5. Предполагается, что эксперт выбрал одну из лингвистических оценок (на рис. 1 выделены).

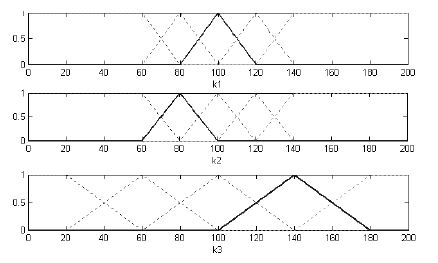
Рисунок 1 — Определение нечетких оценок для каждого из частных показателей

Функция принадлежности к нечеткому множеству общей интегральной оценки K будет иметь вид (рис. 2):

Рисунок 2. Построения нечеткого множества интегральной оценки

В процесс перехода от уровня к уровню процедура дефазификации не осуществляется вплоть до последнего верхнего уровня. Таким образом, можно избе- жать погрешности, накапливающейся от уровню к уровню в результате постоянных преобразований от нечетких значений к четким и обратно. Для применения алгоритма нечеткого вывода только на верхнем уровне иерархии необходимо произвести дефазификацию одним из известных способов, например, по методу определения центра тяжести. Для приведенного примера центр тяжести фигуры будет определен в точке, отображенной на рис. 3.

Рисунок 3 — Процедура дефазификации по методу определения центра тяжести

Таким образом, предложен метод расчета интегральных оценок на основе нечетких показателей с учетов критериев их важности. Данный метод был апробирован на задаче принятия решения о планировании набора абитуриентов в вузе, который является сложной социально-экономической системой. Для решения данной задачи была разработка системы поддержки принятия решений.

Описание системы поддержки принятия решения

Система поддержки принятия решения реализует предложенный метод на основе:

• базы правил для осуществления механизма нечеткого вывода на верхнем уровне иерархической модели;
• базы знаний в виде иерархии факторов и функций принадлежности для каждого значения данного фактора

Модель системы поддержки принятия решения включает в себя следующие блоки:

• блок формирования базы правил,
• блок определения коэффициентов важности факторов в иерархии,
• блок определения нечетких значений каждого фактора,
• блок расчета значений интегральных факторов в иерархии,
• блок нечеткого вывода.

На рис. 4 представлена структура системы поддержки принятия решения. Стрелками указана информация, которую необходимо ввести или получить из базы правил и базы знаний, для выполнения функций блока. Результатом работы системы является числовое значение выходной переменной блока нечеткого вывода — коэффициент корректировки плана набора. Реализация данной структуры была выполнена в системе MatLab 2009.

Перечень критериев для данной задачи: x1 — обеспеченность дисциплин преподавателями, x2 — общая остепененность преподавателей, x3 –доля преподавателей со степенью доктора наук, x4 - книгообеспеченность библиотечным фондом, x5 — обеспеченность методическими разработками и монографиями, x6 — электронные библиотеки и базы знаний, x7 — программное обеспечение, x8 — учебные площади, x9 — лабораторная база и специализированное оборудование, x10 — общежитие, x11 — мед. пункт, x12 — пункт питания, x13 — обеспеченность базами практик, x14 — спрос на образовательные услуги, x15 — спрос на специалистов на рынке труда.

Для каждого из них были сформированы лингвистические термы. Данные критерии были объединены в интегральные показатели следующим образом:

Данная иерархическая нечеткая система будет включать следующие подсистемы:

y1 — кадровое обеспечение, y1= f1(x1, x2, x3);

y2 — информационно- методическое, y2= f2(x4, x5, x6, x7);

y3 — материально-техническое, y3= f3(x8, x9);

y4 — социальное, y4= f4(x10, x11, x12);

y5 — общая ресурсообеспеченность, y5= f5(y1, y2, y3, y4, x13).

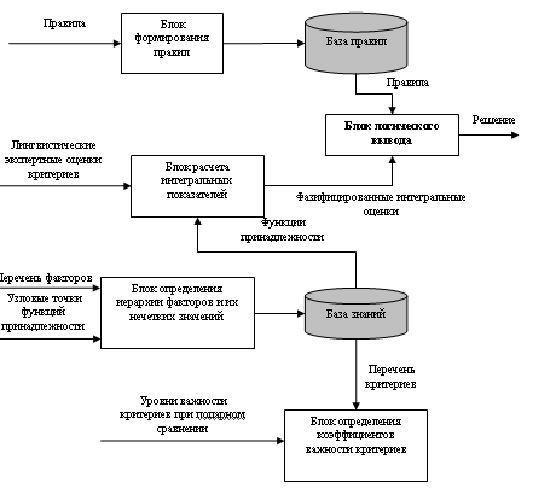
Рисунок 4 — Структура системы поддержки принятия решения

При построении функций принадлежности каждого нечеткого значения при- веденных критериев пользователем задаются узловые точки, и по ним строится классификатор. Однако, в отличие от стандартного пятиуровневого нечеткого 01-классификатора, мы не ограничивались отрезком [0, 1], так как для нахождения интегральных оценок не использовали матричную схему агрегирования. Была определена шкала от 0 до 200, где 100 — обозначает 100 % выполнение норматива и функция принадлежности терма «норма» в этой точке равна 1. Далее, исходя из допустимых отклонений при лицензировании, были определены узловые точки, которые могли быть разными для разных критериев. По этим узловым точкам построены треугольные и трапециевидные функции принадлежности для всех термов. При этом соблюдены требования стандартных классификаторов — сумма всех функций принадлежности для любого х равна единице. Примеры построения графиков функций принадлежности для критериев кадровой обеспеченности на рис. 5.

Аналогично строились функции принадлежности для остальных термов всех критериев, предусмотренных моделью.

Для расчета интегрального показателя использовалось диалоговое окно «Анализ ресурсообеспеченности», где пользователю предоставлена возможность определить лингвистические значения каждого критерия (рис. 6). В результате расчетов был получен интегральный показатель ресурсообеспеченности, равный 88.8823.

Рисунок 5 — Построение графиков функций принадлежности для лингвистических оценок кадровой обеспеченности

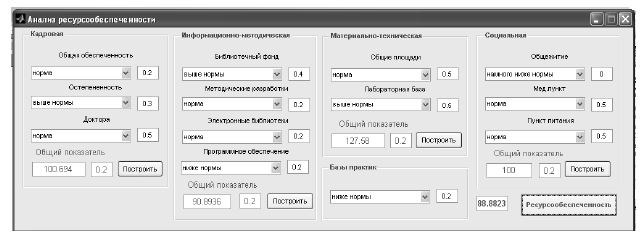
Рисунок 6 — Диалоговое окно «Анализ ресурсообеспеченности»

В примере значения показателей спроса были получены экспертным путем в виде числовых значений. В отдельном диалогов окне вызова системы нечеткого вывода (рис. 7) указываются рассчитанное значение ресурсообеспеченности и эксперт- ные оценки спроса на выпускников на рынке труда и спроса на образовательные услуги, которые являются входными переменными для блока нечеткого вывода.

Рисунок 7 — Диалоговое окно определения входных параметров для системы нечеткого вывода

В результате запуска блока нечеткого вывода появляется расчетное значение выходной переменной, которая определяет коэффициент в процентах изменения плана набора. В нашем случае, это приблизительно 94 %, что к имеющемуся плану 50 человек на исследуемое направление обозначает уменьшение плана на 3 человека, что не является существенным, следовательно, в целом, план набора можно сохранить.

Таким образом, разработанная советующая информационная система на основе модернизированного алгоритма нечеткого вывода формирует решение на основе имеющихся лингвистических оценок входных параметров: показателей ресурсообеспеченности образовательной программы, спроса на образовательные услуги и прогнозируемого спроса на специалистов – выпускников данного направления

Заключение

Применение предложенного метода расчета интегральных оценок позволяет в процессе принятия решения оперировать нечеткими оценками экспертов, избежать появления погрешности, которые могли бы появиться в случае применения деревьев нечеткого вывода. Кроме того, данная методика позволяет снизить трудоемкость при проектировании системы из-за отсутствия необходимости разрабатывать базы правил для каждого уровня иерархии системы нечеткого вывода.

Список использованной литературы

1. Н.Л. Келлер, М.Г. Гриф Интеллектуальная поддержка управленческих решений в вузе (на примере структурных преобразований) // Университетское управление: практика и анализ. – 2010. – № 2. – С. 16-23
2. С.Д. Штовба Введение в теорию нечетких множеств и нечеткую логику URL: http:// matlab.exponenta.ru/fuzzylogic/ book1/4_6.php.
3. В.Г. Чернов Решение задач многокритериального альтернативного выбора на основе геометрической проекции нечетких множеств // Информационно-управляющие систе- мы. – 2007. – № 1. – С. 46-51.
4. А.О. Недосекин Финансовый менеджмент. FUZZY FINANCIAL MANAGEMENT. – М.: AFA Library. – 2003. – 560 с.
5. С.А. Орловский Проблемы принятия решений при нечеткой исходной информации. – М.: Наука, 1981. – 206 с.
6. В.М. Курейчик Оптические системы с нечеткой логикой в задачах адаптивного модели- рования слабоформализованных процессов // Известия РАН «Теория и системы управ- ления». – М., 2011. – № 3. – С. 111-121.
7. В.М. Курейчик Оптонечеткие системы // Известия ЮФУ. Технические науки. Тематиче- ский выпуск «Интеллектуальные САПР». – Таганрог: Изд-во ТТИ ЮФУ, 2009. ? № 4. ? С. 99-106.