Новый алгоритм для нечеткого многокритериального принятия решений

Аннотация

T.Y. Tseng, Cerry M. Klein Новый алгоритм для нечеткого многокритериального принятия решений Алгоритм нечеткого многокритериального принятия решений позволяет использовать языковые рейтинги так же, как и числовые рейтинги. Этот алгоритм основан на преимуществе средневзвешенных методах рейтинговых и подразумеваемых методов сопряжения. Предложенный алгоритм протестирован на ровне с другими методами, а также показано насколько он точен и эффективен.

Ключевые слова: многокритериальное нечеткое принятие решений, лингвистические рейтинги, числовые рейтинги, нечеткие средневзвешенные, подразумеваемое объединение

Введение

Теория нечетких наборов была впервые предложен для принятия решений Беллманом и Заде [1]. С тех пор, применение теории нечетких множеств для принятия решений в нечеткой среде была проблема многих исследований. Например, Циммерман [3] работал над нечетким линейным программированием с несколькими целевыми функциями, в то время как Белин [4] обратился к нечеткому групповому принятию решений. Основной предпосылкой за этих двух научно-исследовательских работ было то, что является более целесообразным – иметь дело с нечеткими множествами, чем теории вероятностей. Бездек и другие [5] показывают потребность в использование нечетких множеств в условиях группового принятия решений. Этот настройки легко расширить для человека. Как отмечают они, когда ЛПР получает набор альтернатив, оно стремится посмотреть его как список взаимоисключающих элементов; оно должно действительно выбрать только один. В случае с нечеткими множествами допускается некоторая свобода, а также в процессе принятия оно регулирует свои взгляды на альтернативные варианты. Этот тип эволюции и альтернативного рассмотрения может быть наиболее легко обработать нечеткие множества, потому что предпочтение на "консенсусе" не определено. Единственная трудность, чтобы получить соответствующие «нечеткие предпочтения" от решения. Бездек и другие [6] дают динамический подход к обработке этого сценария. Большинство опубликованных работ со времен Беллмана и Заде используют схемы нечетких предпочтений и состоят в нахождении лучшего варианта среди доступных альтернатив при данных нескольких критериях в этой нечеткой среде. Этот поиск наилучшей альтернативы, как правило производился по одному из двух разных подходов: Беллмана-Заде или подразумеваемых метод соединения и метод средневзвешенный рейтинг.

Справочная информация

Многокритериальное принятие решений состоит в выборе лучшей альтернативы из множества альтернатив. Простой, но хорошо известный и часто используемый подход для решения многокритериальных задач принятия решений состоит в том, чтобы определить рейтинг средней взвешенной для каждой альтернативы, а затем выбрать лучший вариант, основываясь на этих рейтингах. Это делается следующим образом. Пусть A = { A₁, A₂ ..... A_m} } множество альтернатив m, которые должны быть сопоставлены. Все варианты оправданы с точки зрения набора критериев n C₁, C₂ ..... Cn Каждый критерий, связанный с взвешенным коэффициентом W_j, j = 1 ..... п, который присваивается в соответствии со степенью важность критерия C_j среди множества критериев. Относительная заслуга критерия C_j к альтернативной A_i оценивается коэффициентом рейтинг R_ij. В соответствии с этим методом добавочной взвешенной, альтернатива А_i можно расчитать взвешенный рейтинг R_i, где

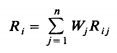
Если Ri нормализуется, альтернатива Аi получает средневзвешенной рейтинг

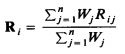
Предложенный новый алгоритм и методология

Нечеткие оценки, используемые в методе средних взвешенных рейтинга обсуждается в предыдущем разделе. Однако, несмотря на то что нечеткие рейтинги используются в числовом или словесном представлении, методы для каждого не являются взаимозаменяемыми. Словесные нечетких оценоки, используемые для метода средневзвешенного рейтинга должны быть определены математической функцией принадлежности. Тем не менее, для нечетких лингвистических оценок, для реализации объединения используется упорядоченная информация. Таким образом, подразумеваемый подход имеет недостаток, заключающийся в меньшей точности и меньшей надежности. Таким образом, представляется целесообразным разработать новый алгоритм, который позволит объединить преимущества метода средневзвешенного рейтинга и подразумеваемого метода объединения. То есть, алгоритм должен использовать нечеткую лингвистическую оценку, с математически определенной функцией принадлежности преобразовать нечеткий лингвистический рейтинг в нечеткое числовое значение, и применить метод подразумеваемых конъюнкций или взвешенной средней оценки, чтобы найти оптимальное решение в задаче многокритериального принятия нечеткой. Принимая эти три условия во внимание, алгоритм будет разработан в этом разделе. Обратите внимание, что нечеткая лингвистическая оценка, которая является нечетким подмножеством, будет рассматриваться как нечеткое число. Условия нечеткой лингвистической оценки и нечеткого числа будут использоваться как взаимозаменяемые.

Предлагаемый алгоритм основан на методе средней взвешенной. Для использования метода с наибольшей выгодой, переход от нечетких лингвистических оценок к нечеткому числовому значению необходим. Есть несколько способов, чтобы преобразовать нечеткую лингвистическую оценку в нечеткое числовое значение. Например, пик нечеткой лингвистической оценки или нечеткого числа может быть использованы для преобразования. Предлагаемые преобразования, однако, используют центр области, которая покрывает нечеткое число для представления перехода от нечетких лингвистических оценок к нечеткому числовому значению. Этот тип преобразования был выбран потому, что он, в большинстве случаев, чувствителен и способен реагировать на изменения в нечетких числах. Эта чувствительность позволяет легко описывать большинство нечетких чисел, что занимает центральное место в преобразовании нечеткой лингвистической оценки в нечеткое числовое значение.

ОПРЕДЕЛЕНИЕ 1. Пусть A = { A_l ..... A_i ..... A_n} набор нечетких лингвистических оценок или нечетких чисел на числовой прямой R. u_Ai(u) степень принадлежности u к A_i. Затем преобразование u(A_i) в A_i из нечеткой лингвистической оценки к нечеткому числовому значению, определяется следующим образом.

Модель 1:

Модель 2:

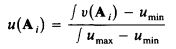
где

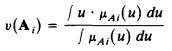
и

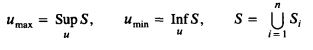
и

Тогда степень принадлежности uAi от Ai для каждой модели нечеткого числового значения обозначается

Таким образом, после преобразования, нечеткая лингвистическая оценка Ai будет нечетким синглтоном, который имеет только одну точку в нечетком множестве. Нечеткий синглтон преобразования нечеткой лингвистической оценки Ai, может быть выражена как

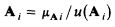
Так нечеткие лингвистические оценки или нечеткие числа принято считать дугообразными и нормальными, A_i может быть выражена как A_i = 1 / u(A_i) – Следовательно, средневзвешенная операция в нечетком многокритериальном принятии решений может быть определена следующим образом.

ОПРЕДЕЛЕНИЕ 2. Пусть B₁, B₂ .... , B_m альтернативы оценки по критериям C₁, C₂ ..... C_n Тогда для данного варианта B_i относительно заслуга критерия C_j оценивается нечетким лингвистическим рейтинг r_ij, Кроме того, относительная важность каждого критерия оценивается коэффициентом взвешивания w_j для критерий C_j. Тогда альтернатива B_i получит средневзвешенный рейтинг r_i, который обозначается

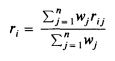
Когда w_j и r_ij представлены нечеткими числами, w_j и r_ij могут быть преобразована в w_j и r_ij по Определению 1, и преобразуется средневзвешенный r_i обозначается как

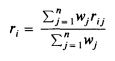
Рейтинг альтернатив B₁, B₂ ..... B_m может быть составлен следующим образом.

ОПРЕДЕЛЕНИЕ 3. Пусть преобразованные средние взвешенные r₁, r₂ ..... r_m из альтернатив B₁, B₂ ..... B_m получены из определения 2. Тогда для выбора из двух любых альтернатив B_i и B_j определяется r_i и r_j , То есть, если r_i больше r_j, то B_i предпочтительнее B_j. Приведенные выше определения приводят к следующему алгоритму.

Предложенный метод средневзвешенной

1. Преобразование каждого нечеткого элемента нечетких лингвистических оценок в числовое значения (модель 1 или 2 модели Определения 1).
2. Оценка каждого варианта по средневзвешенному уравнения (Определение 2).
3. Ранжирование альтернатив (Определение 3).

Оценка и сопоставление предлагаемого метода средневзвешенной и FWA алгоритма

Чтобы оценить и сравнить эффективности предложенного метода средневзвешенной и алгоритма FWA, будут использованы два фактора, эффективности и действенности.

Оценка эффективности двух входных наборов в модели 1 (1000 тестовых прогонов).

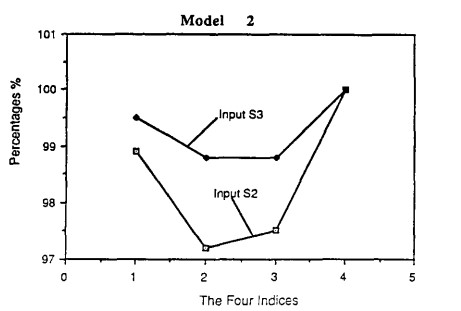
Оценка эффективности двух входных наборов в модели 2 (1000 тестовых прогонов).

Предлагаемые возвращаемые результаты алгоритма очень близкие к тому, что и в алгоритме FWA. Далее приводится сравнение эффективности алгоритма FWA и метода средневзвешенной оценки. Таблица 1 дает сводную статистику процессорного времени, потребляемого предложенным алгоритмом для двух моделей трансформации и алгоритма FWA на 1000 тестовых наборах, на входе $ 2 и $ 3. Для алгоритма FWA, измеряется время процессора только для шагов 1-8. Процессорное время для шага 7 в программе / GRAPH SAS была вычислена только для 100 тестовых прогонов, а затем умножается на 10, чтобы приблизить значение на 1000 тестах в эксперименте. Обратите внимание, что время процессора измерялась компилятором уровня 0 для программы Fortran и с графическим терминалом для программы / GRAPH SAS под скорость высокопроизводительной ЭВМ IBM IBM 3179.

Таблица 1. Сравнение времени процессора для моделей 1 и 2 метода средневзвешенной и FWA алгоритма на 1000 тестовых прогонов

Как указано в таблице 1, экономия процессорного времени для моделей 1 и 2 предлагаемого метода средневзвешенной по сравнению с алгоритмом FWA является чрезвычайно значимой. Это указывает на то, что предлагаемый способ, использующий средние взвешенные Модели 1 и 2 является очень эффективным. На основе оценки моделей 1 и 2 и на сравнении моделей 1 и 2 с алгоритмом FWA, можно сделать вывод, что модели 1 и 2 предлагаемого способа средних взвешенных являются двумя действенными и эффективными методами оценки проблемы нечетких многокритериальных принятий решений.

Выводы

В статье предложен новый алгоритм на основе трансформации модели для решения нечетких многокритериальных задач принятия решений. Новый алгоритм основан на преобразовании нечеткого лингвистического рейтинге и на средневзвешенном методе многокритериального принятия решений.

Производительность каждой из моделей была протестирована на проблемы прототипа с помощью трех наборов нечетких лингвистических оценок. Этот тест состоял из двух этапов. На первом этапе, три комплекта нечетких лингвистических оценок были использованы для теста 100 прогонов. На втором этапе, два набора нечетких лингвистических оценок, которые квалифицированы на стадии 1 использованы в течение 1000 тестовых прогонов. Оценка эффективности предложенной методики была основана на алгоритме FWA и четырех индексах производительности.

Список использованной литературы

1. R. E. Bellman, L. A. Zadeh Decision making in a fuzzy environment, Manage. Sci. 17B, 141-164, 1970.
2. W. J. Kickert Fuzzy Theories on Decision Making: A Critical Review, Martinus Nijhoff, Leiden, Netherlands, 1978.
3. H. J. Zimmermann Fuzzy programming and linear programming with several objective functions, Fuzzy Sets Syst. 1, 45-55, 1978.
4. J. M. Belin Fuzzy relations in group decision theory, J. Cybernet. 4, 17-22, 1974.
5. J. C. Bezdek, B. Spillman, R. Spillman A fuzzy relation space for group decision theory, Fuzzy Sets Syst. 1, 255-268, 1978.
6. J. C. Bezdek, B. Spillman, R. Spillma, Fuzzy relation spaces for group decision theory: an application, Fuzzy Sets Syst. 2, 5-14, 1979.
7. R.R. Yager, Multiple objective decision-making using fuzzy sets, Int. J. Man-Mach. Stud. 9, 375-382, 1977.
8. R.R. Yager, Fuzzy decision making including unequal objectives, Fuzzy Sets Syst. 1, 87-95, 1978.
9. T.L. Saaty, Measuring the fuzziness of sets, J. Cybernet. 4, 53-61, 1974.
10. T.L. Saaty, Exploring the interface between hierarchies, multiple objectives and fuzzy sets, Fuzzy Sets Syst. 1, 57-68, 1978.
11. R.R. Yager, A new methodology for ordinal multiobjective decision based on fuzzy sets, Decis. Sci. 12, 589-600, 1981.
12. S. M. Baas, and H. Kwakernaak, Rating and ranking of multi-aspect alternatives using fuzzy sets, Automatica 13, 47-58, 1977.
13. W.M. Dong, H. C. Shah, F. S. Wong, Fuzzy computations in risk and decision analysis, Civ. Eng..Syst. 2, 201-208, 1985.
14. W.M. Dong, F. S. Wong, Fuzzy weighted averages and implementation of the extension principle, Fuzzy Sets Syst. 21, 183-199, 1987.
15. T.Y. Tseng, and C.M. Klein, A survey and comparative study of ranking procedures in fuzzy decision making, Working Paper No. 8812101, Dept. of Industrial Engineering, Univ. Missouri-Columbia, submitted to Fuzzy Sets Syst. 1989.
16. T.Y. Tseng, and C.M. Klein, A new algorithm for the ranking procedure in fuzzy decision making, IEEE Trans. Syst. Man, Cybern. 19(5), 1289-1296, 1989.