Аннотация
Змея – это сплайн с минимизацией энергии, который руководствуется внешними ограничивающими силами и влиянием сил изображения, которые тянут его к функции, например к линиям и краям. Змеи являются модели активных контуров: они стремятся к близлежащим краям, стремясь точно совпасть с ними. Масштабирование пространства может быть использовано для увеличение области захвата функции выделения. Змеи обеспечивают универсальный способ обнаружения визуальных параметров, в том числе обнаружения краев, линий, контуров и объектов; отслеживание движения; и стерео соответствия. Змеи были успешно использованы для интерактивного пояснения пользователю о введенных ограничений силы направляющих змею по ряду интересующих особенностей.
Общая постановка проблемы
Колебательные процессы в технике имеют большое значение. Электромагнитные колебания лежат в основе всех современных электронных средств передачи и обработки информации.
Для облегчения понимания общих закономерностей колебательных процессов целесообразно начинать их изучение с простых и наглядных систем, например, замкнутая цепь, содержащая конденсатор и катушку индуктивности. Изменение во времени физических величин, характеризующих разные колебательные системы, описывается одинаковыми дифференциальными уравнениями.
Исследование компьютерных программ при моделировании разных способов возбуждения колебаний позволяет определить точностные и частотные характеристики программ.
1. Введение
В недавних исследованиях компьютерного зрения, задачи низким уровня, такие как обнаружение границ или обнаружения линий, стерео обнаружения и отслеживания движения были широко рассматриваемы в качестве автономных, набирающих популярность, исследуемых процессов. Марр и Нишихара [11], в серьезном этой точки зрения заявлении, говорят, что до 2.5D эскиза, информация "сложного уровня" не еще задействована: проведение расчетов используя только то, что доступно в самом изображении. Этот четко последовательный подход может принести с собой распространение ошибок, которые допускаются при низкоуровневых процессах исключающих возможность коррекции. Поэтому накладывает жесткие требования к надежности механизмов низкоуровневые. Как и ранее, но как более простой способ обработки для низкоуровневых процессов, мы предлагаем свой метод, который должен обеспечить наборы альтернативных решений, среди которых могут оказаться и высокоуровневые процессы, вместо отказа от таких методов и уникальных ответов, которые они несут.
В этой статье мы предлагаем использование минимизации энергии в качестве рамок, для реализации этой цели. Мы стремимся разрабатывать энергетические функции, чьи локальные минимумы содержат набор альтернативных решений, доступных для процессов более высокоуровневые. Выбор среди этих альтернатив может потребовать некоторого типа поиска или высокоуровневые мышления. В виду отсутствия хорошо развитых механизмов для высокоуровневых процессов, мы используем интерактивный подход к изучению альтернативному устройству. Посредством добавления соответствующих дополнительных условий к энергии, при стремлении к минимуму, при желании пользователя, для перехода модели от локального минимума к искомому решению. Результатом активной модели, которая получила нужное решение, является решения лежащее вблизи к искомому решению.
Энергетические модели минимизации имеют богатую историю, если оглянуться в прошлое, как минимум стерео модели Сперлинга [16]. Такие модели, как правило, рассматриваются в качестве самостоятельных, но мы разработали интерактивные методы для направления их. Взаимодействие с такими моделями позволяет нам очень легко исследовать энергетическое поле и разработать эффективные функции энергии, которые имеют несколько локальных минимумов и мало зависят от исходных точек. Мы надеемся, таким образом, сделать работа с высоким уровнем интерпретации, ограничившись от излишних низкоуровневых решений.
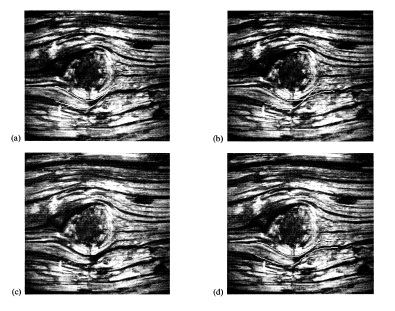
Рисунок 1. Снизу-слева: Оригинал дерева фотография из Brodatz. Остальные: Три различных локальных минимумов для модели активных контуров.
Главная проблема которая рассматривается, заключается в нахождении существенные контуров изображения, их границ, линий и объектов, а так же отслеживание этих контуров при движении и соответствие их стерео изображению. Наш вариационный подход к нахождению контуров изображения отличается от традиционного подхода обнаружения границ, а так же связывает их. В нашей модели присутствуют такие параметры, как определение контуров и наличие способов влиять на функционал энергии и, следовательно, подробную структуру локально оптимального контура. Проблемы такого выделения могут быть решены при помощи высокоуровневых вычислений. Возможно, что еще более важно, высокоуровневые механизмы могут взаимодействовать с моделью контура, толкая его к соответствующим локальным минимумом. Оптимизация обнаружения краевой линии использовалась и ранее [3,5,13,24,25], но без интерактивного направляющей , которая используется здесь.
Во многих задач интерпретации изображения, правильная интерпретация низкоуровневых событий может потребовать знания проблемы на высоком уровне. Рассмотрим, например, три восприятия организации двух темных линий в рисунке 1. Три различные организации соответствуют трем различным локальных минимумам в нашей модели линии контура. Важно заметить, что формы линий существенно отличаются в трех примеров, не только из-за разного связывания отрезков. Сами сегменты изменяются восприятием их организации.
Без детального знания об объекте в целях, трудно оправдать выбор среди трех интерпретаций. Зная, что древесина слоистая структура, или, возможно, делая вывод о ее слоистости, структура из других картинок может помочь исключить интерпретацию (б). Кроме того, задача очень зависит от "правильной" интерпретации. Во многих областях, таких как анализ сейсмических данных, выбор интерпретации может зависеть от специальных знаний. Различные сейсмические интерпретаторы могут иметь существенно отличающиеся восприятия организации о тех же самых сейсмических разрезах в зависимости от их знаний и подготовки. Так как единственная "правильная" интерпретация не всегда может быть определена, то мы предлагаем низкоуровневые механизмы, которые стремятся к соответствующему локальному минимуму, а не ищут глобальный минимум.
В отличие от большинства других методов для нахождения контуров, наша модель является активной. Он всегда стремится к минимуму ее функционала энергии и, следовательно, имеет динамическое поведение. Из-за возможности контура изменяться во время стремления к минимуму его энергии, мы называем его змей. Изменения в высокоуровневых интерпретациях могут оказывать силы действующие на змею, поскольку она продолжает стремиться к их минимизации. Даже при отсутствии таких сил, змеи демонстрируют гистерезис при воздействии движущих стимулов.
Змеи не могут решить все проблемы нахождения соответственных контуров изображения. Они полагаются на иные механизмы обнаружения, чтобы разместиться где-то рядом с нужным контуром. Тем не менее, даже в тех случаях, когда удовлетворительных параметров для автоматической работы механизма обнаружения, змеи могут по-прежнему использоваться для полуавтоматической интерпретации изображений. Если пользователь проложит змею близко к контуру, ее минимизация энергии будет основной задачей ее остального времени работы. Минимизация обеспечивает сильную помочь
для человека, указывая на особенности контура.
Змеи являются примером более общего техничного сопоставления деформируемых моделей к изображению с помощью минимизации энергии. По целям, эта идея похожа на пластичные шаблоны Уидроу [23] Из любой отправной точки, змея деформирует себя в соответствии с ближайшими выступами контура. Мы применили те же основные приемы к проблеме 3D реконструкции объекта из силуэтов с помощью энергии минимизация поверхности с предпочтительными симметриями [17]. Мы ожидаем, что этот общий подход найдет широкий спектр применения в компьютерном зрении.
В разделе 2 мы представляем основное математическое описание змей вместе со своими уравнениями Эйлера. Затем в разделе 3 мы даем подробную информацию о различных энергиях, которые могут влиять на змею, привлекая различные типы важных статических монокулярных функций, таких как линии, края и субъективные контуры. Раздел 4 области применимости моделей змей, стерео обнаружение и отслеживания движения. Наконец, в разделе 5 обсуждаются дальнейшие уточнения и направления нашей текущей работы.
2 Основы поведения змей
Наша базовая модель змеи контролируется непрерывностью [18] сплайна под влиянием сил изображения и внешних ограничительных сил. Внутренние сглаживающие силы служат для наложения ограничения гладкости контура. Сила изображения сдвигает змею к характерных особенностям изображения, как линии, края и прочим особенностям контуров. Внешние ограничивающие силы ответственны за то, что бы змея оставалась змею рядом с нужным локальным минимумом. Эти силы могут, например, поступать из пользовательского интерфейса, автоматических механизмов и высокоуровневых интерпретаций.
Представляя позицию змеи параметрически v(s) = (x(s),y(s)), мы можем описать функционально свою энергию, как
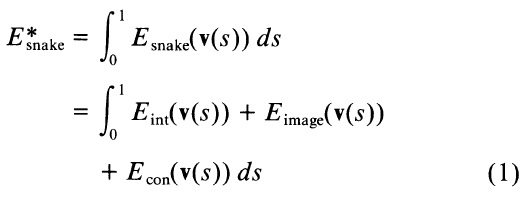
где Eint представляют внутреннюю энергию сплайна вследствие изгиба, Eimage приводит к проявлению сил изображения, и Econ приводит к проявлению внешних ограничений сил. В этом разделе, мы разрабатываем Fint и приведем примеры Econ для интерактивного интерпретации. Eimage будет описана в разделе 3.
2.1 Внутренняя энергия
Внутренняя энергия сплайна может быть записана так:
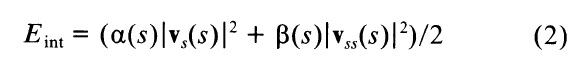
Энергия сплайна состоит из производной первого порядка контролируемой α(s) и в производной второго порядка контролируемой β(s).Производная первого порядка на змею действуют как мембрана, а производная второго порядка действует как тонкая пластина. Регулировка весов α(s) и β(s) контролирует относительную важность влияния мембран и тонких пластин. Стремление β(s) к нулю в точке, позволяет змее стать прерывистой второго порядка и работать навстречу. Контролируется непрерывность сплайна обобщением стабилизатора Тиконове [19] и может быть формально рассмотрено как упорядочивание [14,15] проблем.
Подробная информация о нашей процедуре минимизации приведены в приложении. Процедура O(n) итерационный метод с использованием разреженных матричных методов. Каждая итерация эффективно принимает неявные условия Эйлера к шагам по отношению к внутренней энергии и явные условия Эйлера шаги по отношению к образу и внешней энергии ограничения. В полностью явном метод Эйлера, он принимает O(n2) итерации каждый из O(n) времени импульса, чтобы передвигаться по всей длине змеи. Полученные змеи медленные. Для того, чтобы создать более жестких змей, жизненно важно, чтобы использовался более устойчивый метод, который может вместить большие внутренние затраты. Наша полу-неявный метод позволяет силампередвигаться по всей длине змеи в одину O(n) итерацию.
2.2 Змеиная яма
Для того, чтобы экспериментировать с различными функциями энергии для визуальных низкоуровневых задач, мы разработали пользовательский интерфейс для змей на машине использующий символику Lisp. Интерфейс позволяет пользователю выбрать исходные точки и влиять на змей в интерактивном режиме, во время их минимизации энергии. В дополнение к своей ценности в качестве исследовательского инструмента, пользовательский интерфейс оказался очень полезным для полуавтоматической интерпретации изображений. Для того, чтобы задать конкретный признак изображения, пользователю стоит лишь нажать на змею рядом с функцией. После этого, минимизация энергии будет тянуть змею, приближая ее к остальным отрезкам. Точное отслеживание особенностей контуров может быть более точным, в случае если самостоятельно указывать начальные позиции. Минимизация энергии змей может обеспечить сильную помощь
при интерпретации изображений.
Наш интерфейс позволяет пользователю присоединить силу натяжения к любой точке на змее. Другой конец силы натяжения может быть закреплен в фиксированном положении, соединеняя с другой точкой на змее или перетащить с помощью мыши. Создание силы натяжения между x1 и x2 просто добавляет -k(x1-x2)^2 к внешней энергии ограничения Econ.
В дополнение к источниками, пользовательский интерфейс обеспечивает 1/r2 силу отталкивания, управляемую с помощью мыши. При 1/r функционал энергии обрезается рядом с r = 0 чтобы предотвратить числовую неустойчивость, так в результате потенциал изображен значок вулкана. Вулкан очень полезен для толкания змеи из одного локального минимума и в другой.
Рисунок 2 показывает интерфейс змеиной яма в использовании. Два темные линии различные змеи, которые пользователь связан с двумя источниками, показанными на белом. Остальные источники прилагаются к точкам на змее в фиксированных позициях на экране. В правом верхнем углу вулкан, виден изгиба поблизости него на змее. Каждая из змей имеет острый угол, который был указан пользователем.
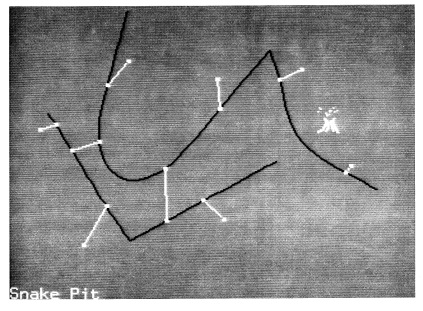
Рисунок 2. Пользовательский интерфейс змеиной ямы. Змеи показаны черным, силы натяжения и вулкан в белым.
3 Силы изображения
Для того, чтобы змеи были полезны для компьютерного выделения, мы должны ввести функционалы энергии, которые определяют характерные черты в образах. В этом разделе мы представляем три различных энергетических функционала, которые стягивают змею к линиям, краям и окончаниям. Полная энергия изображения может быть выражена в виде взвешенной комбинации из трех функционалов энергии путем регулировки весов, что позволит задать широкий диапазон поведения змеи.
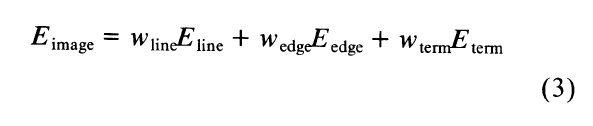
3.1 Линия функционала
Простейшим показателем функционала изображения является функционал интенсивности самого изображения. Если мы положим

то в зависимости от знака wline, змея будет передвигаться либо к светлым линиям или к темным линиям. С учетом других своих ограничений, змея будет пытаться выровнять себя с светлой или темной линий в соседнем контуре. Эта энергия используется в функционале змеи, показанной на рисунке 1. При использовании вулкана, пользователь может быстро переместить змею с одной из этих позиций на другую. Грубая регулировка позволит сделать так, что, предположительно, механизмы обращающие внимание на символическое описание, могли бы эффективно управлять змеей.
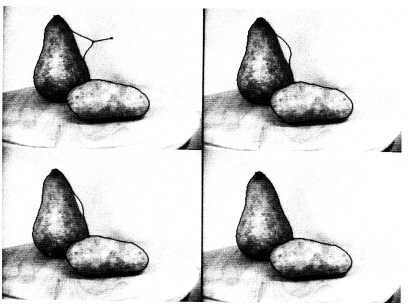
Изображение 3. Два края змеи на груше и картофеле. Верхний левый: Пользователь вытащил одну из змей вдали от края груши. Остальные: После того как пользователь отпускает, змея перемещается назад к краю груши.
3.2 Функционал границ
Нахождение границ в изображении может быть сделано с очень простой функционалом энергии. Если мы положим Fedge = -|▼I(x,y)|2, то змея будет продвигаться к контурам с большими градиентами изображения. Пример использования этого функционала показано на рисунке 3. В левом верхнем углу, пользователь разместил две змеи по краям груши и картофель. Затем он вытащил часть змеи от груши силой натяжения. Остальные фотографии показывают, что происходит, когда он отпускает. Змея быстро встанет обратно к границе груши.
3.3 Масштабируемое пространство
На рисунке 3, змея притягивается к границе груши с достаточно большого расстояния, из-за влияния энергии сплайна. Этот тип конвергенции довольно часто используем для змей. Если часть змеи находит функцию изображения с низкой энергией, сплайн будет тянуть соседние части змеи в сторону возможного продолжения функции. Это эффективно размещает большую часть энергии вокруг хорошего локального минимума. Аналогичный эффект может быть достигнут с помощью пространственно сглаживания граничного или линейного функционала энергии. Можно позволить змее прийти к равновесию на очень размытом функционале энергии, а затем медленно снизить размытость. Результатом является минимизация при помощи масштабирования [20,21]
Для того, чтобы показать взаимосвязь масштабируемого пространства в теории Марра-Хилдрета обнаружения границ [10], мы экспериментировали с несколько иными краевыми функционалами. Краевой-функционал энергии
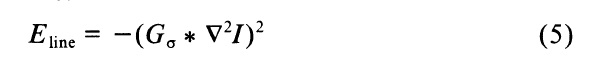
где Gσ это гауссовский стандарт отклонения, а минимумы этого функционала лежат на нулевых пересечениях Gσ*▼^2*I определяющих границы в теории Марра-Хилдрета. Добавление этого термина энергии в змею означает, что змею привлекает нулевые-переходы, но она по-прежнему придерживается своей гладкости. Рисунок 4 показывает масштабируемое пространство применительно к этому функционалу энергии. Верхний- левый показывает змею в равновесии при очень грубой шкале. Если функцией краевой энергии очень размыты, змея выполняет очень плохую работу при локализации края, но приближается к этому локального минимума с больших расстояний. Медленное уменьшение размытия приводит змею в положение, показанное в верхнем правом углу и, наконец, в положение, показанное в нижнем левом углу. Для справки, нулевые-переходы Gσ*▼^2*I соответствующая функции энергии змеи в левом нижнем углу показаны накладывается на той же змея в нижний правый. Обратите внимание, что змея прыгает из одного куска нулевого пересечения контура к другому. В этом масштабе, формы нулевых пересечений доминирует малые текстуры, а не границы области, но, тем не менее змея может использовать нулевой пересечения для локализации из-за его ограничения гладкости.
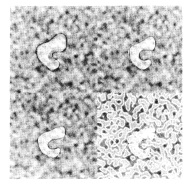
Рисунок 4. Сверху-слева: границы змеи в равновесии при грубой шкале. Сверху-справа: змея в равновесии при промежуточном масштабе. Снизу-слева: итоговая змея в равновесии при шкале масштабирования. Справа-снизу: нулевые-переходы накладывается на конечные позиции змеи.
3.4 Остановка функционала
Для того чтобы найти окончания отрезков и углов, мы используем кривизну линий уровня в нескольких сглаженных изображениях.
Пусть C(x,y) = Gσ(x,y)*I(x,y) будет слегка сглаженным изображением. Пусть θ = tan-1(Cy/Cx) быть углом градиента и пусть n = (cos θ, sin θ) и n = (-sin θ, cos θ) единичные векторы продольные и перпендикулярные к направлению градиента. Тогда кривизна контуров в C(x,y) может считаться
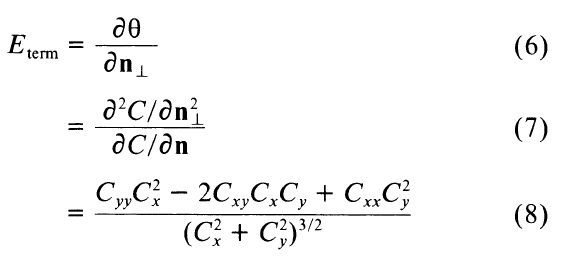
Комбинируя Eedge и Eitem, мы можем создать змею, которая притягивается к краям или окончаниям. На рисунке 5 показан пример того, как змеи воздействуют к стандартным параметрам предполагаемых контуров [7]. Форма змеи контура между краями и линий в иллюзии полностью определяется сроком сплайн гладкости. Вариационная задача, решаемая с помощью змеи, очень тесно связана с вариационной формулировкой, предложенной Брэди и др. [2] для интерполяции субъективных контуров. Ульман [22] предложил интерполяция, используя кусочно-круговые дуги, вероятно, так же производят очень похожие интерполяции. Привлекательным аспектом модели является то, что змеи змея же, что находит субъективные контуры, может очень эффективно найти более традиционные ребра естественного изображения. Это может случаться потому, что обеспечивается некоторое понимание, что способность видеть субъективные контуры – важна.
Далее необычный аспект змеиных моделей, носящей в психофизике субъективных контуров название гистерезис. Так змеи постоянно минимизации их энергию, они могут проявлять гистерезис, когда показано перемещение раздражителей. Рисунок 6 показывает змею отслеживающую движущийся контур. Как горизонтальный отрезок смещается направо, змея изгибается больше и больше, пока внутренние сглаживающие силы не уравновесят силы изображения. Тогда змея отпускает линию и возвращается к гладкой форме. Приведение сегмента достаточно близко к змее крепит ее к себе. Хотя это трудно показать гистерезис неподвижного изображения, читатель может легко проверить, соответствующий гистерезис человеческого зрения, используя движущийся раздражитель. Этот тип гистерезиса нехарактерен в основном для процессов идущих по нарастанию и глобальных оптимизаций.

Рисунок 5. Справа: стандартный пример контура. Слева: граница/прекращение движения змеи из-за позиции равновесия.

Рисунок 6. Сверху-слева: динамический пример контура. Последовательно слева направо, сверху вниз. Сверху-справа: змея стремится к границам и окончаний. Так как движется горизонтальная линия, скользя вправо, змея изгибается, пока она не падает линии. Приведение линии достаточно близко прикрепляет змею.
4 Стерео и движения
4.1 Стерео
Змеи могут быть применены к проблеме стереоскопического сравнения. В стерео, если два контура соответствуют, то неравенство медленно изменяются вдоль контура, если контур быстро не отступает в глубину. Психофизически свидетельствует [4] предел разрыва градиента человеческого восприятия стереоскопического указывает, что зрительная система человека, по крайней мере до некоторой степени предполагает, что различия в пространстве не изменяются слишком быстро. Это ограничение может быть выражено в качестве дополнительного функционала энергии для стерео змеи:
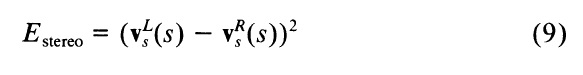
где vL(s) и vR(s) левый и правый контуры змеи, соответственно.
Несоответствие гладкости ограничения применяется наряду контуров, он разделяет сильное сходство с [8] гладкостью ограничения Хилдрет для вычисления оптического потока. Это ограничение означает, что в процессе локализации контура в одном глазу, информация о соответствующем контуре в другом глазу так же используется. В стерео змеях, стерео пара на самом деле влияет на обнаружение и локализацию функций, на которых основывается пара. Это отличие важно, например, из стерео-теории Марра-Поджо [12], в которой основным стереоскопическое сравнение примитивные нулевых пересечений всегда остаются неизменными в процессе подбора.
Рисунок 7 показывает пример 3D поверхности, восстановленной из неравенства измеряемых по одной стерео змей на контур куска бумаги. Поверхность показана совсем с другой точки зрения, чем оригинал, чтобы подчеркнуть, что 3D-модель бумажке была вычислена, а не просто является моделью 2.5D.
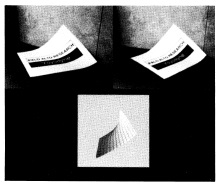
Рисунок 7. Сверху: Стереограмма изогнутого листа бумаги. Внизу: реконструкция поверхности по контуру бумаги согласованного с помощью стерео змей. Модель поверхности показана совсем с другой точки зрения, чем оригинал, чтобы подчеркнуть, что это полное 3D модель, а не модель 2.5D.
4.2 Движение
После того, как змея находит заметную визуальный функцию, она фиксирует ее. Если функция начинает медленно смещаться, змея будет просто отслеживать тот же локальный минимум. Быстрое движение может не вызвать реакцию змеи, чтобы переместить ее в другой локального минимума, а при обычных скоростях и отбора проб видео, змеи выполняют хорошую работу отслеживания движения. Рисунок 8 показывает восемь выбранных кадров из последовательности двух секунд видео. Краевые привлеченных змеи были инициализированы вручную на губах говорящего в первом кадре. После этого, змеи отслеживали движения губ автоматически.
Отслеживание движения было сделано в данном случае без каких-либо ограничений межкадровых. Введение таких ограничений будет несомненно сделать отслеживания более надежной.Самый простой способ сделать так, чтобы дать массу змея. Тогда змея предсказать его следующую позицию на основе своего предыдущего скорости.
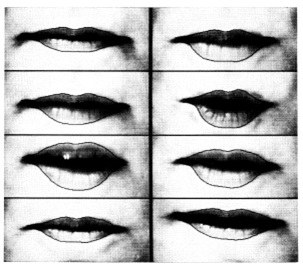
Рисунок 8. Отдельные кадры из 2-второй видеопоследовательности, показывая змей, используемые для отслеживания движения. После инициализации к губам говорящего с в первом кадре, змеи автоматически отслеживать движения губ с высокой точностью.
5. Заключение
Змеи оказались полезными для интерактивной спецификации контуров на изображении. Мы начали использовать их в качестве основы для интерактивного соответствие 3D-моделей с изображениями. При хорошем развитии функционалов энергии, хорошая помочь
змей становится все более эффективной. Масштабируемое пространство может значительно увеличить область захвата вокруг интересующих областей изображения.
Змеиные модели обеспечивают универсальный способ решения визуальных проблем, по разному решаемых в прошлом. Границы, линии, контуры и объекты могут быть найдены по одним и тем же механизмам обнаружения. Отслеживание движения и сопоставления их в стерео легко обрабатываются в тех же рамках.
Змеи, возможно, воплотить идею Марра о наименьшей зависимости
[9] больше, чем его 2.5D эскизы. Змея предоставляет ряд широко разделенных локальных минимумов в дальнейших уровнях обработки. Вместо того, чтобы совершить безвозвратные интерпретации, змеи могут изменить свою интерпретацию на основе дополнительных доказательств от высокоуровневой обработки. Они могут, например, регулировать монокуляр краевого-вывода на основе бинокулярных пар.
Мы считаем, что способность иметь все уровни визуального воздействия обработки визуальных интерпретаций, начиная с самого низкоуровневого, является очень важным. Местные энергетические системы минимизации, как змеи, предлагают привлекательный способ сделать это. Минимизация энергии приводит к гораздо более простой задаче обработки с более высокоуровневой обработкой.
Благодарности
Курт Флейшер сильно помог с змеиными сплайнами в пользовательском интерфейсе и создал все важные параметры вулкана. Джон Платт помог нам разработать теорию змеи и вел нас вокруг бесконечной бездны численных методов. Змея-губы Аткинсона – основные условия визуальных стимулов движения.
Приложение: Численные методы
Пусть Eext = Eimage + Econ. Когда α(s) = α, и β(s) = β являются константами, минимизации функционала энергии уравнения (1) приводит к следующим двум независимым уравнениям Эйлера:
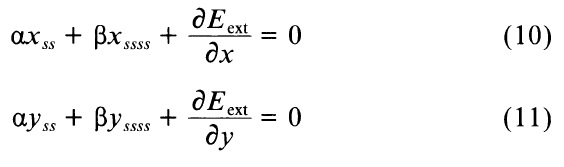
При α(s) и β(s) не являющихся постоянными, точнее, при переходе непосредственно к дискретной формулировке функционала энергии в уравнении (2). Тогда мы можем написать:
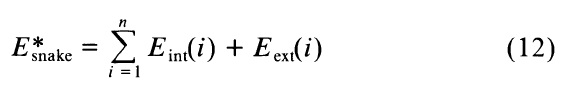
Приближение производных с конечными разностями и преобразования в векторной форме с vi = (xi,yi) = (x(ih),y(ih)) мы разлагаем Eint(i):
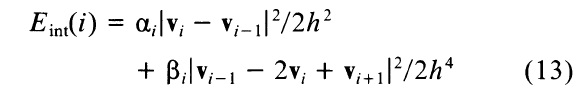
где мы определяем что v(0) = y(n). Пусть fx(i) = ∂Eext/∂xi и fy(i) = ∂Еext/∂yi где производные аппроксимируется конечной разности, если они не могут быть вычислены аналитически. Теперь соответствующие уравнения Эйлера:
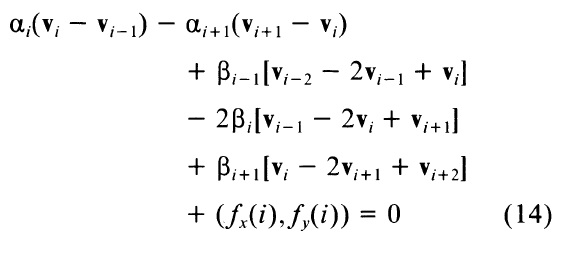
Вышеприведенные уравнения Эйлера можно записать в матричной форме как:

где A пентадиагональная объединенная матрица.
Для решения уравнений (15) и (16), мы устанавливаем правые части уравнений, равными произведению размера шага и негативных производных по времени левых сторон. Принимая во внимание производные внешних сил, которые мы используем требуется изменение A на каждой итерации, таким образом, мы можем достичь более быстрых итераций просто предполагая, что fx и fy постоянны в течение временного шага. Это дает явный метод Эйлера по отношению к внешним силам. Внутренние силы, однако, полностью определяется полосчатой матрицей, таким образом, мы можем оценить производную по времени в момент времени t чем время t - 1 и, следовательно, прийти к неявным шагам Эйлера для внутренних сил. Полученные уравнения:
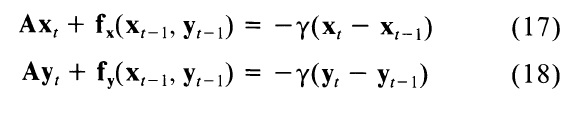
где Y представляет собой размер шага. В равновесии, производная по времени равна нулю, и мы в конечном итоге с решением уравнений (15) и (16).
Уравнения (17) и (18) могут быть решены с помощью обращения матрицы:
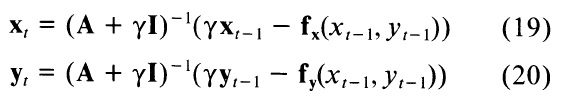
Матрица A + γI это пентагональные диапазоны матрицы, так что его инвертирование может быть вычислено путем LU-разложения в O(n) время [6,1]. Следовательно уравнения (19) и (20) обеспечивают быстрое решение уравнений (15) и (16). Способ применяется по отношению к внутренним силам, так что он может вычислить очень жестких змей с шагами большого размера. При увеличении воздействия внешних сил, явные методы Эйлера на этапы внешних сил потребуют значительно меньших размеров шага.
Список использованной литературы
1. A Benson, and DJ. Evans, ACM TRANS. MATHE-MATICAL SOFTWARE, vol. 3, pp. 96-103, 1977.
2. M. Brady, W.E.L. Grimson, and D. Langridge, “Shape en-coding and subjective contours,” PROC. AM. ASSOC. ARTIF. INTEL., Stanford University, 1980.
3. D.J. Burr, “Elastic matching of line drawings,” IEEE TRANS. PAMI-8, p. 708, 1986.
4. P. Burt, and B. Julesz, “A disparity gradient limit for binocular fusion,” SCIENCE, vol. 208, pp. 615-617,1980.
5. M.A Fischler, and R.A Elschlager, “The representation and matching of pictorial structure,” IEEE TRANS. ON COMPUTERS, vol. C-22, pp. 67-92, 1973.
6. I. Gladwell, and R. Wait (eds.), A SURVEY OF NU-MERICAL METHODS FOR PARTIAL DIFFERENTIAL EQUATIONS. Clarendon: Oxford, 1979.
7. Kanisza, “Subjective contours,” SCIENTIFIC AMERICAN, vol. 234, pp. 48-52, 1976.
8. E. Hildreth, “The computation of the velocity field,” PROC. ROY. SOC. (LONDON), vol. B221, pp. 189-220.
9. D. Marr, VISION. Freeman: San Francisco, 1982.
10. D. Marr and E. Hildreth, “A theory of edge detection,” PROC. ROY. SOC. (LONDON), vol. B207, pp. 187-217, 1980.
11. D. Marr and H.K Nishihara, “Visual information pro-cessing: Artificial Intelligence and the sensorium of sight,” TECHNOLOGY REVIEW, vol. 81(1), October 1978.
12. D. Marr and T. Poggio, “A computational theory of human stereo vision,” PROC. ROY. SOC. (LONDON), vol. B204, pp. 301-328, 1979.
13. A. Martelli, “An application of heuristic search methods to edge and contour detection,” CACM, vol. 19, p. 73, 1976.
14. T. Poggio and V. Toree, “Ill-posed problems and regulari-zation analysis in early vision,” PROC. AARPA Image Understanding Workshop, New Orleans, L.A, Baumann (ed.), pp. 257-263, 1984.
15. T. Poggio, V. Toree, and C. Koch, “Computational vision and regularization theory,” NATURE, vol. 317(6035), pp. 314-319, 1985.
16. G. Sperling, “Binocular vision: a physical and a neural theory,” AM. J. PSYCHOLOGY, vol. 83, pp. 461-534, 1970.
17. D. Terzopoulos, A. Witkin, and M. Kass, “Symmetry- seeking models for 3D object reconstruction,” INT. J. COMPUTER VISION, vol. 3, 1987.
18. D. Terzopoulos, “Regularization of inverse visual problems involving discontinuities,” IEEE TRANS. PAMI-8, p. 413, 1986.
19. AN. Tikhonov, “Regularization of incorrectly posed problems,” SOV. MATH. DOKL., vol. 4, pp. 1624-1627, 1963.
20. A Witkin, “Scale space filtering,” PROC. EIGHTH INT. JOINT CONF. ARTIF. INTEL., Karlsruhe, pp. 1019- 1021, 1983.
21. A Witkin, D. Terzopoulos, and M. Kass, “Signal matching through scale space,” PROC. AM. ASSOC. ARTIF. INTEL., Philadelphia, pp. 714-719, 1986.
22. S. Ullman, “Filling the gaps: The shape of subjective con-tours and a model for their generation,” BIOLOGICAL CYBERNETICS, vol. 25, 1976.
23. B. Widrow, “The rubber mask technique, parts I and II,” PATTERN RECOGNITION, vol. 5, pp. 175-211, 1973.
24. S. Zucker, R. Hummel, and A. Rosenfeld, “An application of relaxation labeling to line and curve enhancement,” IEEE TRANS. ON COMPUTERS, vol. C-26, p. 394, 1977.
25. S. Zucker, “Computational and psychophysical experiments in grouping: Early orientation selection.” In HUMAN AND MACHINE VISION, Jacob Beck, et al. (eds.), Academic Press: New York, pp. 545-567, 1983.