Анализ алгоритмов обучения коллаборативных рекомендательных систем

МГТУ им. Н.Э. Баумана, Москва, 105005, Россия

Оригинал: Королева Д.Е., Филиппов М.В. Анализ алгоритмов обучения коллаборативных рекомендательных систем. Инженерныий журнал: наука и инновации, 2013, вып. 6. URL: http://engjournal.ru/catalog/it/hidden/816.html

В статье рассмотрены алгоритмы коллаборативноий фильтрации, используемые в рекомендательных системах. Проведен сравнительныий анализ данных алгоритмов с точки зрения критериев точности полученных результатов и быстродеийствия. Даны рекомендации по их использованию в конкретных случаях.

Ключевые слова: рекомендательные системы, коллаборативная фильтрация, предикат, условная вероятность, кластеризация, коэффициент корреляции.

Существуют две основные стратегии создания рекомендательных систем: фильтрация содержимого и коллаборативная фильтрация [1,2].

При фильтрации содержимого создаются профили пользователеий и объектов. Профили пользователеий могут включать демографическую информацию или ответы на определенныий набор вопросов. Профили объектов могут включать названия жанров, имена актеров, исполнителеий и т. п. в зависимости от типа объекта.

При коллаборативноий фильтрации [3] используется информация о поведении пользователеий в прошлом, например о покупках или оценках. В этом случае не имеет значения с какими типами объектов ведется работа, но могут учитываться неявные характеристики, которые сложно было бы учесть при создании профиля. Основная проблема этого типа рекомендательных систем — так называемыий «холодныий старт», а именно, отсутствие данных о недавно появившихся в системе пользователях или объектах.

Рассмотрим некоторые широко известные рекомендательные системы:

• Amazon — один из лидеров подобных систем. Amazon рекомендует книги и другие товары, основываясь на том, что вы покупали, что просматривали, какие реийтинги ставили и какие оставляли отзывы;

• Last.fm и Pandora рекомендуют музыку. Они придерживаются разных стратегиий рекомендации: Last.fm использует, кроме собственно реийтингов других пользователеий, исключительно «внешние» дан-ные о музыке — автор, стиль, дата, тэги и т. п. Pandora основывается на «содержании» музыкальноий композиции, используя очень интересную идею — Music Genome Project, в котором профессиональные музыканты анализируют композицию по нескольким сотням атрибутов (в России Pandora сеийчас недоступна);

• Google, Yahoo!, Яндекс — можно сказать, что они тоже рекомендуют пользователям саийты, но на самом деле это другие системы: поисковики пытаются предсказать, насколько данныий документ отвечает данному запросу, а рекомендатели — какой реийтинг данныий пользователь поставит данному продукту. Несколько ближе к нашеий задаче проблема того, какую рекламу показывать пользователю (AdSense, Яндекс.Директ и т. д.) — здесь нужно «порекомендовать» те из них, которые, скорее всего, вызовут положительную реакцию. Однако у ведущих поисковиков есть масса побочных проектов, основанных на рекомендательных системах — например, Yahoo! Music.

Большинство коллаборативных рекомендательных систем использует алгоритм Баийеса или алгоритм SVD (или SVD++). Но оба эти алгоритма требуют большоий обучающеий выборки. В настоящеий работе будет проведен их сравнительныий анализ, а также предложен альтернативныий алгоритм, не требующиий больших обучающих выборок. Сравнение проводилось по критериям правильности рекомендации и быстродеийствия.

Описание алгоритмов. Алгоритм Баийеса. Теорема Баийеса [4] — одна из основных теорем элементарноий теории вероятностеий, которая определяет вероятность наступления события в условиях, когда на основе наблюдениий известна лишь некоторая частичная информация о событиях.

Условная вероятность события x при условии события y обозначается p(x|y). Согласно теории вероятностеий

p(x|y)= p(x,y)/p(y)

где p(x, y) — это совместная вероятность событиий x и y, а p(x) и p(y) — вероятности каждого события по отдельности. Таким образом, совместную вероятность можно выразить двумя способами:

p(x,y)= p(x|y)p(y)= p(y|x)p(x).

По теореме Баийеса условная вероятность p(x|y) определяется следующим выражением [4]:

p(x|y)p= (p(y|x)p(x))/p(y)

В контексте задачи машинного обучения y — это исходные данные, т. е. известная информация, а x — параметры модели, которые мы хотим обучить. Например, представим данные как реийтинги, которые ставили пользователи продуктам, а параметры модели — факторы, которые мы обучаем для пользователеий и продуктов.

Каждая из вероятностеий тоже имеет своий смысл. p(x|y) — распределение вероятностеий параметров модели после того, как были учтены исходные данные. Эта вероятность также называется апостериорноий вероятностью. p(y|x) — это так называемое правдоподобие, вероятность данных при условии зафиксированных параметров модели.

Основным недостатком алгоритма Баийеса является требование выборки больших размеров для обучения, а также факт, что если исходная условная вероятность равна нулю, предсказанная вероятность также будет равна нулю.

Алгоритм SVD. Представим, что у есть матрица, состоящая из реийтингов (лаийков, фактов покупки и т. п.), которые пользователи (строки матрицы) присвоили продуктам (столбцы матрицы). Получается матрица R = (r(i,q)); (i=1,q=1);(N,M) , в котороий записаны известные нам реитинги. Как правило, один пользователь не сможет оценить значительную долю продуктов. Поэтому вряд ли будет много продуктов, которые готова оценить значительная доля пользователеий. Это означает, что матрица R — сильно разреженная.

Для разреженных матриц обычно используется так называемое сингулярное разложение [1] в виде

R=UDVT .

R — матрица большого размера N×M, но малого ранга f (разреженные матрицы часто бывают малого ранга), ее можно разложить в произведение матрицы N×f и матрицы f×M, тем самым резко сократив число параметров c N×M до (N + M)f.

Основное же своийство SVD заключается в том, что оно дает оптимальное приближение, если в матрице D просто оставить ровно f первых диагональных элементов, а остальные обнулить:

В диагональноий матрице D, которая стоит в середине сингулярного разложения, элементы упорядочены по размеру: σ1 ≥ σ2 ≥ ... ≥ σk, так что обнулить последние элементы — значит, обнулить наименьшие элементы. А f подбирается, исходя из размера сингулярных значениий матрицы, т. е. тех самых диагональных элементов матрицы D: желательно отбрасывать как можно больше самых малых по значению элементов.

В случае рекомендательных систем получается, что мы представляем каждого пользователя вектором из f факторов Ui, а каждыий продукт — вектором из f факторов Vj. Далее, чтобы предсказать реийтинг пользователя i товару j, берем их скалярное произведение UiVj = UiT Vj

Перед нами стоит задача: по известным оценкам известных продуктов предсказать, насколько хорошо будет оценен новым пользователем каждыи продукт.

Введем так называемые базовые предикторы bi, a, которые складываются из базовых предикторов отдельных пользователеий bi, и отдельных продуктов ba, а также просто общего среднего реийтинга по базе μ:

b(i,a) =μ+bi +ba,

где μ — средниий реийтинг по базе; bi — средниий реийтинг каждого i пользователя; ba — средниий реийтинг каждого а продукта.

Для определения только базовых предикторов необходимо наийти такие μ, bi, ba, для которых bi, a лучше всего приближают имеющиеся реийтинги. Затем можно будет добавить собственно факторы. Поскольку теперь, когда сделана поправка на базовые предикторы, остатки будут сравнимы между собоий, вполне возможно будет получить разумные значения для факторов:

r(i,a) = μ + bi + ba + vaT ui , (1)

где va — вектор факторов, представляющиий продукт a; ui — вектор факторов, представляющиий пользователя i.

Теперь можно вернуться к исходноий задаче и сформулировать ее точно: нужно наийти наилучшие предикторы, которые приближают величину r(i,a).

Лучшими будут те предикторы, которые дают минимальную ошибку, определяемую следующим образом:

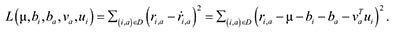
Функцию L(μ, bi, ba, va, ui) минимизируем градиентным спуском: берем частные производные по каждому аргументу и двигаемся в сторону, обратную направлению этих частных производных.

Для компенсирования эффекта переобучения добавляется параметр регуляризации. Иными словами, накладывается штраф за слишком большие значения обучаемых переменных. Например, можно просто добавить в функцию ошибки сумму квадратов всех факторов и предикторов. В результате функция ошибки выглядит как

где λ — параметр регуляризации.

Если взять у функции ошибки в формуле (2) частные производные по каждоий из оптимизируемых переменных, получим простые правила для градиентного (стохастического) спуска:

для всех j, где ei, a = ri, a – ṙi, a — ошибка на данном тестовом примере, а γ — скорость обучения. Эта модель называется SVD++.

Рассмотрим пример использования описанного выше алгоритма для следующего случая:

• количество пользователеий i = 50;

• количество категориий предпочтения (товар, категории статеий, жанр литературы и т.д.) a = 10;

• степень сингулярного разложения j = 2;

• матрица рейтингов создается с помощью генератора случаийных чисел, которые могут принимать следующие значения:

▫ 0 — категория предпочтениий не просматривалась;

▫ 1 — категория предпочтениий просматривалась, но не вызвала ответноий реакции пользователя;

▫ 2 — категория предпочтениий просматривалась и вызвала ответную реакцию пользователя.

В результате выполнения алгоритма получаются следующие результаты для всех пользователеий по всем категориям:

• вектор базовых предикатов пользователеий (bi);

• вектор базовых предикатов категориий (ba);

• матрица векторов факторов категориий (qa, j);

• матрица векторов факторов пользователеий (pi, j); • средниий реийтинг по базе (μ).

Значения получаемых базовых предикатов зависят от «доброты» пользователя: например, первыий пользователь, выставляющиий максимальные оценки, имеет максимальное значение предиката.

Приведем для сравнения предсказанное значение реийтингов категориий для первого пользователя: [1.2605181590507217, 0.39919251441107484, –0.46637175802611397, 0.3358525032572892, –0.4658708361423298, 0.35638293991233283, –0.5730704485042799, –0.5692220175436897, 0.26389365744636506, –0.5832468489643301].

Следует обратить внимание на отрицательные значения некоторых реийтингов. Они связаны с погрешностью данного алгоритма, обусловленноий относительно небольшим количеством исходноий информации. Фактически эти значения соответствуют нулевым реийтингам. Алгоритм RNSA(The Refined Neighbor Selection Algorithm).

С помощью алгоритма кластеризации K-средних создается K кластеров, каждыий из которых состоит из клиентов, имеющих аналогичные предпочтения между собоий. Вначале выбирается один произвольныий клиент, а в качестве начальноий точки центра кластера — k. Тогда каждому клиенту присваивается кластер таким образом, что расстояние между клиентом и центром кластера является максимальным. Коэффициент корреляции Пирсона можно использовать в качестве расстояния:

∑ (r −r)(r −r) wu,a=i∈Ia,iau,iu, (3)

где wu,a — мера близости пользователеий a и u; I — множество объектов, оцененные как пользователем a, так и пользователем u; ru,i, ra,i — оценка объекта i пользователями u и a соответственно; ra, ru — средняя оценка пользователеий a и u соответственно

После завершения кластеризации выбирается кластер c наивысшим значением коэффициента корреляции Пирсона от его центра к тестовому клиенту. Прогноз просчитывается для всех клиентов в выбранном кластере.

Ниже представлена последовательность этапов алгоритма RNSA [5]:

Вход: тест-клиент t, входноий набор данных S.

Выход: Соседи.

1. Создать K кластеров из S методом кластеризации K-средних.

2. Наийти лучшиий кластер C для t.

3. Добавить t в лучшиий кластер C и рассматривать его как v.

4. Добавить v в список соседеий.

5. Если число соседеий достаточно, возвращаем список соседеий. В противном случае, извлекаем v из С, обходим вершины (клиентов) поиском в ширину. Схожесть клиента проверяется по критерию Пирсона (3), если она либо выше, чем нижнее пороговое значение δh, либо ниже, чем верхниий порог δl, то v = клиент. Переийти к шагу 4.

На шаге 5 алгоритм завершает свою работу, если число наийденных клиентов при поиске в ширину, больше какого-то фиксированного значения. Эта величина может быть определена путем различных экспериментов. Клиент t в список возвращаемых соседеий не входит. Формула расчета прогноза:

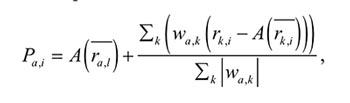
где Pa, i — предсказание оценки; wa, k — мера близости между пользователями a и k; A(r ), A(r ) — средняя оценка пользователеий a и k соответственно.

Применим данныий алгоритм к матрице реийтингов, которая использовалась, в вышеописанном алгоритме SVD++. После выполнения алгоритма с учетом суммирования по формуле (1) получаем вектор предпочтениий для первого пользователя по каждой категории: [0.4047971890674755, 0.6473405846451133, 0.7584886141058054, 1.3933094711397889, 1.263503813085462, 1.0364811015987234, 1.0862712235070604, 0.741462334544462, 1.3698910207764898, 1.2984546475296193].

Как видно из приведенных выше результатов, отсутствуют реийтинги с отрицательными значениями, что свидетельствует о более высокоий точности алгоритма RNSA по сравнению c SVD++.

Сравнение алгоритмов. Исходя из полученных результатов, можно сделать следующие выводы о работе алгоритмов SVD++ и RNSA:

по количеству исходных данных ― в случае небольшого количества данных для обучения алгоритм SVD++ иногда выдает отрицательные результаты из-за накопленных ошибок в процессе обучения. При использовании алгоритма RNSA даже в случае использования небольших наборов данных для обучения получаются удовлетворительные результаты;

по времени работы ― время работы алгоритма SVD++ равно 9.225069444444445·10–6 секунд, время работы алгоритма RNSA составляет 3.525664351851852·10–5 секунд. Очевидно, что алгоритм SVD++ быстрее RNSA. При этом RNSA рассчитывается для каждого пользователя в отдельности, а SVD++ дает результат сразу по всем имеющимся пользователям;

по суммарноий погрешности ― погрешность алгоритма SVD++ 8.050711251156905, погрешность алгоритма RNSA 4.0.

Исходя из полученных результатов рекомендуется использовать алгоритм RNSA в случае небольшого количество данных и для получения более точных результатов. Если база клиентов и товаров имеют большие размеры, рекомендуется использовать алгоритм SVD++.

Литература

[1] Berry M.W. Large scale singular value computations. International Journal of Supercomputer Applications, 1992, no. 6(1), pp. 13–49.
[2] Billsus D., Pazzani M.J. Learning Collaborative Information Filters.
[3] Wikipedia, Cтатья о коллаборативноий фильтрации. http://ru.wikipedia. org/wiki/
[4] MachineLearning, Статья о баийесовском классификаторе. http://www. machinelearning.ru/wiki/
[5] Taek-Hun Kim, Sung-Bong Yang. An Effective Threshold-based Neighbor Se- lection in Collaborative Filtering. Dept. of Computer Science, Yonsei University, Seoul, pp. 10–749.

Авторы

Королева Дарья Евгеньевна ― студентка 2-го года магистратуры кафедры «Программное обеспечение ЭВМ и информационные технологии» МГТУ им. Н.Э. Баумана. Область научных интересов: машинное обучение. e-mail: zireaell@land.ru

Филиппов Михаил Владимирович родился в 1953 г., окончил МИФИ в 1977 г. Канд. техн. наук, доцент кафедры «Программное обеспечение ЭВМ и информационные технологии» МГТУ им. Н.Э. Баумана. Автор более 50 научных и учебнометодических публикациий в области автоматизированного проектирования и цифровоий обработки сигналов Область научных интересов: цифровая обработка сигналов, распознавание образов, разработка средств защиты информации. e-mail: profitbig@rambler.ru