PREA: Personalized Recommendation Algorithms Toolkit
Joonseok Lee, Mingxuan Sun, Guy Lebanon
College of Computing Georgia Institute of Technology Atlanta, Georgia 30332, USA
Editor: Soeren Sonnenburg
Original: http://www.jmlr.org/papers/volume13/lee12b/lee12b.pdf
Abstract
Recommendation systems are important business applications with significant economic impact. In recent years, a large number of algorithms have been proposed for recommendation systems. In this paper, we describe an open-source toolkit implementing many recommendation algorithms as well as popular evaluation metrics. In contrast to other packages, our toolkit implements recent state-of-the-art algorithms as well as most classic algorithms.
Keywords: recommendersystems,collaborativefiltering,evaluationmetrics
Keywords: Personalized Service, Information Retrieve, Information Filtering, Recommender System, Content-Based Filtering, User Interest Model
1. Introduction
As the demand for personalized services in E-commerce increases, recommendation systems are emerging as an important business application. Amazon.com, for example, provides personalized product recommendations based on previous purchases. Other examples include music recommen- dations in pandora.com, movie recommendations in netflix.com, and friend recommendations in facebook.com.
A wide variety of algorithms have been proposed by the research community for recommen- dation systems. Unlike classification where comprehensive packages are available, existing recom- mendation systems toolkits lag behind. They concentrate on implementing traditional algorithms rather than the rapidly evolving state-of-the-art. Implementations of modern algorithms are scat- tered over different sources which makes it hard to have a fair and comprehensive comparison.
In this paper we describe a new toolkit PREA (Personalized Recommendation Algorithms Toolkit), implementing a wide variety of recommendation systems algorithms. PREA offers imple- mentation of modern state-of-the-art recommendation algorithms as well as most traditional ones. In addition, it provides many popular evaluation methods and data sets. As a result, it can be used to conduct fair and comprehensive comparisons between different recommendation algorithms. The implemented evaluation routines, data sets, and the open-source nature of PREA makes it easy for third parties to contribute additional implementations.
Not surprisingly, the performance of recommendation algorithms depends on the data charac- teristics. (Lee et al., 2012a,b) For example, some algorithms may work better or worse depending on the amount of missing data (sparsity), distribution of ratings, and the number of users and items. It is likely that an algorithm may perform better on one data set and worse on another. Furthermore, the different evaluation methods that have been proposed in the literature may have conflicting orderings over algorithms (Gunawardana and Shani, 2009). PREA’s ability to compare different algorithms using a variety of evaluation metrics may clarify which algorithms perform better under what circumstance.
2. Implementation
PREA is a multi-platform Java Software (version 1.6 or higher required). It is compatible with MS Windows, Linux, and Mac OS. The toolkit consists of three groups of classes, as shown in Figure 1. The top-level routines of the toolkit may be directly called from other programming environments like Matlab. The top two groups implement basic data structures and recommendation algorithms. The third group (bottom) implements evaluation metrics, statistical distributions, and other utility functions.

Figure 1: Class Structure of PREA
2.1 Input Data File Format
As in the WEKA1 toolkit PREA accepts the data in ARFF2 (Attribute-Relation File Format). Since virtually all recommendation systems data sets are sparse, PREA implements sparse (rather than dense) ARFF format.
2.2 Evaluation Framework
For ease of comparison, PREA provides the following unified interface for running the different recommendation algorithms.
• Instantiate a class instance according to the type of the recommendation algorithm.
• Build a model based on the specified algorithm and a training set.
• Given a test set, predict user ratings over unseen items.
• Given the above prediction and held-out ground truth ratings, evaluate the prediction using various evaluation metrics.
Note that lazy learning algorithms like the constant models or memory-based algorithms may skip the second step.
A simple train and test split is constructed by choosing a certain proportion of all ratings as test set and assigning the remaining ratings to the train set. In addition to this, K-fold cross-validation is also supported.
2.3 Data Structures
PREA uses a sparse matrix representation for the rating matrices which are generally extremely sparse (users provide ratings for only a small subset of items). Specifically, we use Java’s data structure HashMap to create a DataMap class and a SparseVector class. We tried some other options including TreeMap, but we chose HashMap due to its superior performance over others. Figure 2 (left) shows an example of a sparse vector, containing data only in indices 1, 3, and 6.
We construct a SparseMatrix class using an array of SparseVector objects. To facilitate fast access to rows and columns, both row-oriented and column-oriented arrays are kept. This design is also useful for fast transposing of sparse matrices by interchanging rows and columns. Figure 2 (right) shows an example of sparse matrix.
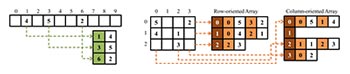
Figure 2: Sparse Vector (left) and Matrix (right) Implementation
PREA also uses dense matrices in some cases. For example, dense representations are used for low-rank matrix factorizations or other algebraic operations that do not maintain sparsity. The dense representations are based on the matrix implementations in the Universal Java Matrix Package (UJMP) (http://www.ujmp.org/).
2.4 Implemented Algorithms and Evaluation Metrics
PREA implements the following prediction algorithms:
• Baselines (constant, random, overall average, user average, item average): make little use of personalized information for recommending items.
• Memory-based Neighborhood algorithms (user-based, item-based collaborative filtering and their extensions including default vote, inverse user frequency): predict ratings of unseen items by referring those of similar users or items.
• Matrix Factorization methods (SVD, NMF, PMF, Bayesian PMF, Non-linear PMF): build low-rank user/item profiles by factorizing training data set with linear algebraic techniques.
• Others: recent state-of-the-art algorithms such as Fast NPCA and Rank-based collaborative filtering.
We provide popular evaluation metrics as follows:
• Accuracy for rating predictions (RMSE, MAE, NMAE): measure how much the predictions are similar to the actual ratings.
• Rank-based evaluation metrics (HLU, NDCG, Kendall’s Tau, and Spearman): score depend- ing on similarity between orderings of predicted ratings and those of ground truth.
3. Related Work
Several other open-source recommendation toolkits are available. Table 1 summarizes the imple- mented features in these toolkits and compares them to those in PREA. Mahout,3 which incor- porated Taste,4 provides an implementation of many memory-based algorithms. It also supports powerful mathematical and statistical operations as it is a general-purpose machine learning toolkit. Duine5 provides a way to combine multiple algorithms into a hybrid system and also addressed the cold-start situation. Cofi6 implements several traditional algorithms with a simple design based on providing wrappers for publicly available data sets. MyMedia7 is a C#-based recommendation toolkit which supports most traditional algorithms and several evaluation metrics.
As indicated in Table 1, existing toolkits widely provide simple memory-based algorithms, while recent state-of-the-art algorithms are often not supported. Also, these toolkits are generally limited in their evaluation metrics (with the notable exception of MyMedia). In contrast, PREA pro- vides a wide coverage of the the most up-to-date algorithms as well as various evaluation metrics, facilitating a comprehensive comparison between state-of-the-art and newly proposed algorithms in the research community.
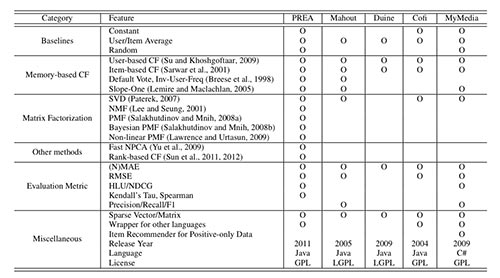
Table 1: Comparison of Features with other Collaborative Filtering Toolkits
4. Summary
PREA contributes to recommendation system research community and industry by (a) providing an easy and fair comparison among most traditional recommendation algorithms, (b) supporting state-of-the-art recommendation algorithms which have not been available on other toolkits, and (c) implementing different evaluation criteria emphasizing different performance aspects rather than a single evaluation measure like mean squared error.
The open-source nature of the software (available under GPL) may encourage other recommen- dation systems experts to add their own algorithms to PREA. More documentation for developers as well as user tutorials are available on the web (http://prea.gatech.edu).
References
- J. Breese, D. Heckerman, and C. Kadie. Empirical analysis of predictive algorithms for collaborative filtering. In Proc. of Uncertainty in Artificial Intelligence, 1998.
- A. Gunawardana and G. Shani. A survey of accuracy evaluation metrics of recommendation tasks. Journal of Machine Learning Research, 10:2935–2962, 2009.
- N. D. Lawrence and R. Urtasun. Non-linear matrix factorization with gaussian processes. In Proc. of the International Conference of Machine Learning, 2009.
- D. Lee and H. Seung. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems, 2001.
- J. Lee, M. Sun, S. Kim, and G. Lebanon. Automatic feature induction for stagewise collaborative filtering. In Advances in Neural Information Processing Systems, 2012a.
- J. Lee, M. Sun, and G. Lebanon. A comparative study of collaborative filtering algorithms. ArXiv Report 1205.3193, 2012b.
- D. Lemire and A. Maclachlan. Slope one predictors for online rating-based collaborative filtering. Society for Industrial Mathematics, 5:471–480, 2005.
- A. Paterek. Improving regularized singular value decomposition for collaborative filtering. Statis- tics, 2007:2–5, 2007.
- R. Salakhutdinov and A. Mnih. Probabilistic matrix factorization. In Advances in Neural Informa- tion Processing Systems, 2008a.
- R. Salakhutdinov and A. Mnih. Bayesian probabilistic matrix factorization using markov chain monte carlo. In Proc. of the International Conference on Machine Learning, 2008b.
- B. Sarwar, G. Karypis, J. Konstan, and J. Reidl. Item-based collaborative filtering recommendation algorithms. In Proc. of the International Conference on World Wide Web, 2001.
- X. Su and T. M. Khoshgoftaar. A survey of collaborative filtering techniques. Advances in Artificial Intelligence, 2009:4:2–4:2, January 2009.
- M. Sun, G. Lebanon, and P. Kidwell. Estimating probabilities in recommendation systems. In Proc. of the International Conference on Artificial Intelligence and Statistics, 2011.
- M. Sun, G. Lebanon, and P. Kidwell. Estimating probabilities in recommendation systems. Journal of the Royal Statistical Society, Series C, 61(3):471–492, 2012.
- K. Yu, S. Zhu, J. Lafferty, and Y. Gong. Fast nonparametric matrix factorization for large-scale collaborative filtering. In Proc. of ACM SIGIR Conference, 2009.