Abstract
INTRODUCTION
In clinical practice cranio-maxillo-facials surgeon permanently needs to have accurate and objective information about the structure, shape and size of the patient`s hard and soft tissues. It is necessary to assess the specific situation, the planning and preparation for future operations. For the acquisition and processing of diagnostic information X-ray, angiography, ultrasound, CT and / or MRI, and photogrammetric measurement (stereoscopic shooting) are currently used. Each of these methods requires specialized knowledge to interpret the information received. However, even an experienced surgeon is forced to use his imagination in order to build the whole picture of the pathology and make the right decision based on the computer image or X-rays. Therefore an important issue is the conversion of diagnostic information to the more convenient form of perception in human terms.
New technology of rapid prototyping was being actively implemented in recent years. One of the most popular technology is laser stereolithography. This technology represents a layered manufacturing of plastic copy of the object based on its computer image. Application of this technology in medicine is based on obtaining a three-dimensional digital model of the object, using the data of computer tomography or magnetic resonance imaging. [1]
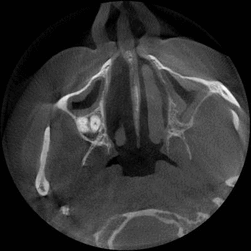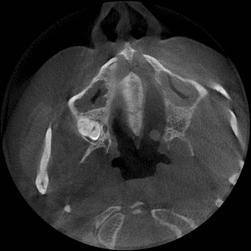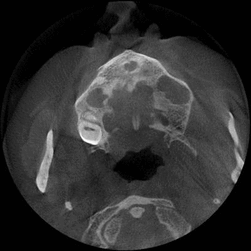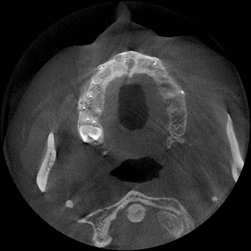
Figure 1 – SCT images (animation: 7 frames, 12 repeat cycles, time between frames - 1sec., size: 183 kb)
RELEVANCE OF THE TOPIC
Treatment of injuries maxillofacial region is one of the urgent tasks of maxillofacial surgery. According to statistics, the victims of injuries maxillofacial constitute about 25% of all maxillofacial`s patients. There has been an increase in the number of severe injuries facial bones. The percentage of complications is high (15-25%). [2] The ability to produce plastic models of operated areas would be extremely useful.
GOAL AND OBJECTIVES OF THE STUDY
The goal of this work is to design a decision support system (DSS) for the construction of three-dimensional model of the maxillofacial region based on the SCT data and determine mounting points of the implant-fixing in fractures.
DSS directed to elimination the deficiencies of existing similar systems, medical assistance in preparation for implantation by providing information of possible points of attachment of the implant.
To achieve this goal it is necessary to solve the following problems:
- subject of study analysis, formulation of the problem;
- review and analysis of existing systems related to the processing of images of the maxillofacial region;
- review, analysis and selection of image processing techniques;
- analysis and development of approaches to determining optimal implant attachment points;
- analysis, selection and development of methods of constructing three-dimensional model;
- development of DSS structure, the definition of its subsystems and functional units;
- choice of systems instrument and technology development;
- establishment of DSS and its testing in real conditions;
- analysis of the DSS testings results.
The object of research is the process of implantation in oral and maxillofacial surgery.
The subject of the study is determination of parameters and implant attachment points in maxillofacial surgery.
3D MODEL CONSTRUCTION
One of the key problems in the master's work is to build a three-dimensional model based on the SKT data. We use "marching cubes" algorithm to solve this problem. [4]
This algorithm produces a partition of the space containing the original surface into cubic cells. Then this algorithm approximates the intersection of the surface and each cubic cell splitting by triangles(figure 2).
The process of constructing three-dimensional model can be divided into two stages:
- Split the area G of the space R3 into a finite set of cells, cell search, crossed the desired surface.
- Approximation of surface cells found. [4]
Figure 2 – marching cubes
The algorithm determines how the surface intersects this cube, then moves (or marchs) to the next cube. To find the surface intersection in a cube, we assign a one to a cube's vertex if the data value at that vertex exceeds (or equals) the value of the surface we are constructing. These vertices are inside (or on) the surface. Cube vertices with values below the surface receive a zero and are outside the surface. The surface intersects those cube edges where one vertex is outside the surface (one) and the other is inside the surface (zero).
Since there are eight vertices in each cube, and two possible values, inside and out, there are only 28= 256 ways with which the surface can interfere with the cube. However, the rotation symmetry and using these methods can be reduced to 15 represented on figure 3.
Figure 3 – triangulated cubes
The simplest pattern, zero, occurs if all vertex values are above (or below) the selected value and produces no triangles. The next pattern, first, occurs if the surface separates on vertex from the other seven, resulting in one triangle defined by the three edge intersections. Other patterns produce multiple triangles. Permutation of these 14 basic patterns using complementary and rotational symmetry produces the 256 cases.
We create an index for each case, based on the state of the vertex. Using the vertex numbering on figure 4, the eight bit index contains one bit for each vertex.
Figure 4 – Cube Numbering
This index serves as a pointer into an edge table that gives all edge intersections for a given cube configuration. Using the index to tell which edge the surface intersects, we can interpolate the surface intersection along the edge.
The final step in marching cubes calculates a unit normal for each triangle vertex. The rendering algorithms use this normal to produce Gouraud-shaded images. A surface of constant density has a zero gradient component along the surface tangential direction; consequently, the direction of the gradient vector, g , is normal to the surface. We can use this fact to determine surface normal vector, n, if the magnitude of the gradient, |g| , is nonzero. Fortunately, at the surface of interest between two tissue types of different densities, the gradient vector is nonzero. The gradient vector, g, is the derivative of the density function.
To estimate the gradient vector at the surface of interest, we first estimate the gradient vectors at the cube vertices and linearly interpolate the gradient at the point of intersection. The gradient at cube vertex (i,j,k) is estimated using central differences along the three coordinate axes by:
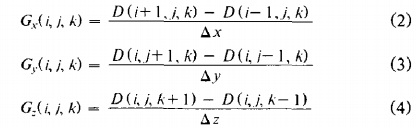 ,
,
where (i,j,k) is the density at pixel (i, j) in slice k and Ax, Ay, Az are the lengths of the cube edges. Dividing the gradient by its length produces the unit normal at the vertex required for rendering. We linearly interpolate this normal to the point of intersection.
In summary, marching cubes creates a surface from a three-dimensional set of data as follows:
- Read four slices into memory.
- Scan two slices and create a cube from four neighbors on one slice and four neighbors on the next slice.
- Calculate an index for the cube by comparing the eight density values at the cube vertices with the surface constant.
- Using the index, look up the list of edges from a precalculated table.
- Using the densities at each edge vertex, find the surfaceedge intersection via linear interpolation.
- Calculate a unit normal at each cube vertex using central differences. Interpolate the normal to each triangle vertex.
- Output the triangle vertices and vertex normals. [3]
CONCLUSION
In this paper we collected and studied materials on issues related to the theme of master's work.
We allocated tasks which will be solved in the master's work. We considered a similar works. We identified strengths and weaknesses of existing tools to construct three-dimensional models of the maxillofacial region. "Marching cubes" algorithm for constructing a three-dimensional model based on the SCT data was considered.
We chose the direction of own researches of constructing three-dimensional models of the implant and the search for optimal parameters of attachment in mandibular fractures based on the analysis results.
NOTE
In writing this essay master's work is not yet complete. Final completion: May 2017. The full text of work and materials of the topic can be obtained from the author or his scientific adviser after that date.
SOURCES
- A. Ivanov. The use of computer and stereolithography biomodeling in Children's Maxillofacial Surgery, Moscow, 2003, 14.00.21, 151p.
- D. Kalinowski, I.N.Matros-Taranets. Current approaches to diagnosis, treatment and rehabilitation of injuries maxillofacial area with the use of computer technology and telemedicine. Volume 7, ¹1, 2009.
- William E. Lorensen, Harvey E. Cline: Marching Cubes: A high resolution 3D surface construction algorithm. In: Computer Graphics, Vol. 21, Nr. 4, July 1987
- Bugrov N. Golubev V., Klimenko A., Dizhevsky A., Oboimov A., Kakauridze D., Frolov P. Overview of triangulation algorithms, implicit surface, MEDIAS2012 Proceedings of the International Scientific Conference, 07-14 May 2012, Limassol, Cyprus, Izd.IFTI, S.151-173, ISBN 978-5-88835-023-2
- Planmeca Oy – Dental software – Planmeca Romexis [electronic resource] – Access mode to article: http://www.planmeca.com/en/dental_software/planmeca_romexis
- SPP KORONIDA: concept, principles of operation, the use of telemedicine / D Kalinowski, I. Matros-Taranets, A. Ponomarenko, O. Chengar // Ukr.zh.telemed.med.telemat. -2008. - T.6, ¹1. - S.19-24. 14.
- Osirix Imaging Software – About Osirix[electronic resource] – Access mode to article: http://www.osirix-viewer.com/AboutOsiriX.html
- Materialise Mimics[electronic resource] – Access mode to article: http://biomedical.materialise.com/mimics
- Galanin M., Scheglov I. Development and implementation of algorithms for three-dimensional triangulation complex spatial areas: iterative methods, Moscow 2006
- Baradeswaran.A, Joshua Selvakumar.L, Padma Priya.R, Reconstruction of Images into 3D Models using CAD Techniques, European Journal of Applied Engineering and Scientific Research, 2014, 3 (1):1-8
