Исследование методов динамического отображения графической информации при использовании полярной системы координат
Автор:
Шулянский Д.В.
Источник: Международная научно-техническая конференция студентов и молодых учёных. — Донецк, ДонНТУ - 1015.
Шулянский Д.В. Исследование методов динамического отображения графической информации при использовании полярной системы координат. Выполнен анализ светодиодных дисплеев. Выбран один из возможных методов динамического отображения изображения, а также выполнен анализ необходимых мер по достижению поставленной цели.
Поскольку динамический метод отображения изображения должен быть реализован на микроконтроллере, необходим эффективный метод адресации пикселей при использовании полярной системы координат.
Светодиодные дисплеи представляют собой прямоугольную матрицу, элементами которой являются светодиоды. Каждый светодиод обладает координатой Х и Y, с помощью которых происходит адресация пикселей, основываясь на декартовой системе координат.
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
Прямоугольная система координат — прямолинейная система координат (рисунок 1) с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности.
Рисунок 1. Прямоугольная система координат.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом (рисунок 2). Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом.
Каждая точка в полярной системе координат может быть определена двумя полярными координатами, что обычно называются
(радиальная координата, угловое расстояние, встречается вариант
) и
(угловая координата, полярный угол, азимут,
позиционный угол
, иногда пишут
или
). Координата
соответствует расстоянию до полюса, а координата
равна углу в направлении против часовой стрелки от луча через 0° (иногда называется полярной осью).
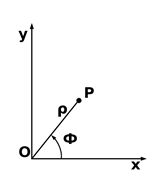
Рисунок 2. Полярная система координат.
Исследовав полярную систему координат, обнаруживаем, что данная система более удобна при представлении радиальных кривых. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра.
Делаем вывод, что необходимый метод предоставления информации должен иметь форму круга, но в таком случае возникают сложности при корректном отображении данных при отдалении от центра экрана. Решением данной проблемы может являться следующий метод отображения изображения:
На отрезке ОР (рисунок 2) устанавливаем некоторое количество светодиодов. Пусть точка О будет осью вращения отрезка ОР. В таком случае начиная с определённой частоты вращения отрезка (порядка 50 раз в секунду) вокруг выбранной оси будет создаваться впечатление, будто перед нами не светодиодная линейка, а полноценный экран. В таком случае координаты каждого светодиода могут быть переведены в декартову систему координат при помощи следующих тригонометрических функций:
X = r cos(µ),
Y = r sin(µ).
Используя данные координаты, можем с лёгкостью указать цвет свечения светодиода на отрезке ОР в определённый момент времени.
1. Полярная система координат (полярные координаты)/ Интернет-ресурс. - Режим доступа: www/ URL: http://mathhelpplanet.com/static.php?p=polyarnye-koordinaty - Загл. с экрана.
2. Декартова система координат/ Интернет-ресурс. - Режим доступа: www/ URL: http://www.mathematics.ru/courses/function/content/chapter1/section2/paragraph1/theory.html#.VXccrs_tmko - Загл. с экрана.
3. Современные светодиодные экраны_ Характеристики, технологии, критерии выбора/ Интернет-ресурс. - Режим доступа: www/ URL: http://www.screens.ru/ru/2011/12.html - Загл. с экрана.