Обзор методов нечеткого поиска текстовой информации
Автор: П.М. Мосалев
Источник: Журнал "Вестник Московского государственного университета печати" Выпуск № 2 / 2013.
Нечеткий поиск - это поиск информации, при котором выполняется сопоставление информации заданному образцу поиска или близкому к этому образцу значению. Алгоритмы нечеткого поиска используются в большинстве современных поисковых систем, например, для проверки орфографии [1].
Рассмотрим задачу нечеткий поиск текстовой информации. В данном случае задача может принимать следующий вид: есть текстовая информация определенного размера, пусть пользователь вводит слово или фразу для поиска, необходимо найти в тексте все совпадения с заданным словом с учетом возможных допустимых различий. Например, при запросе пользователя «интернет» нужно найти «интерн», «интернат» и другие слова.
Как же можно оценить сходство двух слов в тексте? Для этого используются специальные метрики нечеткого поиска. Метрикой нечеткого поиска называют функцию расстояния между двумя словами, позволяющую оценить степень их сходства в данном контексте. В качестве метрик используют расстояния Хемминга, Левенштейна, Дамерау- Левенштейна.
Расстояние Хемминга - это число позиций, в которых соответствующие символы двух слов одинаковой длины различны [2]. Согласно определению, расстояние Хемминга имеет один существенный недостаток - сравнивать можно только слова одинаковой длины. Из-за этого данную метрику практически не применяют на практике.
Расстояние Левенштейна или расстояние редактирования - это минимальное количество операций (вставки одного символа и замены одного символа на другой), необходимых для преобразования одной строки в другую [1]. Расстояние Левенштейна применяют для исправления ошибок в словах, биоинформатике для сравнения хромосом и для полнотекстового поиска. Данная метрика имеет следующие недостатки:
Расстояние Левенштейна может быть велико для больших похожих слов, но при этом, если есть два коротких слова значительно отличающихся друг от друга, то тогда расстояние Левенштейна будет мало.
Расстояние Дамерау-Левенштейна - это мера разницы двух строк символов, определяемая как минимальное количество операций вставки, удаления, замены и перестановки соседних символов, необходимых для перевода одной строки в другую. Данная метрика отличается от расстояния Левенштейна только добавлением новой операции (перестановки).
Для расчета расстояния Левенштейна используют метод Вагнера-Фишера. Составляем матрицу преобразований по формуле указанной на рис. 1.
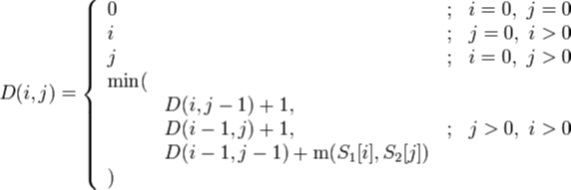
Рис. 1. Вычисление матрицы преобразования
При расчете матрицы используются обозначения: S1, и S2 - сравниваемые слова, S1[i] - i-й символ слова, m(S1[i], S2[j]) - 1, если S1[i] = S2[j] или 0 в противном случае. В результате будет составлена матрица преобразования символов, где ее значения - это расстояния для преобразования символов. Итоговым значением преобразования одной строки в другую будет элемент с максимальными индексами. Пример такой матрицы преобразования представлен на рис. 2.
Итоговое расстояние между словами «дагестан» и «арестант» будет равно 3.
Данный алгоритм требует довольно значительных затрат памяти и времени выполнения. Однако он может быть упрощен путем сокращения количества вычислений. Сравнение строк может происходить с учетом морфем, так могут подвергаться трансформации только суффиксы слов или окончания. Другим вариантом снижения затрат может быть использование ограничений по количеству сравнений.
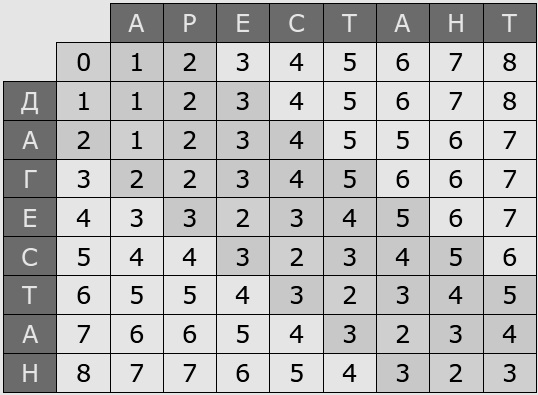
Рис. 2. Матрица преобразования для двух слов
Согласно [3] при реализации данного метода для мобильного приложения для проверки корректности ввода слова, приложение работало больше минуты. При этом был использован словарь объемом 90 000 слов.
Другим вариантом реализации нечеткого поиска может служить алгоритм хеширования по сигнатуре. Данный метод основан на составлении специальных хеш-таблиц слов. При этом каждому слову в тексте в соответствие ставится битовая маска (сигнатура).
Сигнатурой sign(w) слова w будем называть вектор размерности m, k-й элемент которого равняется единице, если в слове w есть символ a такой, что f(a)=k, и нулю в противном случае. Номером сигнатуры слова будем называть число H(w) =SUM((2^i)*sign(w)[i+1]) [4].
Данный метод требует значительных временных затрат на составление хеш-таблиц. Что так же затрудняет его использование в мобильных приложениях. Однако данный метод достаточно прост при реализации и позволяет выполнять быстрый поиск как по полному совпадению слова, так и при наличии одной или двух ошибок в слове. Проблема временных затрат может быть решена путем создания готовых индексов по текстам или словарям. Так же можно перенести индексы на мобильное устройство и записать их в базу данных реализованную средствами SQLite.
Алгоритм расширения выборки основан на составлении наиболее возможных вариантов изменения слова. При этом может быть задано количество возможных ошибок. Данный метод достаточно удобен при работе со словарем. Фактически данный метод является своеобразной реализацией метода Вагнера-Фишера, но с учетом того, что будут искаться не все возможные изменения, а только часто встречаемые. Данный метод ускоряет поиск, но может не дать желаемый результат и значительно замедляется при увеличении словаря.
При сравнении двух строк или слов, с учетом максимально возможного количества расхождений можно выделить в словах (строках) общие части. После чего можно выполнять поиск по таким частям. Такой метод получил название метод N-грамм, а совпадения и являются N-граммами. Метод N-грамм состоит из нескольких этапов:
1. Составляются индексные базы по указанным N-граммам.
2. После чего введенное слово для поиска тоже разбивается на N-граммы.
3. После чего выполняется полный перебор значений по указанным N-граммам.
Пример такого метода показан на рис. 3.
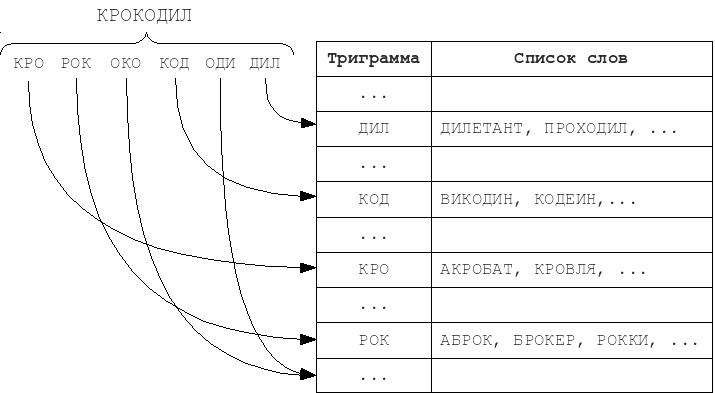
Рис. 3. Поиск ошибок методом N-грамм
Метод N-грамм не всегда находит ошибки. Данная проблема происходит, например, когда пользователь ошибся в одной букве в корне слова при вводе. Так же данный метод при обращении к базе данных каждый раз будет выполнять перебор 10-20% информации. При наличии словарей больших размеров данный метод будет долго выполняться и требовать больших ресурсов и мощностей, что достаточно затруднительно при работе с мобильными устройствами.
При оптимизации нечеткого поиска часто возникает вопрос по организации данных таким образом, чтобы поиск выполнялся быстрее и тратил меньше ресурсов. Одним из вариантов подобной организации данных служат деревья В. Буркхарда и Р. Келлера (BK-деревья). Данные деревья строятся на основании метрик Левенштейна или Даме- рау-Левенштейна. Пример такого дерева представлен на рис. 4.
Данный метод позволяет сократить время выполнения поиска за счет более удобной структуры данных, однако усложняет алгоритм поиска.
В заключение хотелось бы сказать, что были рассмотрены наиболее известные методы нечеткого поиска текстовой информации:
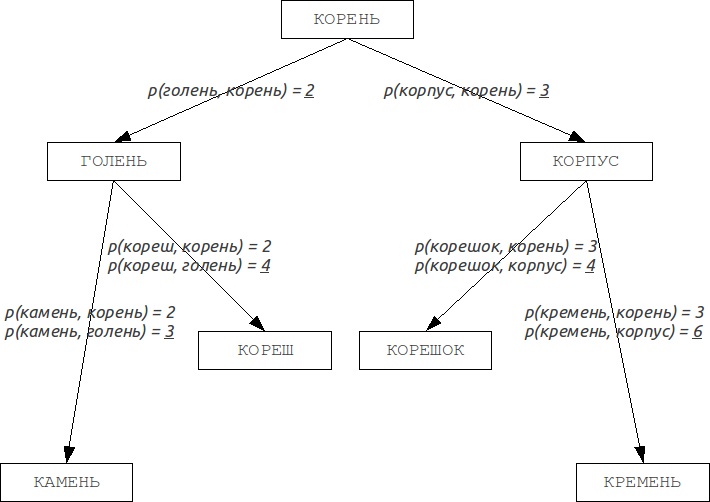
Рис. 4. Дерево Буркхарда и Келлера
Метод Вагнера-Фишера, метод N-грамм, метод хеширования по сигнатуре, алгоритм расширения выборки, деревья Буркхарда-Келлера. Каждый из данных методов имеет свои достоинства и свои недостатки.
Ключевым недостатком данных методов является время выполнения поиска. При работе с мобильными устройствами время является важным критерием работы приложения. Однако данные методы можно оптимизировать за счет их комбинаций или внесения дополнительных условий, задаваемых пользователем или разработчиком.
1. Нечеткий поиск в тексте и словаре - http://habrahabr.ru/ post/114997/
2. Конышева Л.К. Основы теории нечетких множеств : учеб. пособие / Л.К. Конышева, Д.М. Назаров. - СПб. : Изд-во. Питер, 2011 - 192 с.
3. Нечеткий поиск слова на платформе iOS - http:// habrahabr.ru/post/136406/
4. БойцовЛ.М. Использование хеширования по сигнатуре для поиска по сходству. Прикладная математика и информатика / Л.М. Бойцов. - М. : Изд-во факультета ВМиК, МГУ, 2000. - № 7. КОРЕНЬ