Реферат з теми випускної работи
Зміст
- Введення
- 1. Модальне регулювання
- 2. Фільтр Калмана
- 3. Опис об'екта керування
- 4. Синтез системи керування
- Висновки
- Список джерел
Введення
У сучасних системах все частіше використовуються багатомасові моделі. Ця робота буде проводитися на моделі механізму переміщення моста мостового крану з метою гасіння, виникаючих за рахунок довжини мосту пружних коливань, які призводять до значних неприємностей при роботі з таким механізмом. Це можуть бути такі неприємні явища, як розгойдування, переміщуваного краном, вантажу, що може погіршити виробничий процес і привести до падіння продуктивності пристрою. Також не менш важливим аспектом є те, що при такій роботі виникаючі пружні коливання поступово призводять до втоми матеріалу і як наслідок раннього виходу з ладу всього механізму і таким чином спричинить за собою зупинку всього виробничого процесу на час ремонту крана. У даній роботі буде проведено синтез системи керування, яка могла б усунути пружні коливання. Для керування такою системою будемо використовувати модальний регулятор. Особливістю роботи модального регулятора є те, що для функціонування йому необхідний весь вектор стану керованої системи, але з огляду на те, що безпосередньо з об'єкта керування, найчастіше, ми не можемо отримати всі змінні стану системи, необхідні для роботи модального регулятора з огляду на те, що досить часто ці величини не можуть бути безпосередньо отримані за допомогою датчиків, так які можуть бути складно або взагалі невимірними. В основному з об'єкта ми можемо отримати мінімум таких змінних. Наприклад, швидкість будь-яких ланок і струм у колі, напруга, що подається на двигун і кут повороту валу двигуна. Для отримання решти змінних стану необхідно використовувати спостерігач стану системи, який буде синтезований на основі математичної моделі об'єкта і зможе дати весь необхідний для роботи модального регулятора вектор стану системи. Однак сигнал, одержуваний з реальних датчиків, дуже часто надходить в систему керування сильно зашумлений і тим самим може порушити роботу всієї системи. Для того щоб уникнути подібних збоїв роботи системи через шум, отриманий з датчиків, необхідно використовувати фільтр який позбавив би сигнал від шумів. В якості такого фільтра може служити фільтр Калмана, який є дуже потужним інструментом, він може не тільки фільтрувати сигнал отриманий з датчиків, грунтуючись на математичну модель він може надати весь вектор стану системи. Таким чином використовуючи ці два потужних інструменти разом, ми можемо реалізувати систему керування без застосування стороннього спостерігача і отримати при цьому максимально можливо достовірні відфільтровані показники датчиків. Так само в даній роботі проведені випробування отриманої моделі при різних рівнях дискретності системи керування і зроблені висновки з приводу працездатності фільтра Калмана при даних змінах.
1. Модальне регулювання
Суть модального регулювання полягає в кореневому методі синтезу лінійної САР, тобто виходячи з необхідних і бажаних показників якості управління потрібно побудувати бажаний характеристичний поліном. Це означає що потрібно визначити місце розташування коренів характеристичного полінома. (У перекладі з латинської мови - це коріння, звідси і виходить назва регулятора - модальний регулятор).
Суть модального регулювання полягає в кореневому методі синтезу лінійної САР, тобто виходячи з необхідних і бажаних показників якості керування потрібно побудувати бажаний характеристичний поліном. Це означає що потрібно визначити місце розташування коренів характеристичного полінома. (У перекладі з латинської моди - це корені, звідси і виходить назва регулятора - модальний). Принцип модального регулятора полягає в розрахунку коефіцієнтів зворотного зв'язку по змінним стану, що забезпечують задані показники якості. [1]
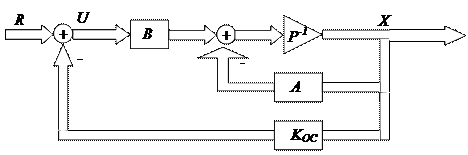
Рисунок 1 – Принцип модального регулювання
В систему потрібно ввести новий вектор вхідних сигналів U - вектор керуючих впливів, зв'язок якого зі старим вхідним вектором R забезпечується рівнянням U=R-KocX. В такому випадку наша система диференціальних рівнянь, яка описує динаміку нашої системи прийме наступний вигляд:
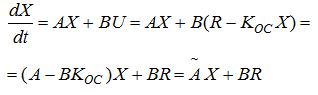
Для того щоб синтезувати працездатний регулятор, необхідно упевнитися, що отриманий нами об'єкт є повністю керованим і спостерігаємим.
Поняття повної керованості має на увазі, що ми можемо перевести об'єкт з початкового стану у будь-яке задане нами положення при поданні обмеженого керуючого впливу. Спостереження, в свою чергу, це можливість по вихідній вектору визначити вектор стану системи.
Для того щоб переконатися в тому, що система спостерігаєма і керована ми можемо використовувати критерій Калмана, який має на увазі перевірку рангів матриць керованості U спостереження та V:
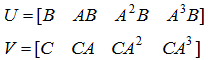
Для того щоб вважати систему повністю керованою і спостерігаємою нам необхідно, щоб ранги матриць U і V відповідали порядку нашої системи.
Як нам відомо, динаміку перехідних процесів визначають корені характеристичного полінома. Таким чином, визначаючи бажаний характер перехідного процесу заданого полінома, можливо досягти необхідних для нас показників якості.
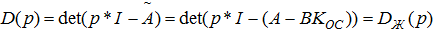
Де Dж(p) - бажаний характеристичний поліном, визначений виходячи із заданих показників якості регулювання за методикою непрямої кореневої оцінки.
Таким чином, вирішуючи цю систему рівнянь щодо невідомих нам коефіцієнтів Koc можна визначити необхідні для нас коефіцієнти негативного зворотного зв'язку по вектору стану Х, які і будуть представляти із себе модальний регулятор. Але не можна розраховувати на те, що ми можемо таким чином реалізувати будь-який перехідний процес для будь-якої системи просто підставивши в якості бажаних будь-які коріння, так як в процесі створення регулятора передбачається, що система лінійна, що насправді не так, і таким чином ми можемо синтезувати регулятор тільки для цієї лінійної частини системи.
2. Фільтр Калмана
Фільтр Калмана - ефективний рекурсивний фільтр, який оцінює вектор стану динамічної системи, використовуючи ряди неповних і зашумлених вимірювань. Названий на честь Рудольфа Калмана. Фільтр Калмана широко використовується в різних інженерних та економетричних додатках: від радарів і систем машинного зору до оцінок параметрів макроекономічних моделей. Калманівська фільтрація є важливою частиною теорії керування, вона відіграє величезну роль у створенні систем керування.
Фільтр Калмана призначений для рекурсивного дооцінювання вектора стану спочатку відомої динамічної системи, таким чином для того, щоб розрахувати поточний стан системи потрібно мати поточний вимір, а також попередній стан самого фільтра. Роботу алгоритму можна розділити на два етапи: етап прогнозування та етап уточнення отриманого значення на основі отриманого сигналу вимірювання. На першому етапі (етапі прогнозування) фільтр Калмана екстраполює значення змінних стану, а також їх невизначеності, таким чином отримуючи приблизне значення яке може прийняти шуканий нами сигнал. На другому етапі (етапі уточнення), за даними отриманих за допомогою вимірювання реального сигналу (отриманого з деякою погрішністю), результат першого етапу уточнюється. Завдяки такій покрокової реалізації алгоритму, фільтр може відстежувати в реальному часі стан спостережуваного нами об'єкта. [2]
3. Опис об'єкта керування
Об'єктом управління став механізм переміщення моста мостового крана.
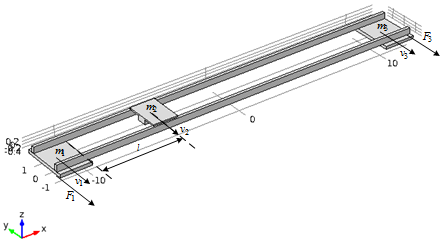
Рисунок 2 – Об'ект керування
Для того щоб максимально спростити нашу модель, міст представимо у вигляді двох суцільнометалевих профілів з прямокутним перетином і заниженими значеннями щільності і модуля пружності матеріалу так, щоб маса конструкції приблизно відповідала реальним даним. Візок в даному випадку буде зафіксований в одному положенні і буде моделюватися як складова частина конструкції моста. Далі розташуємо візок посередині моста і докладемо до крайніх частин нашої конструкції зусилля, яке відповідає розгону моста до швидкості 0.3 м / с за 1 с при відпрацюванні трапецеїдального закону зміни швидкості. [3]
Графіки зміни швидкостей крайніх точок моста v1 і візку v2, який має місце в його середній точці, наведені на рис. 3. На даних графіках чітко видно, що розглянуті точки конструкції роблять незгасаючі коливання, які поступово зменшують її міцність і надалі можуть стати причиною виходу крану з роботи і травм персоналу.
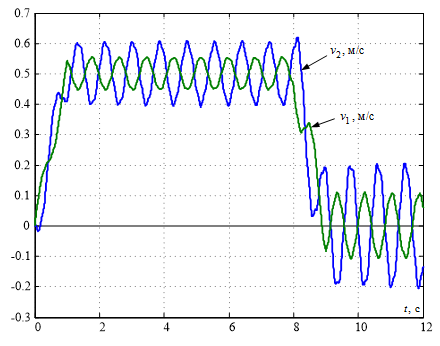
Рисунок 3 – Графік перехідних процесів швидкостей руху пружної конструкції мостового крану
Для того, щоб гасити ці незгасаючі коливання необхідно синтезувати відповідну систему керування швидкістю моста, що вимагає наявності лінійної математичної моделі об'єкта регулювання.
У нашому випадку математичну модель об'єкта можна скласти на підставі кінематичних схем багатомасових систем, наведених на рис.4.
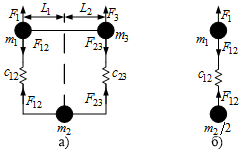
Рисунок 4 – Кінематичні моделі моста
На рис.4а міст умовно представлений у вигляді трьох зосереджених мас - крайніх точок m1 і m3, пов'язаними пружними зв'язками з коефіцієнтами жорсткості с12 і с23 з точкою m2, в якій знаходиться візок.
Якщо ми розташуємо візок прямо посередині моста (L1 = L2), то і коефіцієнти жорсткості пружних зв'язей також повинні бути однаковими. Якщо при такому розташуванні елементів рівні між собою і маси, які зосереджені на кінцях моста, а також додані до них сили, на однаковій відстані від опор, маси яких дорівнюють, то кінематичну схему нашого об'єкта керування можна спростити до двумасової, залишивши одну опору і центральну точку, масу якої слід зменшити в 2 рази. Кінематична схема для такого випадку представлена на рис.4б. Її математичний опис буде мати такий вигляд:
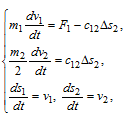
де F1 - сила, яку додають до першої маси, F2 - пружна сила, Δs2=s1-s2 - величина пружної деформації.
Якщо ми знаємо значення зосереджених мас і постійної часу пружних коливань двумасової системи T12=1/2/pi/f, то ми зможемо розрахувати коефіцієнт жорсткості: [3]
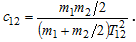
Де:
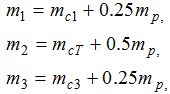
Таким чином, ввівши деякі припущення і спрощення ми перетворили складну тримасову кінематичну систему в більш просту двомасову модель, на якій буде набагато легше проводити досліди і реалізовувати систему керування з метою гасіння шкідливих для об'єкта пружних коливань.
4. Синтез системи керування
Одним із способів гасіння даних коливань є використання модального регулятора. Для того, щоб синтезувати даний регулятор необхідно перевести нашу систему в простір стану, для цього необхідно перетворити дані рівняння в матриці простору стану:
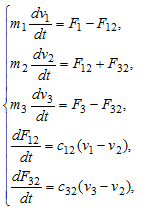
Вектор вхідних сигналів дорівнює:
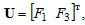
Вектор змінних стану
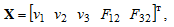
Матриця стану А дорівнює:
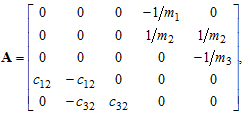
Вхідна матриця В дорівнює:
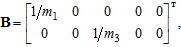
У пакеті Simulink була синтезована модель, що включає об'єкт керування в просторі станів, модальний регулятор і фільтр Калмана (рис. 5)
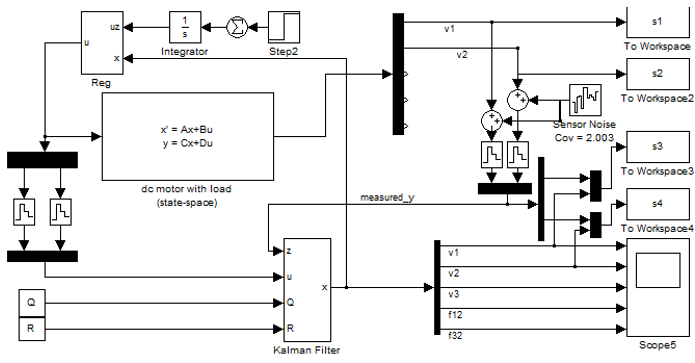
Рисунок 5 – Модель для випробувань
На даній моделі розташовані такі елементи як модель об'єкта в просторі стану, яка заснована на матрицях стану нашого об'єкта керування (state-space), модальний регулятор (Reg) реалізований як негативний зворотний зв'язок по вектору стану об'єкта, який отриманий з виходу фільтра Калмана (Kalman Filter), на вхід якого подаються зашумлені сигнали швидкості з об'єкта керування, а також керуючий вплив як і на об'єкт керування, але з дискретизацією сигналу по рівню, щоб імітувати дискретну систему керування. Так само блоки дискретизації і виведення даних в робочий простір Matlab для отримання графіків перехідних процесів. Також можна побачити блок Step і Integrator, які виконують функцію завдання трапецеїдального закону керування.
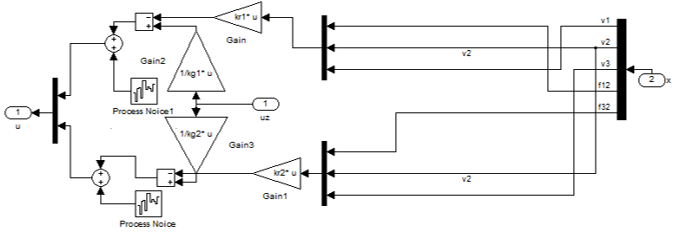
Рисунок 6 – Вміст блоку Reg
У блоці Reg розташовані такі об'єкти як коефіцієнти зворотного зв'язку, які є модальним регулятором і блоки Process Noise, які вносять в систему керування похибку, відражаючу неточність опису моделі об'єкта, яку в загальному випадку не можна обчислити, але можна підібрати, домігшись максимально якісних результатів.
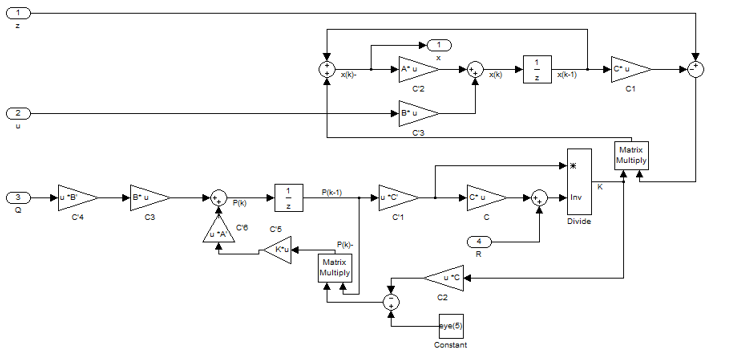
Рисунок 7 – Вміст блока Kalman Filter
На рис.7 представлено вміст фільтра Калмана, де на вхід подаються такі сигнали, як керуючий вплив, зашумлені сигнали, які були зняті з об'єкту керування і зашумлені, з метою імітації роботи реального датчика, також на вхід фільтра подаються величини, що характеризують коваріацію шуму датчика і системи. Коваріація датчика може бути отримана дослідницьким шляхом за вибіркою сигналу з реального датчика. Коваріація моделі не може бути отримана таким чином і підбирається вручну.
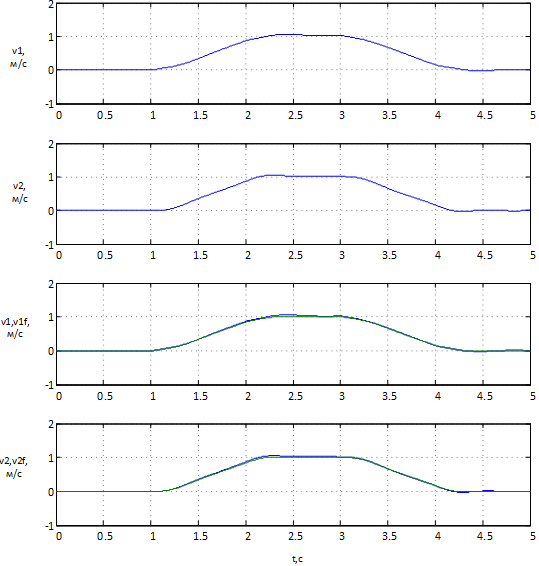
Рисунок 8 – Результати моделювання без зашумлення
На рис. 8 представлені графіки швидкості точок крана отримані з об'єкта керування і отримані з фільтра Калмана. На графіках чітко видно, що графіки збігаються з мінімальною похибкою. Це означає що фільтр Калмана добре працює в якості спостерігача системи і дає прийнятний рівень похибки.
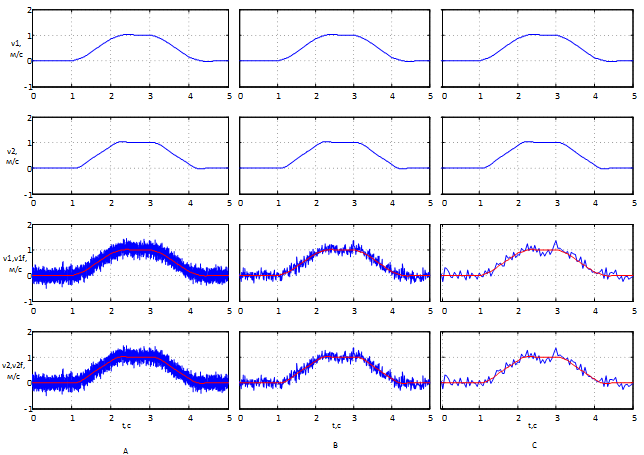
Рисунок 9 – Результати роботи з шумом при різних рівнях дискретності фільтра: А) Ts=0.001c, B) Ts=0.01c, C)Ts=0.03c
На рис. 9 представлені графіки, отримані при зашумленні сигналу зворотного зв'язку, отриманої з об'єкта керування. На графіках видно сигнал, отриманий фільтром на різних рівнях дискретності. Можна помітити, що при зниженні дискретності в даних межах результати фільтрації не погіршуються і система працює стабільно. Так само можна зробити висновок, що навіть при такому сильному зашумленні сигналу фільтр справляється зі своїм завданням, даючи системі в цілому гарну працездатність.
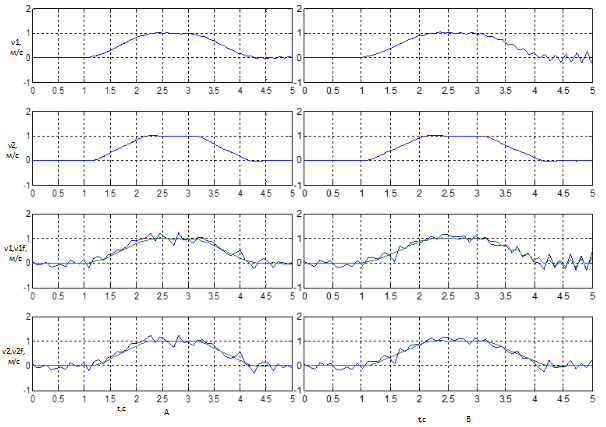
Рисунок 10 – Результати роботи з шумом при різних рівнях дискретності фільтра: А) Ts=0.009c, B) Ts=0.091c
Якщо знижувати дискретність системи до десятих секунд (рис. 10), то можна помітити, як фільтр стає не працездатним і вся система стає некерованою.
Висновки
Данна синтезована система керування з фільтром Калмана і модальним регулятором добре працює в різних частотах дискретизації і може використовуватися на слабких контролерах, але при зниженні частоти до критично низьких значень можна вивести фільтр з роботи тим самим порушивши всю систему і вивівши її з ладу.
Подальша робота буде полягати в застосуванні даної системи на реальному об'єкті, а саме на макеті мостового крана.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: червень 2018 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.
Список джерел
- Модальное управление [Електронний ресурс]. – Режим доступу: https://studopedia.ru..., вільний.
- Фильтр Калмана [Електронний ресурс]. – Режим доступу: https://ru.wikipedia.org/wiki/Фильтр_Калмана, вільний.
- Толочко О.И., Палис Ф., Бажутин Д.В. Гашение горизонтальных упругих колебаний конструкции мостового крана / О.И. Толочко, Ф. Палис, Д.В. Бажутин // Електромеханічні і енергозберігаючі системи. Тематичний випуск
Проблеми автоматизованого електропривода. Теорія і практика
- Кременчук: КрНУ, 2012. – Вип. 3/2012 (19). – С. 336-339. - Палис Ф, Толочко О.И., Бажутин Д.В. Анализ поперечных колебаний мостового крана при изменении положения тележки / Ф. Палис, О.И. Толочко, Д.В. Бажутин // Вісник Національного технічного університету
Харківський політехнічний інститут
. – Харків: НТУХПІ
, 2013, №36 (1009). – С. 36-39. - Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
- Макурин А. В., Морозов Д. И. Динамика продольного перемещения мостового крана с учетом упругости элементов конструкции // Электротехнические и компьютерные системы. – 2011. – № 3 (79). – С. 167–169.
- Бажутин Д. В. Моделирование упругих колебаний конструкций крановых установок в пакете Comsol Multiphysics. Научные работы ВНТУ, 2013, № 2
