Реферат по теме выпускной работы
Содержание
- Введение
- 1. Модальное управление
- 2. Фильтр Калмана
- 3. Описание объекта управления
- 4. Синтез системы управления
- Выводы
- Список источников
Введение
В современных системах всё чаще используются многомассовые модели. Эта работа будет проводиться на модели механизма перемещения моста мостового крана с целью гашения возникающих за счёт длинны моста упругих колебаний, которые приводят к существенным неприятностям при работе с таким механизмом. Это могут быть такие неприятные явления как раскачивание перемещаемого краном груза, что может ухудшить производственный процесс и привести к падению производительности устройства. Также немаловажным аспектом является то что при такой работе возникшие упругие колебания постепенно приводят к усталости материала и как следствие раннему выходу из строя всего механизма и таким образом повлечёт за собой остановку всего производственного процесса на время ремонта крана. В данной работе будет проведен синтез системы управления, которая могла бы устранить упругие колебания. Для управления такой системой будет использован модальный регулятор. Особенностью работы модального регулятора является то, что для функционирования ему необходим весь вектор состояния управляемой системы, но ввиду того, что непосредственно из объекта управления, зачастую, мы не можем получить все переменные состояния системы, необходимые для работы модального регулятора ввиду того что довольно часто эти величины не могут быть напрямую получены с помощью датчиков так как могут быть сложно или вообще неизмеримыми. В основном с объекта мы можем получить минимум таких переменных. Например, скорость каких-либо звеньев и ток в цепи, напряжение, подаваемое на двигатель и угол поворота вала двигателя. Для получения оставшихся переменных состояния необходимо использовать наблюдатель состояния системы, который будет синтезирован на основе математической модели объекта и сможет дать весь необходимый для работы модального регулятора вектор состояния системы. Однако сигнал, получаемый с реальных датчиков, очень часто поступает в систему управления сильно зашумлённым и тем самым может нарушить работу всей системы. Для того чтобы избежать подобных сбоев работы системы из-за шума полученного с датчиков необходимо использовать фильтр который избавил бы сигнал от шумов. В качестве такого фильтра может служить фильтр Калмана, который является очень мощным инструментом, он может не только фильтровать сигнал полученный с датчиков, основываясь на математическую модель он может предоставить весь вектор состояния системы. Таким образом используя эти два мощных инструмента вместе, мы можем реализовать систему управления без применения стороннего наблюдателя и получив при этом максимально возможно достоверные отфильтрованные показания датчиков. Также в данной работе проведены испытания полученной модели при различных уровнях дискретности системы управления и сделаны выводы по поводу работоспособности фильтра Калмана при данных изменениях.
1. Модальное управление
Суть модального регулирования заключается в корневом методе синтеза линейной САУ, то есть исходя из требуемых и желаемых показателей качества управления нужно построить желаемый характеристический полином. Это означает что нужно определить местоположение корней характеристического полинома. (В переводе с латинского, моды - это корни, отсюда и получается название регулятора - модальный регулятор).
Принцип модального регулятора заключается в расчете коэффициентов обратной связи по переменным состояния, обеспечивающих заданные показатели качества. [1]
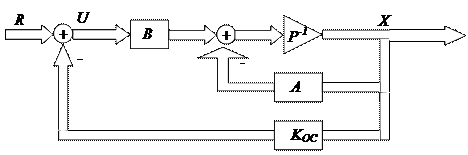
Рисунок 1 – Принцип модального регулирования
В систему нужно ввести новый вектор входных сигналов U - вектор управляющих воздействий, связь которого со старым входным вектором R обеспечивается уравнением U=R-KocX. В таком случае наша система дифференциальных уравнений, которая описывает динамику нашей системы примет следующий вид:
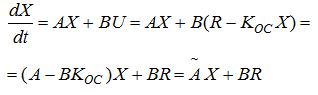
Для того чтобы синтезировать работоспособный регулятор, необходимо удостовериться что полученный нами объект является полностью управляемым и наблюдаемым.
Понятие полной управляемости подразумевает, что мы можем перевести объект из первоначального состояния в любое заданное нами положение при приложении ограниченного управляющего воздействия. Наблюдаемость, в свою очередь, это возможность по выходному вектору определить вектор состояния системы.
Для того чтобы убедиться в том, что система наблюдаема и управляема мы можем использовать критерий Калмана, который подразумевает проверку рангов матриц управляемости U и наблюдаемости V:
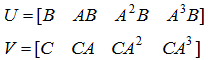
Для того чтобы считать систему полностью управляемой и наблюдаемой нам необходимо чтобы ранги матриц U и V соответствовали порядку нашей системы.
Как нам известно, динамику переходных процессов определяют корни характеристического полинома таким образом, определяя желаемый характер переходного процесса заданного полинома, возможно достигнуть необходимых для нас показателей качества.
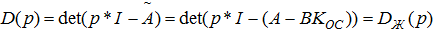
Где Dж(p) - желаемый характеристический полином, определенный исходя из заданных показателей качества регулирования по методике косвенной корневой оценки.
Таким образом далее, решая эту систему уравнений относительно неизвестных нам коэффициентов Koc можно определить необходимые для нас коэффициенты отрицательной обратной связи по вектору состояния Х, которые и будут представлять из себя модальный регулятор. Но нельзя рассчитывать на то что мы можем таким образом реализовать любой переходной процесс для любой системы просто подставив в качестве желаемых любые корни, так как в процессе создания регулятора предполагается что система линейна, что в действительности не так, и таким образом мы можем синтезировать регулятор только для этой линейной части системы.
2. Фильтр Калмана
Фильтр Калмана - эффективный рекурсивный фильтр, который оценивает вектор состояния динамической системы, используя ряды неполных и зашумленных измерений. Назван в честь Рудольфа Калмана.
Фильтр Калмана широко используется в различных инженерных и эконометрических приложениях: от радаров и систем машинного зрения до оценок параметров макроэкономических моделей. Калмановская фильтрация является важной частью теории управления, она играет огромную роль в создании систем управления. Фильтр Калмана предназначен для рекурсивного дооценивания вектора состояния изначально известной динамической системы, таким образом для того чтобы рассчитать текущее состояние системы нужно иметь текущее измерение, а также предыдущее состояние самого фильтра. Работу алгоритма можно разделить на два этапа: этап прогнозирования и этап уточнения полученного значения на основе полученного сигнала измерения. На первом этапе (этапе прогнозирования) фильтр Калмана экстраполирует значения переменных состояния, а также их неопределенности получая таким образом приблизительное значение которое может принять искомый нами сигнал. На втором этапе (этапе уточнения), по данным полученных с помощью измерения реального сигнала (полученного с некоторой погрешностью), результат первого этапа уточняется. Благодаря такой пошаговой реализации алгоритма, фильтр может отслеживать в реальном времени состояние наблюдаемого нами объекта.

Рисунок 2 – Принцип работы фильтра Калмана
На рис.2 обозначены величины:
F - матрица, которая описывает динамику системы.
B - матрица, которая определяет применение управляющего воздействия.
H - матрица которая определяет отношение между измерениями и состоянием системы.
R - матрица ковариации ошибки измерения. Её можно определить испытанием измерительных приборов и определением погрешности их показаний.
Q - матрица ковариации шума процесса. Определение шума процесса является более сложной задачей, так как требуется определить дисперсию процесса, что не всегда возможно. В любом случае, можно подобрать этот параметр для обеспечения требуемого уровня фильтрации. [2]

Рисунок 3 – Подключение фильтра Калмана
3. Описание объекта управления
Объектом управления стал механизм перемещения моста мостового крана.
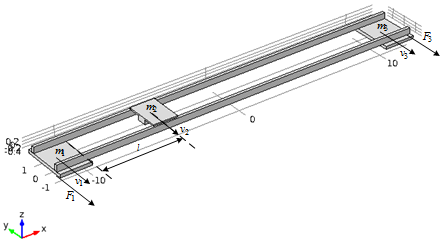
Рисунок 4 – Объект управления
Для того чтобы максимально упростить нашу модель, мост представим в виде двух цельнометаллических профилей с прямоугольным сечением и заниженными значениями плотности и модуля упругости материала так, чтобы масса конструкции примерно соответствовала реальным данным. Тележка в данном случае будет зафиксирована в одном положении и будет моделироваться как составная часть конструкции моста. Далее расположим тележку по средине моста и приложим к крайним частям нашей конструкции усилие, которое соответствует разгону моста до скорости 0.5 м/с за 1 с при отработке трапецеидального закона изменения скорости. [3]
Графики изменения скоростей крайних точек моста v1 и тележки v2, которая имеет место в его средней точке, приведены на рис.5. На данных графиках отчётливо видно, что рассматриваемые точки конструкции совершают незатухающие колебания, которые постепенно уменьшают ее прочность и в последствии могут стать причиной выхода крана из работы и травм персонала.
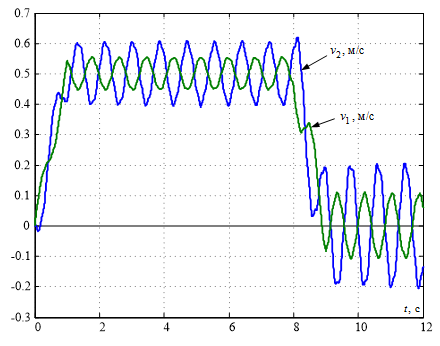
Рисунок 5 – График переходных процессов скоростей движения упругой конструкции мостового крана
Для того чтобы подавить эти незатухающие колебания необходимо синтезировать соответствующую систему управления скоростью моста, что требует наличия линейной математической модели объекта регулирования.
В нашем случае математическую модель объекта можно составить на основании кинематических схем многомассовых систем, приведенных на рис. 6.
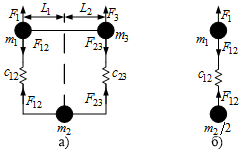
Рисунок 6 – Кинематические модели моста
На рис.6а мост условно представлен в виде трех сосредоточенных масс - крайних точек m1 и m3, связанными упругими связями с коэффициентами жесткости с12 и с23 с точкой m2, в которой находится тележка.
Если мы расположим тележку прямо посередине моста (L1=L2), то и коэффициенты жесткости упругих связей также должны быть одинаковыми. Если при таком расположении элементов равны между собой и массы, которые сосредоточены на концах моста, а также приложенные к ним силы, на одинаковом расстоянии от опор, массы которых равны, то кинематическую схему нашего объекта управления можно упростить до двухмассовой, оставив одну опору и центральную точку, массу которой следует уменьшить в 2 раза. Кинематическая схема для такого случая представлена на рис.6б. Ее математическое описание будет иметь такой вид:
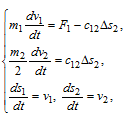
где F1 - сила, которую прилагают к первой массе, F12 - упругая сила, Δs2=s1-s2 - величина упругой деформации.
Если мы знаем значения сосредоточенных масс и постоянной времени упругих колебаний двухмассовой системы T12=1/2/pi/f, то мы сможем рассчитать коэффициент жесткости: [3]
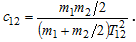
Где:
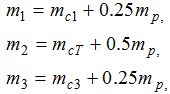
Таким образом, введя некоторые допущения и упрощения мы преобразовали сложную трёхмассовую кинематическую систему в более простую двухмассовую модель, на которой будет намного легче проводить опыты и реализовывать систему управления с целью гашения вредных для объекта упругих колебаний.
4. Синтез системы управления
Одним из способов гашения данных колебаний является использование модального регулятора. Для того чтобы синтезировать данный регулятор необходимо перевести нашу систему в пространство состояний, для этого необходимо преобразовать данные уравнения в матрицы пространства состояния:
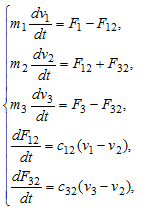
Вектор входных сигналов равен
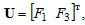
Вектор переменных состояния
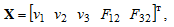
Матрица состояния А равна:
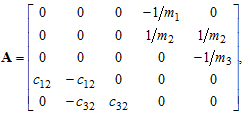
Входная матрица В равна:
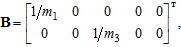
В пакете Simulink была синтезирована модель, включающая объект управления в пространстве состояний, модальный регулятор и фильтр Калмана (рис.7)
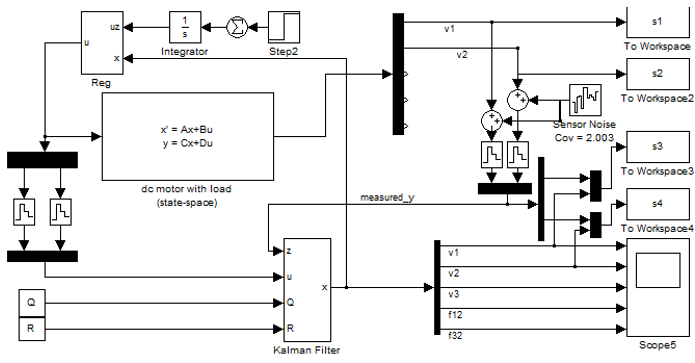
Рисунок 7 – Модель для испытаний
На данной модели расположены такие элементы как модель объекта в пространстве состояния, которая основана на матрицах состояния нашего объекта управления (state-space), модальный регулятор (Reg) реализованный как отрицательная обратная связь по вектору состояния объекта который получен из выхода фильтра Калмана (Kalman Filter), на вход которого подаются зашумлённые сигналы скорости с объекта управления, а также управляющее воздействие как и на объект управления, но с дискретизацией сигнала по уровня, чтобы имитировать дискретную систему управления, блоки дискретизации и вывода данных в рабочее пространство Matlab для получения графиков переходных процессов. Также можно увидеть блок Step и Integrator выполняющие функцию задания трапецеидального закона управления.
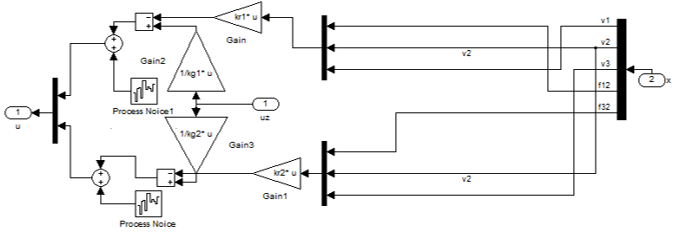
Рисунок 8 – Содержимое блока Reg
В блоке Reg расположены такие объекты как коэффициенты обратной связи, которые являются модальным регулятором и блоки Process Noise которые вносит в систему управления погрешность, выражающую неточность описания модели объекта, которую в общем случае нельзя вычислить, но можно подобрать, добившись максимально качественных результатов.
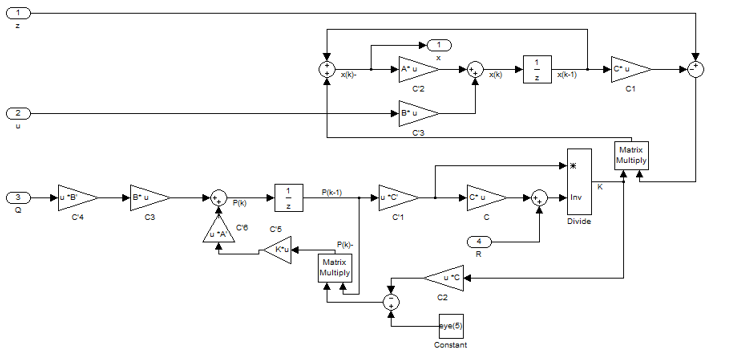
Рисунок 9 – Содержимое блока Kalman Filter
На рисунке 9 представлено содержимое фильтра Калмана, где на вход подаются такие сигналы как управляющее воздействие, зашумлённые сигналы снятые с объекта управления и зашумлены, с целью имитации работы реального датчика, также на вход фильтра подаются величины, характеризующие ковариацию шума датчика и системы. Ковариация датчика может быть получена опытным путём по выборке сигнала с реального датчика. Ковариация модели не может быть получена таким образом и подбирается вручную.
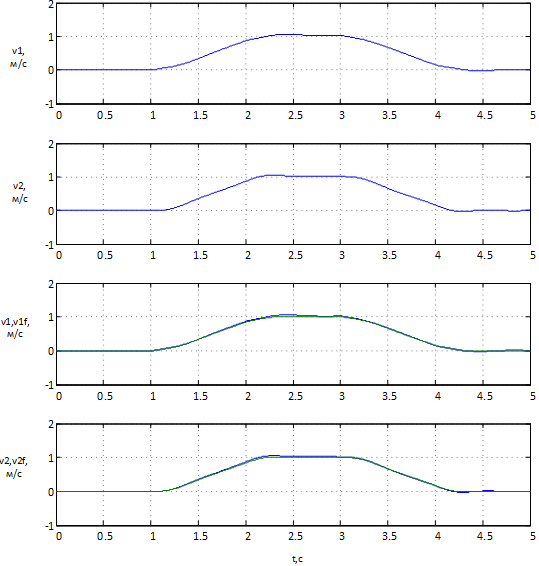
Рисунок 10 – Результаты моделирования без зашумления
На рисунке 10 представлены графики скорости точек крана полученные с объекта управления и полученные с фильтра Калмана, на графиках отчётливо видно, что графики совпадают с минимальной погрешностью. Это означает что фильтр Калмана хорошо работает в качестве наблюдателя системы и даёт приемлемый уровень погрешности.
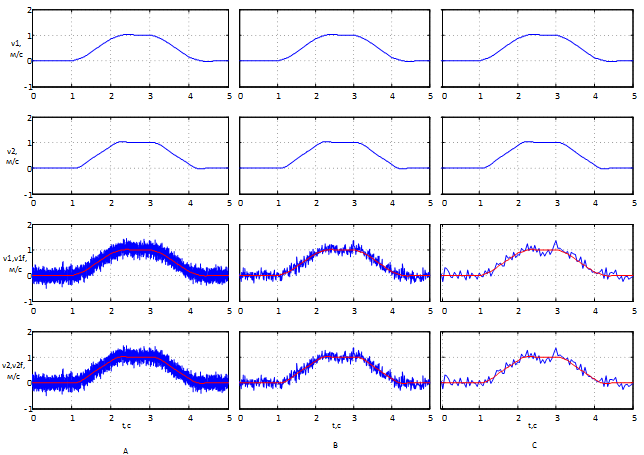
Рисунок 11 – Результаты работы с шумом при различных уровнях дискретности фильтра: А) Ts=0.001c, B) Ts=0.01c, C) Ts=0.05c
На рисунке 11 представлены графики, полученные при зашумлении сигнала обратной связи, полученной из объекта управления. На графиках видно сигнал получаемый фильтром на различных уровнях дискретности. Можно заметить, что при понижении дискретности в данных пределах результаты фильтрации не ухудшаются, и система работает стабильно. Также можно сделать вывод что даже при таком сильном зашумлении сигнала фильтр справляется со своей задачей давая системе в целом хорошую работоспособность.
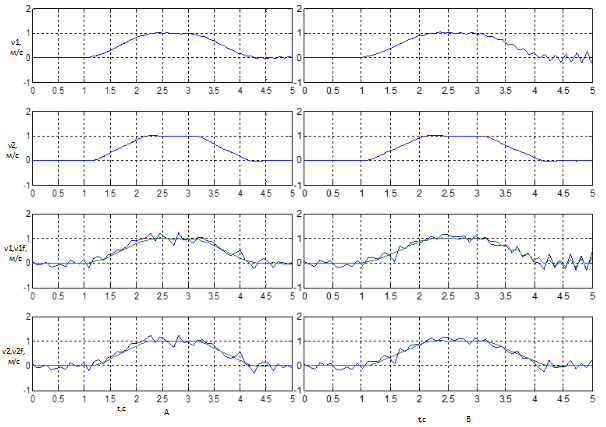
Рисунок 12 – Результаты работы с шумом при различных уровнях дискретности системы: А) Ts=0.009c, B) Ts=0.091c
Если понижать дискретность системы до десятых секунды (рис.12), то можно заметить, как фильтр перестаёт корректно работать, и вся система становится неуправляема.
Выводы
Данная синтезированная система управления с фильтром Калмана и модальным регулятором хорошо работает в различных частотах дискретизации и может использоваться на слабых контроллерах, но при понижении частоты до критически низких значений можно вывести фильтр из работы тем самым нарушив всю систему и выведя её из строя.
Дальнейшая работа будет заключатся в дальнейшем применении данной системе на реальном объекте, а именно на макете мостового крана.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2018 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Модальное управление [Электронный ресурс]. – Режим доступа: https://studopedia.ru..., свободный.
- Фильтр Калмана [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Фильтр_Калмана, свободный.
- Толочко О.И., Палис Ф., Бажутин Д.В. Гашение горизонтальных упругих колебаний конструкции мостового крана / О.И. Толочко, Ф. Палис, Д.В. Бажутин // Електромеханічні і енергозберігаючі системи. Тематичний випуск «Проблеми автоматизованого електропривода. Теорія і практика» - Кременчук: КрНУ, 2012. – Вип. 3/2012 (19). – С. 336-339.
- Палис Ф, Толочко О.И., Бажутин Д.В. Анализ поперечных колебаний мостового крана при изменении положения тележки / Ф. Палис, О.И. Толочко, Д.В. Бажутин // Вісник Національного технічного університету «Харківський політехнічний інститут». – Харків: НТУ «ХПІ», 2013, №36 (1009). – С. 36-39.
- Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. – СПб.: Энергоатомиздат, 1992. – 288 с.
- Макурин А. В., Морозов Д. И. Динамика продольного перемещения мостового крана с учетом упругости элементов конструкции // Электротехнические и компьютерные системы. – 2011. – № 3 (79). – С. 167–169.
- Бажутин Д. В. Моделирование упругих колебаний конструкций крановых установок в пакете Comsol Multiphysics. Научные работы ВНТУ, 2013, № 4
