Авторы: Баранов А. М., Осипов Е. В.
Источник: Сборник статей магистрантов. Выпуск V. – Тамбов: ТОГУП
Тамбовполиграфиздат
, 2006. – 115-118 с.
В настоящее время актуальна задача оптимального управления энергоемкими объектами. Существует множество подходов к решению задач такого рода - это применение различных систем оптимального управления (СОУ) с использованием простых, линейно-квадратичных или энергосберегающих регуляторов.
Однако, при применении различных СОУ, возникает проблема, связанная с появлением шумов измерения на выходе объекта управления, что приводит к значительному снижению эффективности системы. Решить указанную проблему позволяет применение различных фильтров. Наиболее широкое применение получил фильтр Калмана.
Для дискретного случая в общем виде предполагается заданной следующая модель объекта управления:
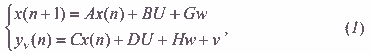
Первое уравнение системы – уравнение состояния, второе – уравнение наблюдений, где x – фазовая переменная, y – измеренное ее значение.
Известны входное воздействие U и возмущения на входе w и измерения v, которые являются «белым шумом» со следующими характеристиками:
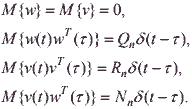
Синтез наблюдателя для оценивания вектора переменных состоя- ния объекта проводится исходя из минимизации установившейся ошиб- ки оценивания:
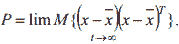
Оптимальным решением является фильтр Калмана описываемый уравнениями:

где матрица коэффициентов обратной связей L определяется на основе решения уравнения Рикатти [1].
На рисунке 1 показана структурная схема СОУ с использованием фильтра Калмана.
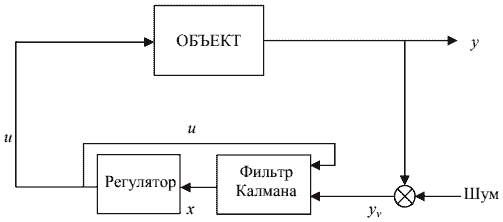
Рисунок 1 – Структурная схема СОУ с применением фильтра Калмана
В данной статье рассматривается применение фильтра Калмана с целью обеспечения устойчивости СОУ к воздействию помех. В качестве объекта управления рассматривается технологическая установка термообработки магнитопроводов ТОМ-1
Объект управления принадлежит классу электрических печей сопротивления, в которых электрическая энергия превращается в тепло в твердых или жидких телах при протекании через них тока.
Погрешности измерительных приборов – основные источники помех, влияющие на точность управления.
Рассмотрим процесс синтеза фильтра Калмана с использованием MatLab. В результате идентификации экспериментальных данных получена модель объекта в дискретном виде – двойной интегратор:
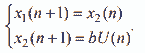
Шаг дискретизации Δt = 0,1с.
Параметры модели следующие: a = 1, b = 0.2,
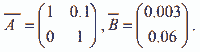
Значения весовых коэффициентов:

Этапы синтеза фильтра Калмана на основе исходных данных следующие:
1. Задаем исходные данные (модель ДИ-звено):
a=[0 0.1; 0 1], b=[0.003;0.06], с=[1 0], q=[1 1;1 7], r=1.
2. Рассчитываем матрицу коэффициентов обратной связи: [k,s,e] = dlqr(a,b,q,r)
В результате расчета получаем:

3. Задаем исходные данные для расчета фильтра Калмана: qn=7 – ошибка измерения, rn=1 – возмущение, nn=0, sys=ss(a,b,c,0,0.1).
Синтезируем переменную Kest при помощи функции Kalman:
[kest,L,P,M,Z] = kalman(sys,qn,rn,nn);
Kest – ss-модель фильтра Калмана,
L и P – матрицы приведенного вида,
М – обновленная матрица обратной связи,
Z – ковариационная матрица оценивания ошибок в установившемся режиме.
В результате получаем:

Окончательный вид фильтра можно получить, подставив данные коэффициенты в выражение (2).
В результате проведенной работы был синтезирован фильтр Калмана для заданного объекта управления, что позволило существенно повысить точность управления.
1. Дъяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. – Спб.: Питер, 2002г. – 448 с.