Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель исследования
- 3. Обзор исследований и разработок
- Выводы
- Список источников
Введение
Магнитные явления были известны ещё в древнем мире: компас был изобретён более 4000 лет назад, и к XII веку он стал известен в Европе. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом, и возникло представление о магнитном поле. Первыми экспериментами, показавшими, что между электрическими и магнитными явлениями имеется связь, были опыты датского физика Х. Эрстеда (1777-1851). В своём знаменитом опыте, описываемом ныне во всех школьных учебниках физики и проведённом в 1820 году, он обнаружил, что провод, по которому идёт ток, действует на магнитную стрелку
Эрстед не только провёл свой опыт, но и сделал правильный вывод, что электрический конфликт не ограничен проводящей проволокой, а имеет довольно обширную сферу активности вокруг этой проволоки. Это можно понимать, как действие тока есть не только внутри провода, но и вокруг него.
1. Актуальность темы
Организм человека подвержен влиянию внешней среды: перепадами давления, фазам луны, затмению, радиацией, магнитные поля которые создают трансформаторы. Повседневно в металлургии используются всевозможные печи, которые излучают поля влияющие на организм человека. Для безопасной работы необходимо знать угрозу создаваемую установкой, которую обслуживает персонал и обезопасить их от негативного воздействия на их организм.
2. Цель исследования
Целью исследование является поле создаваемое промышленной вакуумной печью СНВЭ
- Снять реальные параметры с вакуумной установки.
- Построить модель по полученным данным в программном обеспечении.
- Сравнить результаты обычной установки и экранированной.
3. Обзор исследований
Неподвижный электрический заряд и неподвижный магнитный полюс не взаимодействуют друг с другом. Между ними нет ни силы притяжения, ни силы отталкивания, и эти силы не возникают между ними ни при каких обстоятельствах, если они остаются неподвижными друг относительно друга. Однако достаточно привести электрический заряд или магнитный полюс в движение, как тотчас между ними появляется сила взаимодействия, стремящаяся вращать их друг относительно друга. Сила эта возрастает при увеличений скорости их относительного движения и, помимо того, зависит от угла, образуемого направлениями их движения. При движении зарядов и при перемещении связанного с зарядами электрического поля возникает магнитное поле. Вокруг движущегося электрического заряда появляются замкнутые линии магнитных сил; линии эти в виде концентрических окружностей охватывают траекторию заряда. Когда по проводнику проходит ток, вокруг проводника образуются замкнутые линии магнитной индукции, концентрическими кольцами охватывающие проводник: магнитные силы во всех точках плоскости, перпендикулярной к оси прямого тока, направлены по касательной к окружности, проведенной из точки пересечения оси тока с плоскостью, и лежат в этой плоскости. Силы, действующие в магнитном поле тока, убывают с увеличением расстояния от оси тока. Направление магнитного поля связано с направлением тока правилом буравчика: Если поступательное движение винта означает направление тока в проводе, то направление вращения ручки буравчика будет соответствовать направлению линий магнитного поля. При поступательном движении буравчика в направлении тока вращательное движение рукоятки буравчика указывает направление силовых линий магнитного поля тока. Правилом буравчика можно пользоваться также для определения направления тока по направлению его магнитных силовых линий. Если ввинчивать буравчик по направлению магнитной линии, то направление поворота ручки укажет направление тока в контуре, охватывающем эту силовую линию. Наряду с правилом буравчика часто пользуются также следующим правилом: если смотреть по направлению тока, то магнитные линии будут направлены в сторону движения стрелки часов. Вид магнитного поля в пространстве для случая прямолинейного тока может быть представлен как ряд коаксиальных цилиндрических поверхностей, имеющих своей осью ось тока. Магнитные силы в поле прямого тока в любой его точке всегда направлены по касательным к цилиндрической поверхности, проходящей через эту точку, и перпендикулярны к образующей, на которой лежит данная точка [1].
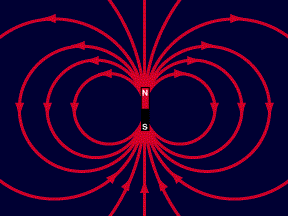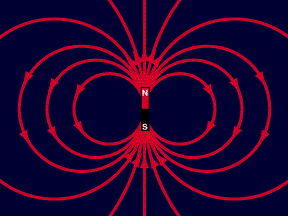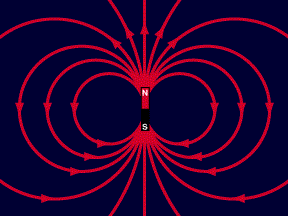
Рисунок 1 – магнитное поле.
Рассмотрим поле постоянных токов в диэлектрической среде. Как в самой среде, окружающем проводники с постоянным током, так и в внутри проводников существуют магнитное и электрическое поля. Эти поля стационарны. Вне источника ЭДС электрическое поле постоянных токов является, так же как и электростатическое поле, безвихревым. Такое поле является потенциальным, т.е. для его характеристики может быть введена функция координат. Таким образом, электрическое поле в диэлектрической среде, окружающем проводники с постоянными токами [2]. Итак, в диэлектрической среде такое поле ничем не отличается от электростатического, но граничные условия на поверхности проводников уже не соответствуют тем, которые имеют место в электростатике. В электростатической задаче поверхность каждого проводника является поверхностью равного потенциала. При протекании постоянного тока в проводнике возникает падение потенциала, а значит, поверхность проводника уже не будет равно потенциальной. Так как на поверхности проводника появляется касательная составляющая напряженности поля в направлении линий тока, линии напряженности электрического поля в диэлектрической среде подходят к поверхности проводника не под прямым углом. Данное обстоятельство значительно осложняет расчет поля, тем не менее, практически во всех случаях его можно не учитывать, поскольку обычно падение напряжения вдоль проводников на длине, сравнимой с расстоянием между проводниками, ничтожно мало по сравнению с разностью потенциалов проводников. При рассмотрении поля около проводов ею можно пренебречь без опасения внести этим какую-нибудь заметную ошибку. В таком случае граничные условия на поверхности проводников оказываются тождественными условиям в электростатике. Поэтому при рассмотрении электрического поля в диэлектрической среде, окружающей проводники с постоянными токами, можно использовать решения, полученные при рассмотрении соответствующих электростатических задач.
Рассмотрим теперь электромагнитные процессы, сопровождающие атмосферный разряд, например, удар молнии в молниеотвод. При этом, как правило, необходимо учитывать неоднородность электрических свойств среды, а также их изменение. При математическом моделировании исследуемых процессов могут изменяться также геометрическая конфигурация или электрические параметры исследуемой разрядной структуры. Заметим, что как высота молниеотвода, так и длина фидерного канала молнии на несколько порядков превышает их диаметр. Поэтому при использовании метода конечных разностей шаг пространственной сетки h обычно выбирается значительно больше радиуса r0 , например, равным средней длине шага при росте разрядной структуры (молнии). В соответствии с методом конечных разностей исследуемая область с тонкой проводящей проволокой, разбивается на ячейки так, что узлы расчетной сетки лежат на границах раздела сред и на оси проволоки. В пределах каждой из ячеек, кроме тех, которые примыкают к проволоке, свойства диэлектрической среды полагаются однородными [3]. Задание электрических свойств среды осуществляется путем присвоения значений относительной диэлектрической проницаемости и удельной электропроводности ячейкам расчетной схемы. Граничные условия зависят от вида поле образующей системы. Записав уравнения для каждого узла расчетной сетки в разностном виде как и граничные условия, получаем систему уравнений, которую автор предлагает решать итерационным методом. Для учета присутствия в расчетной области тонкой проволоки длиной введем систему, в которой в частности проволока расположена вдоль оси Y перпендикулярно земле и одним концом касается ее поверхности. Коэффициенты компонент тензора узлов, расположенных на Перейдем к рассмотрению системы коронирующих проводов над заземленной поверхностью. Для расчета электрических полей и зарядов, возникающих в данной системе в работе используется система уравнений Максвелла, описывающая распределение электрического поля и заряда: Граничные условия: а) на поверхности проводов задается постоянный потенциал; б) на поверхности земли потенциал постоянен и равен нулю; в) в случае возникновения короны, на проводе всегда устанавливается одно и то же значение нормальной составляющей напряженности электрического поля, для которого известна эмпирическая формула Пика [4]. В соответствии с этими предположениями система распадается на две независимые системы уравнений. Уравнения начального приближения: где — невозмущенный потенциал. По уравнениям определяется поле в отсутствии короны. Для ставятся обычные граничные условия для потенциала на земле и проводах. Обратим в этой связи внимание и еще на одну особенность — отсутствие граничного условия для ?, что не вызывает трудностей в частных случаях, когда аналитическое решение задачи возможно, но при численном решении данное обстоятельство существенно усложняет алгоритм расчета. В указанные трудности предлагается преодолеть введением новой функции ?: Причем на поверхности земли. Решая уравнение от поверхности земли, получаем значение ?????a на поверхности провода. Плотность заряда вдоль силовой линии: Зная плотность заряда, можно найти функцию ? вдоль силовой линии, решая уравнение от поверхности провода. Таким образом, исходя из приведенных математических моделей, исследование электрических полей может быть проведено на базе решения внешней краевой задачи для уравнения Лапласа с граничными условиями Дирихле и Неймана.
Для внешних краевых задач существует узкий круг аналитических решений в случае простого описания геометрии тел. Например, для канонических областей применяется метод конформных отображений, т.е. сводится внешняя задача к внутренней. Однако в общем случае для сложной области затруднено построение отображающей функции. Применение численных методов для решения внешних краевых задач ограничено, поскольку граничные условия ставятся непосредственно на бесконечности, а расчетная область, как и число узлов в сетке, берется конечной, это ограничивает применение сеточных методов к таким задачам. В существующих программных комплексах при решении внешних краевых задач обычно используются сеточные методы. Обеспечение высокой точности, при одновременном ограничении на допустимые объем вычислений и памяти — это одно из основных требований, предъявляемых к численным моделям. Характеристические граничные условия являются самым простым, а, следовательно, и наиболее широко используемым способом моделирования граничных условий, однако они чаще всего не удовлетворяют требованиям по точности. Явный способ улучшения точности — расширение области расчета — в большинстве случаев приводит к чрезмерным затратам по памяти и количеству операций.
Методы, отвечающие требованиям по скорости, точности и широте класса рассматриваемых задач, входят в интенсивно развивающийся круг тем [5]. Моделирование плоских электрических полей с помощью аналоговых вычислительных машин осуществляется на установках, выполненных из фольги или электропроводной бумаги, для моделирования же объемных полей использовались сеточные интеграторы или электролитический бак. Остановимся подробнее на моделирующем устройстве, применяемым Г. А. Рязановым, для моделирования бесконечно протяженных плоских полей, аналогом которого является устройство, предложенное Л. В. Ницецким и А. Ф. Фокиным [6].
Ключевая идея предлагаемого подхода предельно ясна. При решении внешней краевой задачи внешних границ не существует и в бесконечности вектор E стремится к нулю, поэтому поле определяется граничными условиями на поверхностях, ограничивающих данную область изнутри. При моделировании подобного поля проводящий слой не должен иметь свободных границ, на которых могут возникать стационарные заряды. Помимо этого, электроды не должны искажать строение поля в рабочей области модели, если общий линейный поток вектора E через внутренние контуры отличен от нуля (ток отводится с помощью внешних электродов). Если общий линейный поток вектора E через внутренние контуры равен нулю, то внешняя шина, наклеенная по периметру листов электропроводной бумаги, оставляется изолированной от цепи. Внутренние границы поля должны быть расположены в средней части листа, для того чтобы влияние его внешних границ было бы незначительным [7]. Таким образом, модель состоит из двух круглых листов электропроводной бумаги, изолированных друг от друга картоном или листом обыкновенной бумаги. Края можно склеить электропроводным клеем или соединить между собой дискретным способом с помощью гвоздиков. «Рабочим является верхний лист — на нем устанавливают электроды, с помощью которых реализуются граничные условия на внутренних контурах области поля, а нижний лист устраняет влияние краев верхнего листа.» В этом случае проводящий слой оказывается замкнутым и лишенным свободных краев; строение поля остается невозмущенным на всей поверхности верхнего листа. Силовые линии пересекают края верхнего листа и замыкаются через нижний лист, который заменяет отсутствующую бесконечно протяженную внешнюю область проводящего слоя. Стационарное электрическое поле в нижнем листе (являясь конформным отображением поля во внешней области) замыкает поле, существующее в верхнем листе... При этом всем бесконечно удаленным точкам соответствует центр нижнего листа». Поэтому там лучше всего установить электрод, отводящий ток из модели.
Модель представляет собой полукруг или квадрант, если поле имеет линии симметрии. При совпадении силовой линии с линией симметрии, соответствующие края нижнего и верхнего листов остаются свободными; если же линия симметрии является изопотенциальной линией, то вдоль краев обоих листов наклеивается сплошная полоска фольги [8]. М. И. Дыльков продолжил исследование двойных моделей, описанных в работе Г. А. Рязанова, но уже численными методами и предложил метод инверсии бесконечной области для решения плоских и объемных внешних краевых задач для уравнений эллиптического типа второго порядка, который основан на отображении ее на дополнительную расчетную область с заданием граничного условия на бесконечности в центре этой области. Поясним, нижний и верхний листы называются в дополнительной и основной областями соответственно. В работе указывается, что «…при описании метода аналогового моделирования с помощью электропроводной бумаги, области можно было соединять как непрерывно, склеивая по краям электропроводящим клеем, так и дискретно, с помощью игл. В данном случае, предлагаемое в методе инверсии бесконечной области соединение моделирует именно последний, дискретный вариант», т.е. «…основная и дополнительная области оказываются как бы склеенными по границам». Метод был опробован на плоской и объемной внешних краевых задачах (для бесконечно длинного провода и точечного заряда). Отметим еще и тот факт, что «несмотря на то, что …расчет выполняется по всем узлам, сравнение будет производиться только по основным расчетным областям…» как и в, где, как известно, рабочей областью модели является только верхний лист. В предполагается, что основная и дополнительная области имеют форму квадрата в двумерном случае или куба в трехмерном случае. Для упрощения программной реализации было принято установить признаки граничных узлов по прямым — сторонам квадратных расчетных областей,— или же по плоскостям — граням кубических расчетных областей. При этом отмечается, что данное упрощение повлияет на точность получения решения задачи в углах расчетной области, т.е. проявятся краевые эффекты [9]. Итак, вышеизложенный метод инверсии бесконечной области, позволяющий достаточно просто сводить внешние задачи к задачам в ограниченных областях, и внутренние задачи решать методом сеток, снимает ограничения по применению сеточных методов к классу внешних краевых задач и позволяет использовать точные граничные условия на бесконечности, в общем случае для двумерных и трехмерных областей. Помимо этого он обладает относительной простотой реализации алгоритма в условиях исследуемых задач и геометрической универсальностью, допускает произвольный выбор сетки при построении разностных задач, который вытекает из требования более точного представления граничных поверхностей, предъявляемого к решению каждой конкретной задачи. Описанный подход не в полной мере разработан для исследуемых задач, не рассматривались краевые задачи в полупространстве с однородными или неоднородными условиями первого, второго или третьего рода на полу бесконечных и бесконечных границах [10].
Выводы
В работе был рассмотрен комплекс проблем, связанных с математическим моделированием электрических полей. Развит метод инверсии, используемый при решении внешних краевых задач с граничными условиями Дирихле и Неймана в двумерном и трехмерном полупространстве. Обосновано использование значений в точках обеих частей двусоставной области при анализе результатов решения. Разработаны вычислительные алгоритмы и создано на их основе программное обеспечение для моделирования электрических полей на основе метода инверсии. Произведенные тестовые расчеты показали, что разработанные алгоритмы сокращают требуемый объем вычислительных ресурсов. Обнаружено существенное увеличение точности тестовых расчетов согласно развиваемому методу инверсии по сравнению с подходами, использующими обычные характеристические граничные условия. Помимо этого, компьютерное моделирование электрических полей с применением развиваемого метода инверсии адекватно результатам вычислительного и натурного экспериментов, проведенных другими авторами, качественно и количественно. В отличие от ранее выполненных работ сходной тематики в данном научном исследовании решаются внешние краевые задачи в двумерном и трехмерном полупространстве с заданием граничных условий как на замкнутых, так и на полу бесконечных и бесконечных поверхностях в соответствии с методом инверсии, учитывающем значения в обеих частях двусоставной области и повышающем быстродействие решения подобного класса задач при моделировании электрических полей.
Список источников
- Калашников С.Г. Электричество: Учебное пособие. –М.: Наука. 1985. –576с.
- Теоретические основы электротехники : В 3-х т. Том 3. – 4-е изд. / К. С. Демирчян, Л. Р. Нейман, В. Коровкин, В. Л. Чечурин. – СПб. : Питер, 2004 г. – 377 с.
- Потапенко, А. Н. Математическая модель и численный метод исследования электрических полей высоковольтных воздушных линий электропередач / А. Н. Потапенко, Е. А. Канунникова, О. В. Донева // Известия высших учебных заведений. Северо-Кавказский регион. Технические науки. – 2008. – № 5. – С. 41-45.
- Попков, В. И. Коронный разряд и линии сверхвысокого напряжения : избранные труды / В. И. Попков. – М. : Наука, 1990. – 256 с.
- Рязанов, Г. А. Опыты и моделирование при изучении электромагнитного поля / Г. А. Рязанов. – М. : Наука, 1966. – 191 с.
- Канунникова, Е. А. Метод инверсии внешней бесконечной области применительно к задачам электростатики / Е. А. Канунникова // Образование, наука, производство и управление : сб. докл. междунар. науч.-практич. конф. 22–23 ноября 2007 г. – Ст. Оскол : Изд-во СТИ, 2007. – С. 101-104.
- Свешников, А. Г. Лекции по математической физике /А. Г. Свешников А. Н. Боголюбов, В. В. Кравцов. – М.: Изд-во МГУ, 1993. – 352 с.
- Колечицкий, Е. С. Расчет электрических полей устройств высокого напряжения / Е. С. Колечицкий. – М. : Энергоатомиздат, 1983. – 168 с.
- Yang, Y. The strip simulation method for computing electric field on conductor surfaces / Y. Yang, D. Dallaire, J. Ma, F. P. Dawalibi // Power and Energy Systems (EuroPES 2003) : proceedings of the Third IASTED International Conference 3-5 sept. 2003, Marbella. – 2003. – P. 353-357.
- Справочная книга радиолюбителя–конструктора/ А.А. Бокуняев, Н.М. Борисов, Р.Г. Варламов и др. Под ред. Н.И. Чистякова. – М.: Радио и связь, 1990. - 624 с.
