Реферат по теме выпускной работы
Разработка и исследование устройств циклического кодирования
Содержание
- Введение
- 1. Актуальность и мотивация
- 2. Цели и задачи
- 3. Обзор исследований и разработок по теме
- 4. Методы исследований
- 5. Научная новизна
- 6. Планируемые практические результаты
- 7. Апробация работы
- 8. Содержание работы
- Заключение
- Список источников
Введение
Происходящие в последние десятилетия динамичные изменения в различных сферах деятельности общества характеризуются лавинообразным ростом объемов самой различной информации: социально – политической, производственной, научной, культурной и др. Международная практика показывает, что информационный потенциал в обществе начинает все больше определять его экономический потенциал наравне с материальным производством. Экономическое развитие такого общества будет целиком определяться результатами интеллектуальной деятельности. Это связано с возрастающей ролью информации, которая становится определяющей в развитии различных сфер деятельности общества.
1. Актуальность и мотивация
Признанный классик теории постиндустриализма Д. Белл выделяет три технологических революции: изобретение паровой машины в XVIII веке; научно-технологические достижения в области электричества и химии в XIX веке; создание компьютеров в XX веке [1].
Современная цивилизация XXI века переживает очередную революцию – информационную. Стремительные темпы разрастания всемирной паутины приводят к формированию цифровой цивилизации: если в 2000 году было 359 млн. пользователей сети Интернет, то в марте 2017 года количество пользователей уже 3732 млн. – это половина населения земного шара. В средствах массовой информации все чаще объявляют грядущую (а некоторые – уже наступившую) зеттабайтную эпоху развития человечества. По оптимистическим прогнозам – в период с 2012 по 2020 годы ежегодно будет происходить удвоение объема данных и на конец этого периода он составит примерно 37 ЗБ [2].
Достоинства информизации и роботизации трудно переоценить. В последние десятилетия достижения в области внедрения информационных технологий являются одним из определяющих факторов экономического потенциала общества. В результате появляется и развивается информационная инфраструктура, которая предоставляет новые услуги, такие как дистанционное образование, телеработа, телемедицина, электронная торговля, заказ билетов для транспорта, интернет-банкинг, оплата счетов, и др. Вместе с тем, увеличение количества информации, которая передается, хранится и обрабатывается, приводит к требованиям обеспечения ее достоверности и надежности используемых аппаратных и программных средств. От успешного решения этих задач, с одной стороны, зависит процветание нынешней цивилизации, или, с другой стороны – ее саморазрушение, например, из-за случайного или намеренного сбоя в военных приложениях. Кроме того, необходимо учитывать такие явления, как солнечная активность и жесткое космическое излучение.
Уменьшение топологических норм проектирования СБИС памяти увеличивает чувствительность ИС к локальным радиационным эффектам. При этом может не просто увеличиваться количество ошибок, но и меняться их характер. При этом задача повышения отказоустойчивости памяти с помощью помехоустойчивых кодов становится особенно актуальной [3].
Поэтому для устранения возможных ошибок из-за естественных природных явлений, либо искусственных причин, или дефектов аппаратных информационных средств, для защиты от разрушений, возникающих под действием жесткого космического излучения, используются современные технологии помехоустойчивого кодирования при проектировании микросхем памяти, весь спектр методов и средств встроенного самотестирования цифровых систем [1-22].
2. Цели и задачи
Целью работы является разработка методов циклического кодирования, новых методов компактного тестирования, исследование их достоверности, а также разработка схем, реализующих эти методы.
Исследования велись в следующих направлениях.
- Разработка альтернативных методов циклического кодирования, а также аппаратной реализации кодирующих и декодирующих устройств.
- Разработка альтернативных методов компактного тестирования на основе методов циклического кодирования.
- Экспериментальная верификация полученных теоретических результатов с помощью средств САПР Active‐HDL.
3. Обзор исследований и разработок по теме
Применение принципов псевдослучайного тестирования позволило эффективно диагностировать типовые элементы замены (ТЭЗ) и модули серийно выпускаемых в СССР ЭВМ серии ЕС, таких как: ЕС-1036, ЕС-1061, ЕС-1130, ЕС-1842 и др. Высокая эффективность компактного тестирования с использованием псевдослучайных тестовых воздействий и синтезированных генераторов псевдослучайных исчерпывающих тестов позволила применить его для реализации тестирования всех типовых элементов замены ЭВМ ЕС-1130. [4]
Анализ диагностического обеспечения микропроцессорных СБИС ведущих зарубежных фирм: IBM (S/390, метод LSSD); Hewlett Packard (сигнатурный анализ); альянс компаний Apple, IBM и Motorola (Power PC); Motorola (MC 202-206); Intel Corporation (микропроцессоры 80386, Pentium Pro); Advanced Micro Devices (AMD-K6), показывает, что 5-8 % площади кристалла СБИС занимают встроенные схемы тестирования, которые позволяют обнаружить практически 100% дефектов. Например, диагностическое обеспечение микропроцессора S/390 включает: ОЗУ, кэш, память, схемы их управления со встроенными схемами самотестирования; триггеры, регистровые сети, образующие в режиме тестирования сканируемый путь по методу LSSD; встроенные ГТП; встроенный АТР - многоканальный сигнатурный анализатор; порт JTAG в соответствии со стандартом IEEE 1149.1.
Методы исчерпывающего тестирования КС и сканирования позволяют вместе обнаруживать 95% неисправностей. Применение разных псевдослучайных последовательностей, обеспечивает 99,9 % покрытия всех неисправностей СБИС.
4. Методы исследований
При выполнении работы использовался математический аппарат булевой алгебры, аппарат технической диагностики, теории полей Галуа, теории и практики помехоустойчивого кодирования, теории сигнатурного анализа и теории матриц. Проверка работоспособности предлагаемых методов и аппаратных средств, их реализующих, проводилась с помощью компьютерного моделирования, в частности, с применением САПР Active-HDL.
5. Научная новизна
Научная новизна работы заключается в разработке новых методов компактного тестирования и их схемной реализации, а также решении различных задач вычисления достоверности контроля с их помощью и с помощью систем на основе известных методов встроенного тестирования. В частности, предложены.
I Альтернативные методы циклического кодирования и аппаратной реализации кодирующих и декодирующих устройств.
- Варианты аппаратной реализации кодов БЧХ и Рида-Соломона, исправляющих одиночные и двойные ошибки (пакетов ошибок) и использующих синдромный метод декодирования. В отличие от типичного декодера не требуется блоков решения ключевого уравнения на основе одного из алгоритмов, (например, Берлекэмпа-Месси, алгоритма Евклида или Питерсона-Горенcтейна-Цирлера), поиска корней полиномов локаторов ошибок на основе алгоритма Ченя, расчета значения ошибки (алгоритм Форни).
- Метод укорачивания и аппаратная реализация циклических кодов на основе двойственных полиномов. В отличие от известных методов позволяет укорачивать коды с большим параметром укорачивания.
- Альтернативный метод деления полиномов. В отличие от известных методов позволяет деление полиномов большой степени.
- Метод укорачивания и аппаратная реализация циклических кодов на основе альтернативного деления полиномов. В отличие от известных методов позволяет укорачивать коды большой длины и применение известных методов декодирования.
II Альтернативные методы компактного тестирования на основе методов циклического кодирования
- Метод аналитического вычисления сигнатур. В отличие о известных использует степенную форму компактных оценок, что позволяет упростить определение сигнатур.
- Определение параметра тестируемости комбинационных схем. На его основе сформулировано и доказано условие равенства нулю сигнатур для конъюнкций определенного ранга. Рассмотрены следующие варианты.
- Для порождающих полиномов регистров сдвига с линейными обратными связями (РСЛОС) генератора тестовой последовательности (ГТП) и анализатора тестовых реакций (АТР) степени 5. В этом случае полиномы РСЛОС ГТП и АТР одинаковой степени, причем оба полинома примитивные (а значит, неприводимые).
- Для порождающих полиномов РСЛОС ГТП степени 10 и АТР степени, кратной десяти. В этом случае полином РСЛОС ГТП примитивный, а полином АТР кратной степени, причем полиномы примитивные (а значит, неприводимые).
- Для порождающих минимальных полиномов РСЛОС ГТП степени 12 и АТР степени, кратной двенадцати. В этом случае полином РСЛОС ГТП примитивный, а полином АТР минимальный, причем полиномы неприводимые, но не всегда примитивные.
- Для порождающих полиномов РСЛОС ГТП и АТР, построенных на основе полиномов кодов циклического кодирования, в частности, кодов Хэмминга, Боуза-Чоудхури-Хоквингема, Рида-Соломона, Файра.
- Для рассмотренных вариантов компактного тестирования предложены рекомендации для наиболее оптимальных сочетаний порождающих полиномов.
Достоверность научных положений, выводов и практических рекомендаций подтверждена математическими доказательствами утверждений, сформулированных в работе, результатами компьютерного моделирования.
6. Планируемые практические результаты
Практическая ценность работы. На основе результатов, полученных в работе, удается выбрать комбинации генератора и сигнатурного анализатора в схеме встроенного тестирования ПЛИС, обеспечивающие 100% обнаружение одиночных неисправностей в блоке И; строить системы встроенного контроля для конкретных устройств, находить достоверность контроля, обеспечиваемой дополнительным оборудованием, в рамках выбранной модели неисправностей.
Теоретические результаты работы включены в специальные курсы для студентов, специализирующихся в области САПР цифровых схем: “Теория помехоустойчивого кодирования”, “Теория кодов, корректирующих ошибки”, “Системы контролепригодного проектирования КС”.
7. Апробация работы
Результаты работы докладывались на конференциях:
V Международная научно-техническая конференция студентов, аспирантов и молодых ученых, 22-23 апреля 2014, г.Донецк;
VI Международная научно-техническая конференция студентов, аспирантов и молодых ученых, 20-22 мая 2015, г.Донецк;
Компьютерная и программная инженерия. Международная научно-техническая конференция студентов, аспирантов и молодых учёных 15-16 декабря 2015 года. - Донецк.
8. Содержание работы
Основные результаты работы освещены в публикациях.
Альтернативные методы циклического кодирования и аппаратной реализации кодирующих и декодирующих устройств
Коды Рида-Соломона были предложены уже более полувека назад, однако они продолжают оставаться предметом внимания и исследования. Это связано, прежде всего, с появлением все новых областей их использования, теперь уже не только в задачах связи, но и в широком применении для задач цифровой техники.
В настоящее время имеет место тенденция реализации аппаратных проектов с применением языков описания аппаратуры (VHDL, Verilog), которые позволяют осуществить проектирование, верификацию цифровых схем на различных уровнях абстракции и реализацию (например, в виде СБИС) на основе технологии FPGA. Такой подход имеет ряд преимуществ. Например, он более гибок при изменении схемы или уровня технологии изготовления ИС, кроме того, он более дешевый по сравнению с применением заказных ИС (ASIC). Поэтому вопросы построения и аппаратной реализации кодов Рида-Соломона являются актуальными, учитывая все большую их популярность и востребованность для различных сфер применения.
Проведенный анализ литературы [2-8] отражает широчайший спектр разработанных и уже используемых на практике кодов Рида-Соломона. Можно привести несколько наиболее известных примеров: (255, 223, 33) код Рида-Соломона для космической связи NASA, укороченные коды Рида-Соломона над полем Галуа GF(256) для CD-ROM, DVD и цифрового телевидения высокого разрешения (формат HDTV), расширенный (128, 122, 7) код Рида-Соломона над полем Галуа GF(128) для кабельных модемов. Существует несколько коммерческих аппаратных реализаций - ряд интегральных схем (ИС), предназначенных для кодирования и декодирования кодов Рида-Соломона. При этом реализованные коды имеют разные корректирующие способности, и, как следствие, разный уровень сложности и сферы применения. Например, код Рида-Соломона (255, k), где k – количество информационных символов кода, для различных ИС может исправлять, как правило, от 1 до 16 ошибочных символов.
Кроме того, коды Рида-Соломона можно использовать не только для помехоустойчивого кодирования при передаче данных, а также везде, где есть необходимость в предотвращении искажения информации, например [6]:
- обнаружение и исправление ошибок в поврежденных или дефектных носителях информации;
- обнаружение и исправление ошибок при умышленном изменении информационных сообщений с целью дезинформации;
- обнаружение и исправление модификации информации об авторе или исполняемого кода с целью
взлома
программного обеспечения; - защита программного обеспечения или данных от копирования с лицензионного диска;
- восстановление одного или нескольких томов многотомного архива, искаженных или вообще потерянных при загрузке из сети;
- обнаружение и исправление ошибок в цепочках ДНК в генной инженерии.
Задача сравнительного анализа способов построения кодов Рида-Соломона, исправляющих двойные ошибки, появилась после публикации работы [8], в которой рассматриваются вопросы реализации кодера и декодера (255, 251) кода в FPGA. Вместе с тем, в работах [5-8] основное внимание уделяется другим принципам построения подобных кодов, отличающихся более простыми методами декодирования.
Прежде всего, следует отметить, что коды Рида-Соломона, исправляющие одиночные или двойные ошибки, независимо от того, по какому полю Галуа они построены, укорочены, посимвольно перемежены или нет, допускают применение метода синдромного декодирования. Такой метод неприменим для кодов исправляющих большое количество ошибок. Для них типичный декодер основан на блоках вычисления синдрома, буферного регистра, решения ключевого уравнения на основе одного из алгоритмов, например, Берлекэмпа-Месси, iBM, riBM, RiBM, алгоритма Евклида или Питерсона- Горенcтейна-Цирлера (в [8] - алгоритм iBM), поиска корней полиномов локаторов ошибок на основе алгоритма Ченя, расчета значения ошибки (алгоритм Форни), коррекции ошибок.
Рассмотрим некоторые варианты аппаратной реализации циклических кодов. Все они основаны на применении регистров сдвига с линейными обратными связями.
Аппаратная реализация кодов БЧХ
Порождающий полином кода БЧХ, исправляющего S ошибок, должен содержать 2S корней. Для вычисления этого полинома используют минимальные полиномы, полученные для некоторого поля Галуа. Размер поля Галуа выбирается в зависимости от необходимой длины и корректирующих возможностей кода. Если для построения кода выбрать поле Галуа GF(16), то длина неукороченного кода будет равна 15 для любой (до семи для этого поля) кратности исправляемых ошибок [5, 7, 10-12].
В качестве примера на рисунке 1 представлен декодер кода БЧХ (15, 7), исправляющего двойные ошибки.

Рисунок 1 - Декодер (15, 7) кода БЧХ, исправляющего двойные ошибки (Test for all 0’s or one 1 – проверка на наличие не более одного ненулевого бита)
Аппаратная реализация кодов БЧХ
Для код Рида – Соломона, исправляющего s ошибок является частным случаем кода БЧХ. В отличие от большинства распространенных циклических кодов, код Рида-Соломона является недвоичным, т.е. символом этого кода является не один двоичный разряд, а несколько.
Декодер кода Рида – Соломона аналогичен декодеру кода БЧХ (рис. 1).
Разница заключается в интерпретации элементов: памяти – триады (рис. 2, на рисунке 3 – пример реализации декодера перемеженного кода), тетрады (рис. 4), пентады, гексады, гептады, огдоады (рис.5), эннеады, декады; умножителей на константу и сумматоров.

Рисунок 2 - Декодер (7, 5) кода Рида-Соломона, исправляющего одиночные ошибочные триады (Test for all 0’s – проверка на все нули)
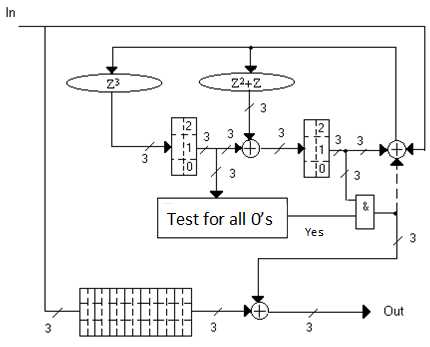
Рисунок 3 - Декодер для посимвольно перемеженного (7,5) кода Рида-Соломона с параметром перемежения j=2 (Test for all 0’s – проверка на все нули)

Рисунок 4 - Декодер (15, 11) кода Рида-Соломона, исправляющего двойные ошибочные тетрады (Test for at most one nonzero tetrad – проверка на наличие не более одной ненулевой тетрады)

Рисунок 5 - Декодер (255, 251) кода Рида-Соломона, исправляющего двойные ошибочные байты (Test for at most one nonzero byte – проверка на наличие не более одного ненулевого байта)
Для построения декодера на элементах двоичной логики необходимо умножители на константу представить в виде сумматоров по модулю два. Они строятся на основе приведения по модулю порождающего полинома соответствующего поля Галуа произведения коэффициента умножителя на константу и элемента поля в общем виде.
По полученному остатку от деления строится схема умножителя на константу. Остальные элементы кодера и декодера для аппаратной реализации (255, 251) кода Рида-Соломона на элементах двоичной логики не требуют каких-либо специальных расчетов или методов построения.
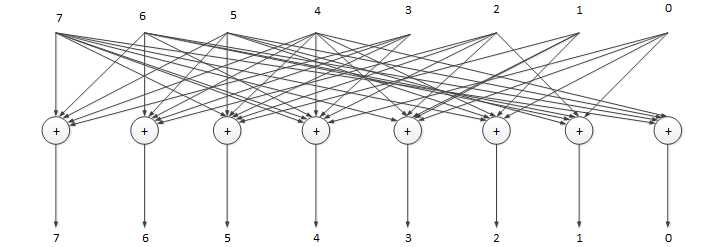
Рисунок 6 - Реализация умножителя на константу для псевдопеременной X3 на элементах двоичной логики
Основная задача рисунка 6 – дать общее представление реализации умножителя на сумматорах по модулю два.
Рассмотренные способы декодирования и преобразования умножителей могут быть применимы не только для данного кода, но также для любых кодов Рида-Соломона, исправляющих одиночные или двойные ошибки, посимвольно перемеженных и/или укороченных.
Рассмотренные варианты реализации кодов БЧХ и Рида-Соломона имеют простой способ декодирования (вылавливание ошибок), были проиллюстрированы общие черты и различия их декодеров. Поэтому в настоящее время они широко распространены как в аппаратной, так и в программной реализации. Кроме того, рассмотренные варианты можно использовать для метода посимвольного перемежения. Многие вопросы, связанные с построением кодов Рида-Соломона и с алгеброй полей Галуа, становятся более понятными при иллюстрации их конкретными примерами реализации.
Альтернативные методы компактного тестирования на основе методов циклического кодирования
Одним из способов повышения тестопригодности СБИС микропроцессоров, устройств на ПЛИС является применение встроенных средств контроля, реализующих методы компактного тестирования. Метод сквозного сдвигового регистра (LSSD - level sensitive scan design) - другой широко известный способ снижения трудоемкости тестирования дискретных устройств. Метод LSSD сводит задачу тестирования к проверке нескольких регистров сдвига и комбинационных схем. Наиболее совместимым с методом LSSD из широкого ряда методов компактного тестирования является сигнатурный анализ, поскольку основой анализатора тестовых реакций (АТР) в этом случае является регистр сдвига с линейными обратными связями (РСЛОС). С помощью незначительных аппаратных затрат сдвиговые регистры преобразуются в РСЛОС, которые выполняют роль генераторов тестовых последовательностей (ГТП) и АТР для тестирования комбинационных схем (КС). Реализация методов компактного тестирования ставит задачу определения достоверности результатов контроля. В работе [3] рассматриваются вопросы комплексной оценки достоверности тестирования КС при применении ГТП и АТР в виде РСЛОС, которая учитывает не только обнаруживающие способности АТР, но также структуру ГТП и характер тестовых реакций объекта диагностики. В частности, получен вывод о значительной зависимости эффективности сигнатурного анализа от выбора того или иного сочетания порождающих полиномов РСЛОС ГТП и АТР. Данная работа представляет собой продолжение исследований в этом направлении.
Полученные результаты могут быть реализованы на основе РСЛОС как в конфигурации Галуа (например, рис. 1-5), так и в конфигурации Фибоначчи [10]. Пример РСЛОС ГТП в конфигурации Фибоначчи представлен на рисунке 7.
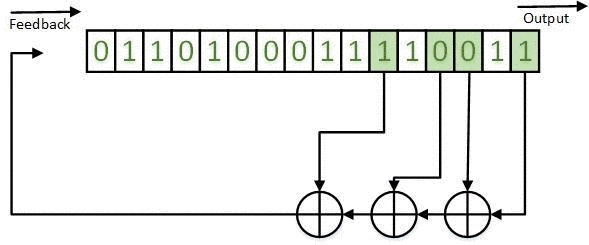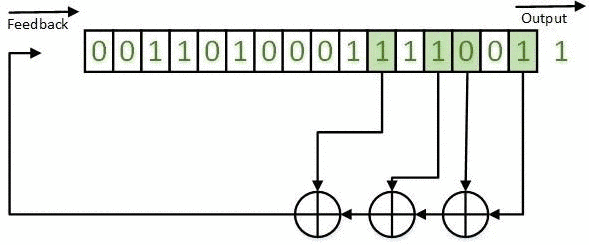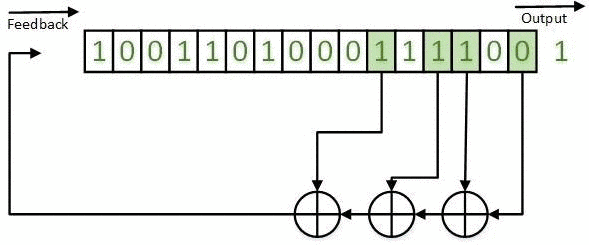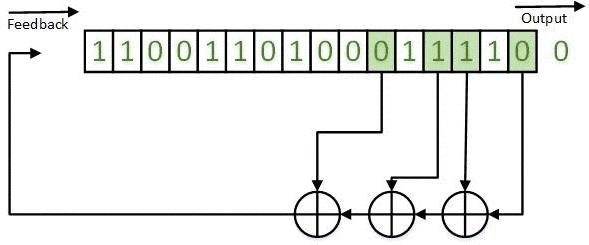
Рисунок 7 - РСЛОС ГТП в конфигурации Фибоначчи. Анимация состоит из 7 кадров с задержкой 1 с между кадрами; 7 повторов; 116 килобайт
Более детально с результатами работы можно ознакомиться в следующих публикациях [11-22].
Заключение
В работе предложены следующие альтернативные методы циклического кодирования и аппаратной реализации кодирующих и декодирующих устройств: варианты аппаратной реализации кодов БЧХ и Рида-Соломона, исправляющих одиночные и двойные ошибки (пакетов ошибок) и использующих синдромный метод декодирования; метод укорачивания и аппаратная реализация циклических кодов на основе двойственных полиномов; альтернативный метод деления полиномов; метод укорачивания и аппаратная реализация циклических кодов на основе альтернативного деления полиномов.
Выполнен анализ эффективности компактного тестирования на основе циклического кодирования с локализацией ошибок в выходной тестовой реакции проверяемой комбинационной схемы. Предложен метод аналитического расчета сигнатур для исчерпывающего тестирования комбинационных схем при реализации генератора тестовых последовательностей и анализатора тестовых реакций на основе регистров сдвига с линейными обратными связями. Рассматриваются анализаторы тестовых реакций, построенные на основе циклических кодов Хэмминга, Боуза-Чоудхури-Хоквингема, Бартона, Рида-Соломона, позволяющие локализовать ошибки в тестовой реакции. Получена оценка меры эффективности компактного тестирования комбинационных схем, на основе которой предложены рекомендации по выбору порождающих полиномов регистров сдвига с линейными обратными связями для различных вариантов компактного тестирования с локализацией ошибок. Полученные результаты могут найти применение для встроенного самотестирования или внешнего тестового оборудования средств вычислительной техники.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2018 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Белл Д. Грядущее постиндустриальное общество. Опыт социального прогнозирования: Пер. с англ. 2-е изд., испр. и доп. – М.: Academia, 2004. – 788 с.
- Гладких А. А. Методы эффективного декодирования избыточных кодов и их современные приложения / А. А. Гладких, Р. В. Климов, Н. Ю. Чилихин. – Ульяновск : УлГТУ, 2016. – 258 с.
- Улучшение радиационной стойкости памяти с помощью помехоустойчивых кодов / А.Н. Ершов [и др.] // Ракетно-космическое приборостроение и информационные системы. 2014, том 1, выпуск 4, c. 42–49.
- Ярмолик В.Н. Тестовое диагностирование аппаратного и программного обеспечения вычислительных систем / В.Н. Ярмолик, А.А. Иванюк // Доклады БГУИР, № 2 (80), 2014. – С.127–142.
- Richard E.Blahut. Algebraic Codes for Data Transmission/ Cambridge University Press, 2012. – 498 p.
- Рахман П.А. Основы защиты данных от разрушения. Коды Рида-Соломона/ Интернет-ресурс. – Режим доступа: https://bugtraq.ru...
- Питерсон У. Коды, исправляющие ошибки / У. Питерсон, Э. Уэлдон. – М.: Мир, 1976. – 595 с.: ил.
- Design of RS (255, 251) Encoder and Decoder in FPGA / Anindya Sundar Das, Satyajit Das and Jaydeb Bhaumik // International Journal of Soft Computing and Engineering (IJSCE) ISSN: 2231-2307, Volume-2, Issue-6, January 2013, pp. 391–394.
- Ярмолик В.Н. Эффективность сигнатурного анализа в самотестирующихся СБИС / В.Н. Ярмолик, Е.П. Калоша // Электрон. моделирование. 1992. 14, №3. С.51–56.
- Frohwerk R.A. Signature analysis, Hewlett-Packard J. 28, Nr. 9, 1977. – pp. 2–8.
- Дяченко В.О. Исследование способов проектирования кодов Рида-Соломона / В.О. Дяченко., Ю.Е. Зинченко, О.Н. Дяченко // Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС КМ-2014) : V Всеукраїнська науково-технічна конференція студентів, аспірантів та молодих вчених, 22-23 квітня 2014 р., м. Донецьк : зб. доп. / Донец. націонал. техн. ун-т; редкол. В.А.Світлична. – Донецьк: ДонНТУ, 2014. – в 2 тт. – т.2. – С. 72–78. – Режим доступа: http://ea.donntu.ru...
- Дяченко В.О. Анализ способов реализации кодов Рида-Соломона, исправляющих двойные ошибки / В.О. Дяченко, О.Н. Дяченко // Современные тенденции развития и перспективы внедрения инновационных технологий в машиностроении, образовании и экономике: материалы Международной научно-практической конференции (Азов, 19 мая 2014 г.). – Ростов н/Д, ДГТУ, 2014. – С. 18–22. – Режим доступа: http://ea.donntu.ru...
- Дяченко О.Н. Аппаратная реализация кодов БЧХ и кодов Рида-Соломона / О.Н. Дяченко, В.О. Дяченко // Современные тенденции развития и перспективы внедрения инновационных технологий в машиностроении, образовании и экономике: материалы IV Международной научно-практической конференции (Азов, 25 мая 2017 г.). – Ростов н/Д, ДГТУ, 2017. – С. 30–34. – Режим доступа: https://elibrary.ru...
- Дяченко В.О. Циклическое кодирование цифровой информации на основе двойственных полиномов / В.О. Дяченко, О.Н. Дяченко // Современные тенденции развития и перспективы внедрения инновационных технологий в машиностроении, образовании и экономике: материалы II Международной научно-практической конференции (Азов, 19 мая 2015 г.) [Электронный ресурс]. – Ростов н/Д, ДГТУ, 2015. – С. 71–76. – Режим доступа: http://ea.donntu.ru...
- Дяченко В.О. Особенности применения двойственных полиномов для аппаратной реализации циклических кодов / В.О. Дяченко, О.Н. Дяченко // Информационные управляющие системы и компьютерный мониторинг в рамках форума “Инновационные перспективы Донбасса” (ИУС КМ-2015): VI Международная научно-техническая конференция студентов, аспирантов и молодых ученых, 20-22 мая 2015, г.Донецк: / Донец. национал. техн. ун-т; сост.: К.Н.Маренич (председатель) и др. – Донецк: ДонНТУ, 2015. – С. 130–136. – Режим доступа: http://ea.donntu.ru...
- Дяченко О.Н. Альтернативный метод укорачивания циклических кодов / О.Н. Дяченко, В.О. Дяченко // Информатика, управляющие системы, математическое и компьютерное моделирование - 2016 в рамках в рамках II Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2016): VII Международная научно-техническая конференция студентов, аспирантов и молодых ученых, 26-27 мая 2016, г.Донецк: / Донец. национал. техн. ун-т; сост.: К.Н.Маренич (председатель) и др. – Донецк: ДонНТУ, 2016. – С. 328–334. – Режим доступа: http://ea.donntu.ru...
- Дяченко О.Н. Альтернативный метод укорачивания циклических кодов / О.Н. Дяченко, В.О. Дяченко // Электронные информационные системы. 2017. № 1 (12). С. 94–100. – Режим доступа: https://elibrary.ru/item.asp?id=28883888, http://ea.donntu.ru...
- Дяченко В.О. Альтернативный способ построения укороченных кодов Файра / В.О. Дяченко, О.Н. Дяченко // Компьютерная и программная инженерия. Сборник материалов международной научно-технической конференции студентов, аспирантов и молодых учёных 15-16 декабря 2015 года . - Донецк, ДонНТУ - 2015. – С. 86–89. – Режим доступа: http://ea.donntu.ru...
- Дяченко О.Н. Исследование эффективности компактного тестирования на основе методов циклического кодирования / О.Н. Дяченко, Ю.Е. Зинченко, В.О. Дяченко // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках III форума
Инновационные перспективы Донбасса
(ИУСМКМ - 2017): VIII Международная научно-техническая конференция, 26 мая 2017, г. Донецк: / Донец. национал. техн. ун-т; редкол. Ю.К. Орлов и др. – Донецк: ДонНТУ, 2017. – С. 313–319. – Режим доступа: http://iuskm.donntu.ru... - Дяченко О.Н. Применение методов помехоустойчивого кодирования для компактного тестирования цифровых схем / О.Н. Дяченко, Ю.Е. Зинченко, В.О. Дяченко // Информатика и кибернетика. Донецк: ДонНТУ, 2017. № 3(9). – С. 55–59. – Режим доступа: http://infcyb.donntu.ru...
- Дяченко В.О. Компактное тестирование на основе минимальных полиномов в цифровых схемах с самотестированием / В.О. Дяченко, О.Н. Дяченко // V Международная научно-техническая конференция “Современные информационные технологии в образовании и научных исследованиях” СИТОНИ – 2017, 20 ноября 2017 – Донецк: ДонНТУ, 2017. – Режим доступа: http://pm.conf.donntu.ru...
