Українська   Русский
DonNTU   Masters' portal

Contents

Introduction

Occurring in the last decades the dynamic changes in different spheres of society's activities are characterized by avalanche-like growth of very different kinds of information: social, political, industrial, scientific, cultural, etc. international experience shows that the information potential of society is becoming increasingly determine its economic potential together with the material production. Economic development of the society will be entirely determined by the results of intellectual activity. This is due to increasing role of information, which becomes crucial for the development of different spheres of society.       

1. Relevance and motivation

Recognized classic of the theory of post-industrialism, D. Bell identifies three technological revolutions: the invention of a steam engine in the 18th century; scientific and technological achievements in the field of electricity and chemistry in the XIX century; the creation of computers in the XX century [1].       

Modern civilization of the XXI century is experiencing another revolution - information. The rapid growth of the World Wide Web leads to the formation of a digital civilization: if in 2000 there were 359 million Internet users, then in March 2017 the number of users is already 3732 million - this is half the world's population. In the media, the coming zetta-byte era of human development is increasingly being announced. According to optimistic forecasts, in the period from 2012 to 2020, there will be a doubling of data every year and at the end of this period it will amount to approximately 37 zettabyte [2].       

             

Advantages of information and robotics can not be overestimated. In recent decades, advances in the introduction of information technology are one of the determining factors of the economic potential of society. As a result, the information infrastructure is emerging and developing, which provides new services, such as distance education, telework, telemedicine, e-commerce, ordering tickets for transport, Internet banking, paying bills, etc. At the same time, the increase in the amount of information that is transmitted , stored and processed, leads to the requirements of ensuring its reliability and reliability of the hardware and software used. From the successful solution of these tasks, on the one hand, depends the prosperity of the present civilization, or, on the other hand, its self-destruction, for example, because of accidental or deliberate failure in military applications. In addition, it is necessary to take into account such phenomena as solar activity and hard cosmic radiation.       

              

Reducing the topological design standards of the VLSI memory increases the IS sensitivity to local radiation effects. In this case, not only can the number of errors increase, but also their character can change. In this case, the task of increasing the fault tolerance of memory with the help of noise-immune codes becomes especially urgent [3].       

               

Therefore, to eliminate possible errors due to natural phenomena, or artificial causes, or defects of hardware information tools, to protect against destruction caused by hard cosmic radiation, modern technologies of noise-immune coding are used in the design of memory chips, the entire range of methods and means of embedded self-testing of digital systems [1–22].       

      

2. Goals and objectives

The aim of the work is to develop methods for cyclic coding, new methods for compact testing, to study their reliability, and to develop schemes that implement these methods.

         

The studies were conducted in the following directions.

               
  1. Development of alternative methods for cyclic coding, as well as hardware implementation of coding and decoding devices.
  2. Development of alternative methods for compact testing based on cyclic coding methods.
  3. Experimental verification of the theoretical results obtained with the help of CAD-tools Active-HDL.

3. Contents

Alternative methods of cyclic encoding and hardware implementation of coding and decoding devices.

Reed-Solomon codes have been proposed for more than half a century ago, but they continue to be the subject of attention and research. This is due, first of all, to the appearance of ever new areas of their use, now not only in communication tasks, but also in a wide application for digital technology tasks.

At present, there is a tendency to implement hardware projects using hardware description languages (VHDL, Verilog), which allow the design, verification of digital circuits at various levels of abstraction and implementation (for example, VLSI) based on FPGA technology. This approach has several advantages. For example, it is more flexible when changing the circuitry or the level of the IC manufacturing technology; in addition, it is cheaper compared to the use of ASICs. Therefore, the issues of the construction and hardware implementation of Reed-Solomon codes are relevant, given their increasing popularity and relevance for various applications.

The analysis of literature [2-8] reflects a wide range of Reed-Solomon codes developed and already in use. Here are some of the best-known examples: the Reed-Solomon code for NASA space communications, the shortened Reed-Solomon codes over the Galois field GF(256) for CD-ROMs, DVDs and high-definition digital television (HDTV format) (255, 223, 33), extended (128, 122, 7) Reed-Solomon code over the Galois field GF(128) for cable modems. There are several commercial hardware implementations - a number of integrated circuits (ICs) designed for encoding and decoding Reed-Solomon codes. At the same time, the implemented codes have different correcting abilities, and, as a consequence, a different level of complexity and scope of application. For example, the Reed-Solomon code (255, k), where k is amount of information code symbols, for various ICs can usually correct from 1 to 16 erroneous symbols.

In addition, Reed-Solomon codes can be used not only for noise-immune encoding in data transmission, but also wherever there is a need to prevent distortion of information, for example [6]:

The problem of a comparative analysis of the methods for constructing Reed-Solomon codes correcting double errors appeared after the publication of [4], which deals with the implementation of the encoder and decoder (255, 251) of the code in the FPGA. At the same time, in papers [5-8] the main attention is paid to other principles of constructing similar codes, which are distinguished by more simple methods of decoding.

First of all, it should be noted that Reed-Solomon codes that correct single or double error, regardless of which field the Galois they are built, shortened, symbol by symbol interleaved or not, to allow for the use of the method of syndrome decoding. This method is not applicable to codes correcting many errors. For them, a typical decoder based on the blocks calculate the syndrome, buffer register, the solution of the key equation based on one of algorithms, for example, Berlekamp-Massey, iBM, riBM, RiBM, the Euclidean algorithm or Peterson - Gorenstein - Zierler (in [4] algorithm iBM), seeking the roots of polynomials of the locator errors on the basis of Chen's algorithm, calculate the error value (Forney algorithm), error correction.

Consider some of the options for the hardware implementation of cyclic codes. They are all based on using shift registers with linear feedback.

Hardware implementation of BCH codes

The generator polynomial for BCH code correcting S errors must contain 2S roots. To calculate this polynomial, we use the minimal polynomials obtained for some Galois field. The size of the Galois field is selected depending on the required length and corrective capabilities of the code. If you select the Galois field GF(16) to construct the code, then the length of the no shortened code will be 15 for any (up to seven for this field) multiplicity of corrected errors [5, 7, 10-12].

As an example, Figure 1 shows decoder for BCH (15, 7) code that corrects double errors.

Decoder for BCH (15, 7) code correcting double errors

Figure 1 – Decoder for BCH (15, 7) code correcting double errors

Hardware implementation of Reed-Solomon codes

The Reed-Solomon code, correcting s errors, is a particular case of the BCH code. Unlike most common cyclic codes, the Reed-Solomon code is non-binary one, i.e. the symbol of this code is not single, but several binary digits.

The decoder of the Reed-Solomon code is similar to the decoder of the BCH code (Fig. 1).

The difference lies in the interpretation of the elements: the memory is a triads (Figure 2, in Figure 3 is an example of an implementation of the interleaved code decoder), tetrads (Figure 4), pentads, hexads, heptads, ogdoads (Fig. 5), enneads, decades; multipliers by a constant and adders.

Decoder for a (7, 5) Reed-Solomon code correcting single erroneous triads

Figure 2 - Decoder for a (7, 5) Reed-Solomon code correcting single erroneous triads

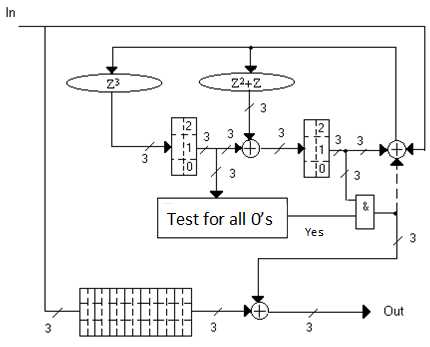
Decoder for the symbol-interleaved (7, 5) Reed-Solomon code with the interleaving parameter j = 2

Figure 3 - Decoder for the symbol-interleaved (7, 5) Reed-Solomon code with the interleaving parameter j = 2

Decoder for a (15, 11) Reed-Solomon code correcting double erroneous tetrads

Figure 4 - Decoder for a (15, 11) Reed-Solomon code correcting double erroneous tetrads

Decoder for a (255, 251) Reed-Solomon code correcting double erroneous bytes

Figure 5 - Decoder for a (255, 251) Reed-Solomon code correcting double erroneous bytes

To construct a decoder on binary logic elements, it is necessary to represent multipliers by a constant in the form of modulo-2 adders. They are constructed on the basis of reduction modulo the generating polynomial of the corresponding Galois field of the product of the multiplier coefficient by the constant and the field element in a general form.

The multiplier by a constant circuit is constructed, using the obtained remainder from division. The remaining elements of the encoder and decoder for the hardware implementation (255, 251) Reed-Solomon code on binary logic elements do not require any special calculations or construction methods.

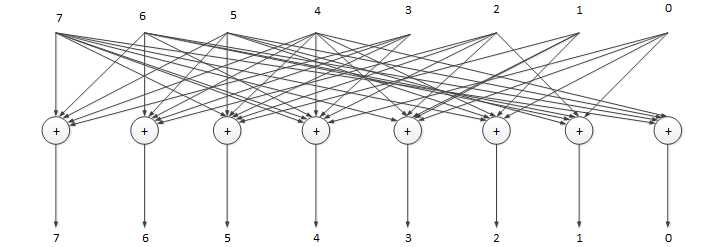
Implementation of multiplier by a constant for pseudo-variable X3 on binary logic elements

Figure 6 - Implementation of multiplier by a constant for pseudo-variable X3 on binary logic elements

The main task of Figure 6 is to give a general representation of the implementation of the multiplier on the modulo-2 adder.

The considered methods for decoding and converting multipliers can be applied not only for this code, but also for any Reed-Solomon codes correcting single or double errors, symbol-interleaved and / or shortened codes.

The considered variants of the BCH and Reed-Solomon codes have a simple method of decoding (trapping errors), common features and differences of their decoders were illustrated. Therefore, at present they are widely used both in hardware and in software implementation. In addition, the considered variants can be used for the method of symbol-by-symbol interleaving. Many questions connected with the construction of Reed-Solomon codes and with the algebra of Galois fields become clearer when illustrated by concrete examples of their implementation.

The considered variants of the BCH and Reed-Solomon codes have a simple method of decoding (trapping errors), common features and differences of their decoders were illustrated. Therefore, at present they are widely used both in hardware and in software implementation. In addition, the considered variants can be used for the method of symbol-by-symbol interleaving. Many questions connected with the construction of Reed-Solomon codes and with the algebra of Galois fields become clearer when illustrated by concrete examples of their implementation.

One way to increase the testability of the VLSI microprocessors, devices on FPGAs is the use of built-in monitoring tools that implement methods of compact testing. The LSSD method is another widely known method of reducing the complexity of testing discrete devices. The LSSD method reduces the testing task to checking several shift registers and combinational circuits. The most compatible with the LSSD method from a wide range of compact test methods is signature analysis, since the basis of the test response analyzer (TRA) in this case is the linear feedback shift register (LFSR). Using the low hardware costs, shift registers are converted into LFSR, which serve as test sequence generators (TSGs) and TRAs for testing combinational circuits (CC). The implementation of methods of compact testing raises the problem of determining the reliability of control results. In work [3] the questions of complex estimation of reliability of testing of CC at application of TSG and TRA in the form of LFSR are considered, which takes into account not only the detecting abilities of ATR, but also the structure of TSG and the nature of test responses of the diagnostic object. In particular, it was concluded that the effectiveness of signature analysis is highly dependent on the choice of a particular combination of the generating polynomials of the LFSR TSG and TRA. This work represents a continuation of research in this direction.

The obtained results can be realized on the basis of LFSR both in the Galois configuration (for example, in Figures 1-5) and in the Fibonacci configuration. An example of a LFSR TSG in the Fibonacci configuration is shown in Figure 7.

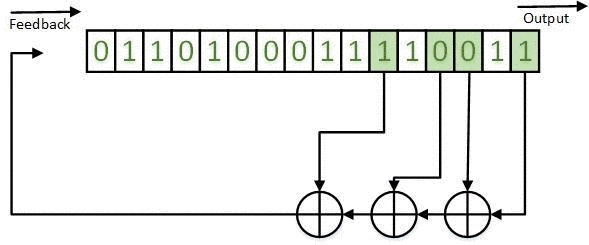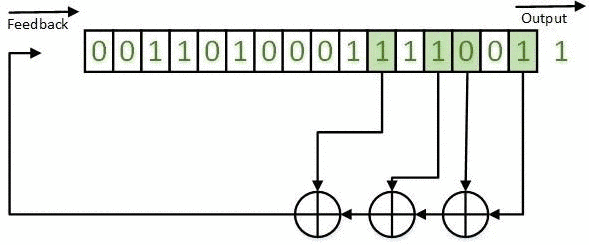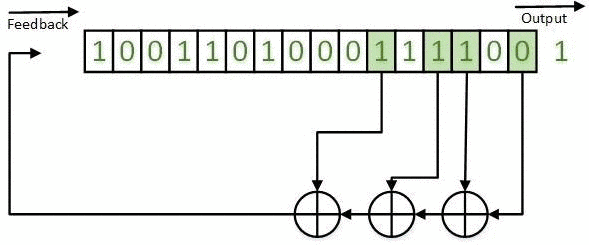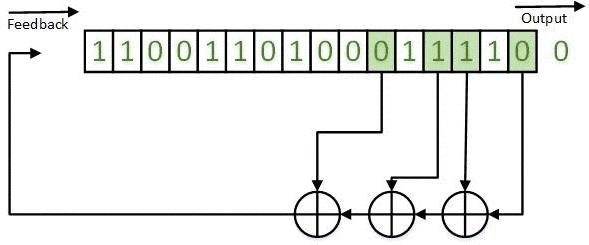
LFSR TSG in the Fibonacci configuration

Figure 7 - LFSR TSG in the Fibonacci configuration

Conclusion

The following alternative methods of cyclic encoding and hardware implementation of encoding and decoding devices are proposed: hardware versions of BCH and Reed-Solomon codes correcting single and double errors (error burst) and using the syndrome decoding method; method of shortening and hardware implementation of cyclic codes based on dual polynomials; an alternative method for division polynomials; method of shortening and hardware implementation of cyclic codes based on the alternative division of polynomials.

The effectiveness of compact testing on the basis of cyclic coding with localization of errors in the output test response of the tested combinational circuits is analyzed. A method of analytical calculation of signatures for exhaustive testing of combinational circuits is proposed for the implementation of a test sequence generator and a test response analyzer based on shift registers with linear feedbacks. Analyzers of test reactions are constructed based on the cyclic codes Hamming, Bose-Chaudhuri-Hocquenghem, Burton, Reed-Solomon, which allow localizing errors in the test response. The estimation of a measure of efficiency of compact testing of combinational circuits is obtained, on the basis of which recommendations are offered on the choice of generating polynomials of linear feedback shift registers for various versions of compact testing with localization of errors. The obtained results can find application for the built-in self-test or external test equipment of computers.

The master's work is not yet complete. Final completion: June 2018. The full text of the work and materials on the topic can be obtained from the author or his supervisor after the specified date.

References

  1. Белл Д. Грядущее постиндустриальное общество. Опыт социального прогнозирования: Пер. с англ. 2-е изд., испр. и доп. – М.: Academia, 2004. – 788 с.
  2. Гладких А. А. Методы эффективного декодирования избыточных кодов и их современные приложения / А. А. Гладких, Р. В. Климов, Н. Ю. Чилихин. – Ульяновск : УлГТУ, 2016. – 258 с.
  3. Улучшение радиационной стойкости памяти с помощью помехоустойчивых кодов / А.Н. Ершов [и др.] // Ракетно-космическое приборостроение и информационные системы. 2014, том 1, выпуск 4, c. 42–49.
  4. Ярмолик В.Н. Тестовое диагностирование аппаратного и программного обеспечения вычислительных систем / В.Н. Ярмолик, А.А. Иванюк // Доклады БГУИР, № 2 (80), 2014. – С.127–142.
  5. Richard E.Blahut. Algebraic Codes for Data Transmission/ Cambridge University Press, 2012. – 498 p.
  6. Рахман П.А. Основы защиты данных от разрушения. Коды Рида-Соломона/ Интернет-ресурс. – Режим доступа: https://bugtraq.ru...
  7. Питерсон У. Коды, исправляющие ошибки / У. Питерсон, Э. Уэлдон. – М.: Мир, 1976. – 595 с.: ил.
  8. Design of RS (255, 251) Encoder and Decoder in FPGA / Anindya Sundar Das, Satyajit Das and Jaydeb Bhaumik // International Journal of Soft Computing and Engineering (IJSCE) ISSN: 2231-2307, Volume-2, Issue-6, January 2013, pp. 391–394.
  9. Ярмолик В.Н. Эффективность сигнатурного анализа в самотестирующихся СБИС / В.Н. Ярмолик, Е.П. Калоша // Электрон. моделирование. 1992. 14, №3. С.51–56.
  10. Frohwerk R.A. Signature analysis, Hewlett-Packard J. 28, Nr. 9, 1977. – pp. 2–8.
  11. Дяченко В.О. Исследование способов проектирования кодов Рида-Соломона / В.О. Дяченко., Ю.Е. Зинченко, О.Н. Дяченко // Інформаційні управляючі системи та комп’ютерний моніторинг (ІУС КМ-2014) : V Всеукраїнська науково-технічна конференція студентів, аспірантів та молодих вчених, 22-23 квітня 2014 р., м. Донецьк : зб. доп. / Донец. націонал. техн. ун-т; редкол. В.А.Світлична. – Донецьк: ДонНТУ, 2014. – в 2 тт. – т.2. – С. 72–78. – Режим доступа: http://ea.donntu.ru...
  12. Дяченко В.О. Анализ способов реализации кодов Рида-Соломона, исправляющих двойные ошибки / В.О. Дяченко, О.Н. Дяченко // Современные тенденции развития и перспективы внедрения инновационных технологий в машиностроении, образовании и экономике: материалы Международной научно-практической конференции (Азов, 19 мая 2014 г.). – Ростов н/Д, ДГТУ, 2014. – С. 18–22. – Режим доступа: http://ea.donntu.ru...
  13. Дяченко О.Н. Аппаратная реализация кодов БЧХ и кодов Рида-Соломона / О.Н. Дяченко, В.О. Дяченко // Современные тенденции развития и перспективы внедрения инновационных технологий в машиностроении, образовании и экономике: материалы IV Международной научно-практической конференции (Азов, 25 мая 2017 г.). – Ростов н/Д, ДГТУ, 2017. – С. 30–34. – Режим доступа: https://elibrary.ru...
  14. Дяченко В.О. Циклическое кодирование цифровой информации на основе двойственных полиномов / В.О. Дяченко, О.Н. Дяченко // Современные тенденции развития и перспективы внедрения инновационных технологий в машиностроении, образовании и экономике: материалы II Международной научно-практической конференции (Азов, 19 мая 2015 г.) [Электронный ресурс]. – Ростов н/Д, ДГТУ, 2015. – С. 71–76. – Режим доступа: http://ea.donntu.ru...
  15. Дяченко В.О. Особенности применения двойственных полиномов для аппаратной реализации циклических кодов / В.О. Дяченко, О.Н. Дяченко // Информационные управляющие системы и компьютерный мониторинг в рамках форума “Инновационные перспективы Донбасса” (ИУС КМ-2015): VI Международная научно-техническая конференция студентов, аспирантов и молодых ученых, 20-22 мая 2015, г.Донецк: / Донец. национал. техн. ун-т; сост.: К.Н.Маренич (председатель) и др. – Донецк: ДонНТУ, 2015. – С. 130–136. – Режим доступа: http://ea.donntu.ru...
  16. Дяченко О.Н. Альтернативный метод укорачивания циклических кодов / О.Н. Дяченко, В.О. Дяченко // Информатика, управляющие системы, математическое и компьютерное моделирование - 2016 в рамках в рамках II Международного Научного форума Донецкой Народной Республики (ИУСМКМ-2016): VII Международная научно-техническая конференция студентов, аспирантов и молодых ученых, 26-27 мая 2016, г.Донецк: / Донец. национал. техн. ун-т; сост.: К.Н.Маренич (председатель) и др. – Донецк: ДонНТУ, 2016. – С. 328–334. – Режим доступа: http://ea.donntu.ru...
  17. Дяченко О.Н. Альтернативный метод укорачивания циклических кодов / О.Н. Дяченко, В.О. Дяченко // Электронные информационные системы. 2017. № 1 (12). С. 94–100. – Режим доступа: https://elibrary.ru/item.asp?id=28883888,  http://ea.donntu.ru...
  18. Дяченко В.О. Альтернативный способ построения укороченных кодов Файра / В.О. Дяченко, О.Н. Дяченко // Компьютерная и программная инженерия. Сборник материалов международной научно-технической конференции студентов, аспирантов и молодых учёных 15-16 декабря 2015 года . - Донецк, ДонНТУ - 2015. – С. 86–89. – Режим доступа: http://ea.donntu.ru...
  19. Дяченко О.Н. Исследование эффективности компактного тестирования на основе методов циклического кодирования / О.Н. Дяченко, Ю.Е. Зинченко, В.О. Дяченко // Информатика, управляющие системы, математическое и компьютерное моделирование в рамках III форума Инновационные перспективы Донбасса (ИУСМКМ - 2017): VIII Международная научно-техническая конференция, 26 мая 2017, г. Донецк: / Донец. национал. техн. ун-т; редкол. Ю.К. Орлов и др. – Донецк: ДонНТУ, 2017. – С. 313–319. – Режим доступа: http://iuskm.donntu.ru...
  20. Дяченко О.Н. Применение методов помехоустойчивого кодирования для компактного тестирования цифровых схем / О.Н. Дяченко, Ю.Е. Зинченко, В.О. Дяченко // Информатика и кибернетика. Донецк: ДонНТУ, 2017. № 3(9). – С. 55–59. – Режим доступа: http://infcyb.donntu.ru...
  21. Дяченко В.О. Компактное тестирование на основе минимальных полиномов в цифровых схемах с самотестированием / В.О. Дяченко, О.Н. Дяченко // V Международная научно-техническая конференция “Современные информационные технологии в образовании и научных исследованиях” СИТОНИ – 2017, 20 ноября 2017 – Донецк: ДонНТУ, 2017. – Режим доступа: http://pm.conf.donntu.ru...