Содержание
- Введение
- 1. Модальное управление
- 2. Фильтр Баттерворта
- 3. Исследование системы позиционирования в среде Matlab
- Выводы
- Список источников
Введение
В последние годы в промышленности набирают стремительное развитие системы позиционного электропривода.
В следствие чего, свое место в электроприводе нашел саморегулируемый синхронный двигатель, также известный как сервопривод
.
В большинстве случаев, он представляет собой малоинерционный саморегулируемый двигатель с постоянными магнитами.
В сравнении с шаговым двигателем при тех же размерах и условиях, серводвигатель имеет более высокий крутящий момент и более высокую эффективность.
В системах позиционирования задание скорости определяется посредством разницы между текущим положением и ошибкой позиционирования. Одним из самых эффективных методов придать системе позиционирования инвариантные свойства и обеспечить предельное быстродействие и точность в динамических режимах – включить в ее состав модальный регулятор.
Модальное управление на данный момент является одним из наиболее перспективных методов синтеза управляющих устройств, используемых в системах автоматизации. Оно предоставляет разработчику широкие возможности при обеспечении требуемых показателей качества протекания процессов: устранение колебательности при наличии упругости и люфтов в кинематических связях, повышение быстродействия. В связи с этим вопросы анализа и синтеза систем модального управления электроприводами в последнее время, становятся все более актуальными и им уделяется большое внимание [5].
1. Модальное управление
Идея модального управления заключается в организации обратных связей по всем координатам системы, таким образом, чтобы характеристический полином имел желаемые свойства, такие как время переходного процесса и перерегулирование. Также система модального регулирования может обеспечивать заданную жесткость механической характеристики.
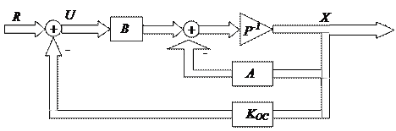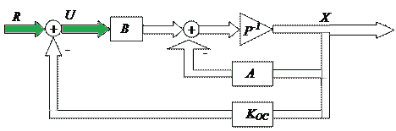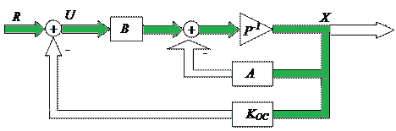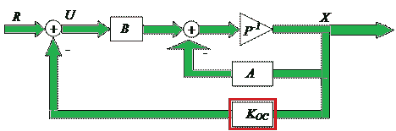
Рисунок 1 – Принцип модального регулирования
Анимация: 5 кадров, неограниченное количество повторений (размер 28.2 кБ)
В систему нужно ввести новый вектор входных сигналов U – вектор управляющих воздействий, связь которого со старым входным вектором R обеспечивается уравнением U=R-KосX. В таком случае наша система дифференциальных уравнений, которая описывает динамику нашей системы примет следующий вид:
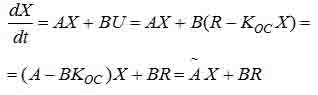
Как известно, динамику переходных процессов определяют корни характеристического полинома таким образом, определяя желаемый характер переходного процесса заданного полинома, возможно достигнуть необходимых для нас показателей качества.
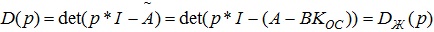
где Dж(p) – желаемый характеристический полином, определенный исходя из заданных показателей качества регулирования по методике косвенной корневой оценки.
Таким образом далее, решая эту систему уравнений относительно неизвестных нам коэффициентов Koc можно определить необходимые для нас коэффициенты отрицательной обратной связи по вектору состояния Х, которые и будут представлять из себя модальный регулятор. Но нельзя рассчитывать на то что мы можем таким образом реализовать любой переходной процесс для любой системы просто подставив в качестве желаемых любые корни, так как в процессе создания регулятора предполагается что система линейна, что в действительности не так, и таким образом мы можем синтезировать регулятор только для этой линейной части системы [1].
2. Фильтр Баттерворта
Наиболее важным этапом синтеза регулятора является корректный выбор желаемой передаточной функции, а именно ее вид и порядок, который можно определить из заданных требований к качеству регулируемого процесса.
Стандартные нормированные передаточные функции обычно имеют вид.
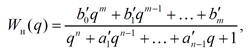
Желаемая передаточная функция приводится к виду
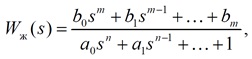
Ее коэффициенты при этом связаны с коэффициентами нормированной передаточной функции следующими формулами (3):
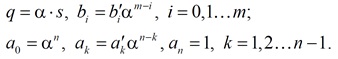
Коэффициент α=tp/τp поэтому требуемое время регулирования будет обеспечено при вычислении коэффициентов по формулам (3).
При выборе характеристического полинома рассматривались передаточные функции (ПФ) с одинаковыми полюсами, которые записаны на основании полиномов Ньютона, а также ПФ с полиномами Баттерворта. Наиболее часто в качестве желаемого принимают фильтр Баттерворта. Эти все функции не имеют нулей, а их числители являются константами, за счет чего можно обеспечить простоту реализации синтезируемого регулятора.
Передаточные функции с одинаковыми полюсами обладают монотонными переходными характеристиками. Если уменьшить время регулирования, это вызовет увеличение перерегулирования в системе. Как пример на рисунке 2 представлены переходные характеристики для ПФ с одинаковыми полюсами для полинома второго порядка. При повышении порядка характеристического полинома затягивается длительность переходного процесса. Для дальнейшего исследования выбраны характеристические полиномы второго порядка с временем регулирования 0,02 и 0,025 с.
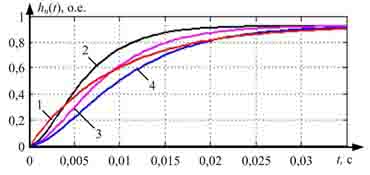
Рисунок 2 – Переходные характеристики для ПФ с одинаковыми полюсами (кривая 1 – характеристика исследуемой системы; кривая 2 – при tp=0.015 с; 3 – tp=0.02 с; 4 – tp=0.025 с)
Полиномы Баттерворта обычно записываются в виде соотношений с вещественными коэффициентами и нормируются по частоте среза ωc=1. Для выбора желаемой передаточной функции рассматривались характеристические полиномы второго и третьего порядков. Частота среза выбиралась по ЛАЧХ исследуемой системы и варьировалась от 100 до 300 рад/с [4]. Требования к распределению полюсов для второго и третьего порядков совпадают с распределением полюсов, которые получаются при оптимизации систем подчиненного регулирования второго и третьего порядков. Чем больше среднегеометрический корень, тем более быстродействующим будет фильтр, а, следовательно, и система, которую мы проектируем. Для второго порядка перерегулирование будет составлять G = 4,3%, для третьего G = 7,6%. Проведя анализ переходных характеристик, которые представлены на рисунке 3, можем видеть, что с ростом частоты среза уменьшается время переходного процесса, но вместе с тем растет величина перерегулирования и колебательность.
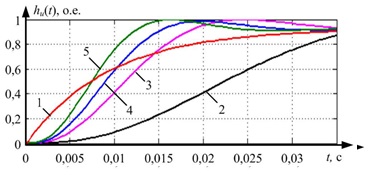
Рисунок 3 – Переходные характеристики для фильтра Баттерворта третьего порядка (кривая 1 – характеристика исследуемой системы; кривая 2 – при ωc=100; 3 – ωc=200; 4 – ωc=250; 5 – ωc=300)
На рисунке 4 изображены графики переходных характеристик при частоте среза, равной 250 рад/с для фильтров второго (n=2) и третьего (n=3) порядка. Из представленных графиков можно увидеть, что увеличение порядка фильтра увеличивает перерегулирование и повышает колебательность системы. Также это приводит к увеличению длительности переходного процесса.
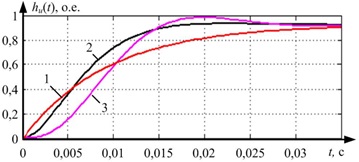
Рисунок 4 – Переходные характеристики для фильтра Баттерворта при ωc=250 (кривая 1 – характеристика исследуемой системы; кривая 2 – n=2; 3 – n=3)
Проведенные исследования показывают, что для данной задачи подходит именно система с применением фильтра второго или третьего порядка. Порядок фильтра принимаем равным степени характеристического полинома неизменяемой части исследуемой системы (n=2), а передаточная функция, рассчитанная при частоте среза, равной 250 рад/с, выбрана в качестве желаемой. Также можно использовать при построении регуляторов передаточные функции, построенные на полиномах Ньютона при tp=0.02 и 0.025 с.
По вышеизложенной методике для выбранных передаточных функций синтезировано несколько регуляторов, в основе которых лежат полиномы Баттерворта и полиномы Ньютона. Работа полученных регуляторов проверялась на имитационной модели системы позиционирования в среде Matlab [4].
3. Исследование системы позиционирования в среде Matlab
Среда Matlab позволяет, используя передаточные функции и визуальные блоки элементов, программно и аппаратно реализовать структурную схему электромеханической системы позиционирования.
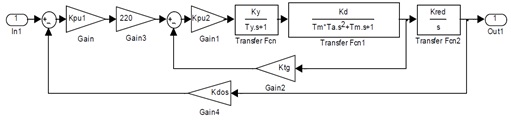
Рисунок 5 – Структурная схема двухконтурной электромеханической системы позиционирования
Структурная схема двухконтурной электромеханической системы управления состоит из системы автоматического регулирования скорости (САР) и системы позиционирования (СП) – рис.5.
СП предварительно настраивается по условиям эксплуатации с П-регулятором. САР скорости предусматривает, что при подаче на вход системы Uн = 220 В двигатель разгоняется до номинальной скорости nном. Изменяется Кпу2. Из условий работы переходная характеристика СП может быть апериодической 2-го порядка. Изменяется Кпу1.
На рисунке 6 показаны переходные характеристики системы позиционирования при изменении Кпу1.
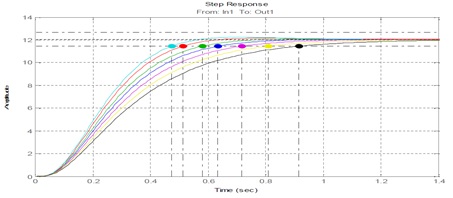
Рисунок 6 – Переходные характеристики СП при изменении Кпу1
Переходная характеристика СП с перерегулированием не более 0.05% при заданном допустимом отклонении Δ = ± 0.05 * hуст имеет наименьшее время регулирования.
Особенностью СП является то, что различные углы задания ее переходная характеристика отрабатывает с одним и тем же временем регулирования. Это можем видеть на рисунке 7.
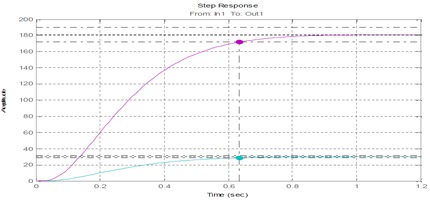
Рисунок 7 – Переходная характеристика СП при отработке различных углов задания
Сохранить форму переходной характеристики СП и уменьшить время регулирования при использовании П-регулятора невозможно, так как существует зависимость времени регулирования и перерегулирования от значения коэффициента регулятора Кпу1. Для уменьшения времени регулирования СП необходимо использовать модальный регулятор (МР).
В среде Matlab синтез заданных показателей качества регулирования с использованием МР требует векторно-матричного уравнения или уравнения пространства состояний СП.
При задании структурных схем в области Simulink одной из особенностей исследования систем автоматического управления является то, что в рабочей области Matlab при исследовании системы матрицы A, B, C и D не соответствуют матрицам исходной системы.
Матрица строка коэффициентов МР СП записывается: К = [К1 К2 К3 К4]. Уравнение СП с МР представляется
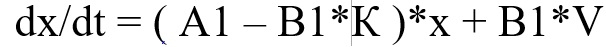
где V – скалярный вход, как сумма входного сигнала и выходного сигнала МР. В то время как динамические свойства исходной СП определяются матрицей А1, динамические свойства СП с МР определяются матрицей А = А1-В1*К.
При проектировании СП с МР первой особенностью является изменение амплитуды всех составляющих вектора состояний. Это значит, что при повышении быстродействия амплитуды составляющих вектора состояний превышают допустимые значения таких величин, как скорость, ток и напряжение двигателя.
Чувствительность переходной характеристики к изменению коэффициентов К1, К2, К3 и К4 является второй особенностью использования МР.
Оценим изменение коэффициентов К1, К2, К3 (коэффициент К4 не влияет) на относительное изменение перерегулирования σ/σо и относительное изменение времени регулирования tпу1/tpo.
При этом tpo = 0.182 с. – время регулирования переходного процесса в исходной структурной схеме СП с МР, а tp – время регулирования переходного процесса в структурной схеме СП с измененными значениями параметров МР. Перерегулирование переходного процесса в исходной структурной схеме с МР – σo = 0.05%, а σ – перегулирование переходного процесса в структурной схеме с доступом к переменным состояний с измененными значениями параметров МР.
Из приведенных выше результатов исследований можно сделать следующие выводы:
- Влияние произвольной вариации параметров МР на время регулирования в зависимости от К1, К2 и К3 имеет различную функциональную зависимость и степень влияния.
- Влияние произвольной вариации параметров МР на перерегулирование для коэффициентов К1, К3 имеет прямо пропорциональную функциональную зависимость, а для коэффициента К2 обратно пропорциональную функциональную зависимость.
- Произвольное изменение коэффициентов МР при сохранении формы переходной характеристики невозможно.
На рисунке 8 изображена схема исследования СП с МР и наблюдателем. Наблюдатель восстанавливает недостающие для реализации обратных связей (ОС) переменные Х3 и Х4.
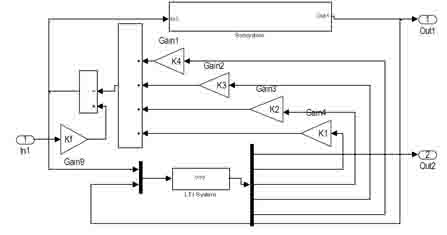
Рисунок 8 – Схема исследования СП с МР и наблюдателем
Коэффициент Kf введен для компенсации изменения амплитуды входного сигнала. Время регулирования переходной характеристики исходной СП tp = 0.582 с.
Применение МР, при заданном перегулировании σ = (0.04-0.05)%, соответствует повышению быстродействия в 3 раза.
Выводы по результатам сравнения МР с классическими регуляторами:
- Время регулирования и перерегулирование в СП с МР не изменяется.
- Переходная характеристика в СП с МР остается апериодической 2-го порядка.
- Время регулирования в СП с корректирующим устройством (КУ) изменяется не значительно, а перерегулирование увеличивается в десятки раз.
- Переходная характеристика в СП с КУ становится колебательной.
- Повышение быстродействия в СП с КУ ограничено зависимостью времени регулирования от перерегулирования.
Таким образом, исследования СП с МР доказали преимущество МР перед классическими способами проектирования [2].
Выводы
Проведенные исследования показали, что для синтеза регулятора по методу желаемой передаточной функции в качестве характеристического полинома целесообразно выбирать характеристические полиномы Ньютона второго порядка с временем регулирования 0.02 и 0.025 с, а также полином Баттерворта при частоте среза 250 рад/с.
Из результатов проведенных исследований можно сделать вывод, что применение модального регулятора обеспечивает наибольшее быстродействия системы позиционирования и заданных показателей качества управления. В отличие от классических регуляторов, модальный регулятор не вносит дополнительную инерционность в систему позиционирования.
В различных источниках, где описывается модальный регулятор, отмечаются некоторые недостатки, которые ограничивают его практическое применение. Поиск вариантов устранения этих недостатков и есть цель представленных и последующих исследований систем с модальным регулятором.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2019 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Модальное управление [Электронный ресурс]. – Режим доступа: studopedia.ru свободный.
- Анучин А. С. Системы управления электроприводов: учебник для вузов – М.: Издательский дом МЭИ, 2015. – 290 с.
- Харченко А. П., Слепокуров Ю. С., Аверьянов П. А. Исследование следящей системы в среде MATLAB // Вестник Воронежского государственного технического университета. – Воронеж:
ВГТУ
, 2017, №4 (том 13). – С. 7-11. - Рулевский В. М., Букреев В. Г., Шандарова Е. Б. Синтез субоптимального регулятора напряжения в системе электропитания глубоководного аппарата // Электротехнические системы и комплексы 2018. №3(40). – С. 47-54.
- Кочнева Т. Н., Кожевников А. В., Кочнев Н. В. Синтез модального регулятора и оценка эффективности модального управления для двухмассовых электромеханических систем // Вестник Череповецкого государственного университета 2013. №4 (Т.2). – С. 15-22.
- Фильтр Баттерворта [Электронный ресурс]. – Режим доступа: wikipedia.org свободный.
- Модальное управление [Электронный ресурс]. – Режим доступа: studfiles.net свободный.
