Разработка системы управления роботом манипулятором
Автор: А.А. Мымриков, П.И. Розкаряка
Источник: II Международная научно-практическая конференция Инновационные перспективы Донбасса
, ДонНТУ, 2016 г. – с. 220–226.
Аннотация
Одной из составляющих качественной подготовки современного специалиста является получение студентом навыков работы на всех стадиях создания новых устройств: от разработки – до монтажа и наладки.
Целью работы является создание прототипа робота-манипулятора для исследования и отладки алгоритмов позиционирования рабочего органа манипулятора с использованием современных прикладных программ.
На рис. 1 представлена обобщенная структура робота- манипуля- тора.
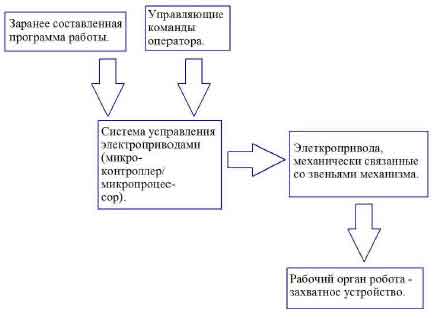
Рисунок 1 – Общая структура робота манипулятора
При разработке робота - манипулятора необходимыми являются требования:
- надежность в эксплуатации;
- гибкость программной логики;
- возможность производить изменения в управляющей программе без привлечения программистов.
Первым шагом было создание трехмерной модели робота в САПР (см. рис. 2).
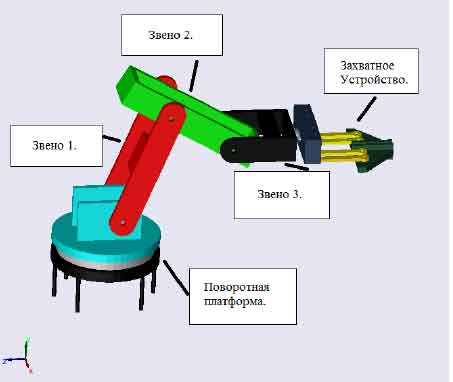
Рисунок 2 – Трехмерная модель робота, созданная в САПР Компас-3Д
Одним из важнейших этапов при разработке робота- манипулятора является решение кинематической задачи.
Различают прямую и обратную задачи кинематики.
Прямая задача кинематики заключается в нахождении координат рабочего органа по известным углам между звеньями.
Обратная задача кинематики заключается в нахождении углов между звеньями по заданным координатам рабочего органа манипу- лятора.
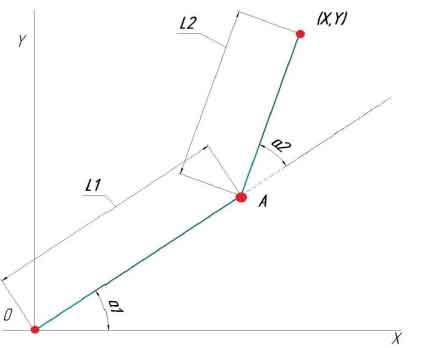
Рисунок 3 – Кинематическая схема робота - манипулятора в двухмерной плоскости
Пример решения прямой задачи:
Первое звено L1 манипулятора закреплено на поворотной плат- форме и повернуто на угол a1 относительно горизонтальной плоско- сти. Второе звено L2 закреплено на конце первого звена и повернуто относительно него на угол a2. Третье звено и захват в данной схеме не рассматриваются.
Решение прямой задачи сводится к нахождению координат X,Y по заданным L1, L2, a1 и a2. L1 и L2 – это длины звеньев 1 и 2, они определены физическими параметрами разрабатываемого манипуля- тора.
Имеется две системы отсчета – первая, связанная с точкой креп- ления звена 1–0, а вторая с началом координат в точке крепления зве- на 2–A.
Нахождение смещения второй системы относительно первой:
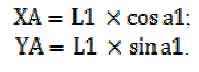
Координаты (X,Y) в системе отсчета второго звена:
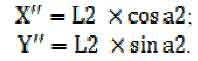
На рис. 3 видно, что в системе О второе звено повернуто относительно первого на a1+a2:
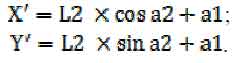
Таким образом, имеем:
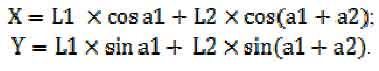
Пример решения обратной задачи:
Для решения обратной задачи дополним кинематическую схему манипулятора (см. рис. 4).
Обратная задача подразумевает нахождение таких углов a1 и a2, при которых манипулятор со звеньями L1 и L2 поместит рабочий ор- ган (в данной схеме крайнюю точку звена 2) в заданную точку (X,Y).
Проведем прямую В, соединяющую начало координат 0 с задан- ной точкой (X,Y).
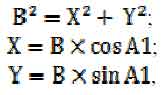
где A1 – угол между осью ОХ и прямой В; А2 – угол между прямой В и звеном L1. Откуда:
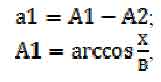
а угол A2 находим, воспользовавшись теоремой косинусов:
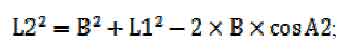
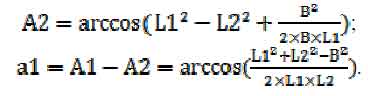
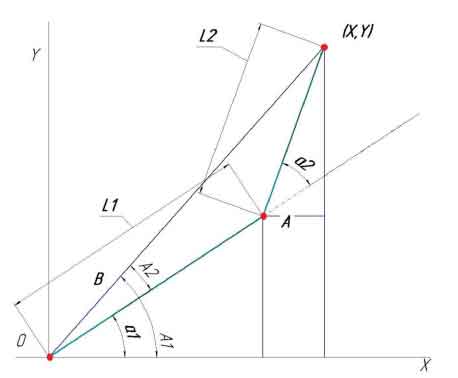
Рисунок 4 – Дополненная кинематическая схема
Угол для третьего звена будет рассчитываться исходя из требования, чтобы захват манипулятора был параллелен основанию.
Была осуществлена проверка результатов расчета кинематики моделированием в среде MATLAB Simulink, показавшая отсутствие ошибок при расчете углов.
Полученные значения углов служат заданием для каждого из электроприводов. Расчеты должен выполнять микроконтроллер. Для перемещений рабочего органа по заданным координатам необходимо применять позиционные электропривода. Основные требования, предъявляемые к электроприводу:
- точность поддержания заданного положения;
- скорость отработки заданного положения;
- надежность;
- малая масса привода.
Были выбраны следующие привода:
- привод звена 1 – TowerPro MG996R – электропривод с замкну- той по положению выходного вала системой управления. Металличе- ский редуктор с крутящим моментом 11 кг-см. Масса устройства – 55 гр.
- привод звеньев 2 и 3 – TowerPro SG5010 – электропривод с за- мкнутой по положению выходного вала системой управления. Крутя- щий момент – 6.5 кг-см. Масса устройства – 47 гр.
- привод захватного устройства Tower Pro 9g SG90. Электропри- вод, с системой управления замкнутой по положению выходного вала. Крутящий момент 1.6 кг-см. Масса устройства – 9гр.
- привод поворотной платформы – шаговый двигатель 28BYJ-48. Для реализации системы управления был выбран широко распро- страненный и доступный микроконтроллер фирмы Atmel – Atmega328p, имеющий необходимые аппаратные ресурсы для выполне- ния поставленной задачи.
Для связи контроллера с ПК используется интерфейсный преоб- разователь USB-UART TTL, реализованный на микроконтроллере Atmega16U2.
Программирование основного контроллера выполнялось на языке C в среде разработки AVR Studio 5.1, бесплатно распространяемой фирмой Atmel. Программное обеспечение для управления манипуля- тором с ПК разработано в среде Processing. Данная программа позво- ляет мышью указывать координаты в двухмерной плоскости XY и указывать угол поворота платформы относительно своей оси (рис.5).
Выводы
Созданный прототип робота манипулятора позволяет исследовать и про- изводить апробацию алгоритмов управления для решения задач кинематики при позиционировании рабочего органа манипулятора. Использование библиотеки Sim Mechanics позволило визуализировать переходные процессы.
Управление устройством может осуществляться как из среды MATLAB Simulink, так и из отдельной программы, разработанной в среде Processing. Про- грамма позволяет задавать желаемые координаты захвата манипулятора и переда- вать их непосредственно в контроллер манипулятора для выполнения.
Перечень ссылок
1. Мусалимов В.М., Г.Б. Заморуев, И.И. Калапышина, А.Д. Перечесова, К.А. Нуждин. Моделирование мехатронных систем в среде MATLAB (Simulink / SimMechanics): учебное пособие для высших учебных заведений. – СПб: НИУ ИТМО, 2013. – 114 с.