Abstract
We present a novel solution to the problem of recovering and tracking the 3D position, orientation and full articulation of a human hand from markerless visual observations obtained by a Kinect sensor. We treat this as an optimization problem, seeking for the hand model parameters that minimize the discrepancy between the appearance and 3D structure of hypothesized instances of a hand model and actual hand observations. This optimization problem is effectively solved using a variant of Particle Swarm Optimization (PSO). The proposed method does not require special markers and/or a complex image acquisition setup. Being model based, it provides continuous solutions to the problem of tracking hand articulations. Extensive experiments with a prototype GPU-based implementation of the proposed method demonstrate that accurate and robust 3D tracking of hand articulations can be achieved in near real-time (15Hz).
1 Introduction
The 3D tracking of articulated objects is a theoretically interesting and challenging problem. One of its instances, the 3D tracking of human hands has a number of diverse applications [6, 14] including but not limited to human activity recognition, human-computer interaction, understanding human grasping, robot learning by demonstration, etc. Towards developing an effective and efficient solution, one has to struggle with a number of complicating and interacting factors such as the high dimensionality of the problem, the chromatically uniform appearance of a hand and the severe self-occlusions that occur while a hand is in action. To ease some of these problems, some very successful methods employ specialized hardware for motion capture [21] or the use of visual markers as in [25]. Unfortunately, such methods require a complex and costly hardware setup, interfere with the observed scene, or both.
Several attempts have been made to address the problem by considering markerless visual data, only. Existing approaches can be categorized into model- and appearance-based. Model-based approaches provide a continuum of solutions but are computationally costly and depend on the availability of a wealth of visual information, typically provided by a multicamera system. Appearance-based methods are associated with much less computational cost and hardware complexity but they recognize a discrete number of hand poses that correspond typically to the method’s training set.

Figure 1: Graphical illustration of the proposed method. A Kinect RGB image (a) and the corresponding depth map (b). The hand is segmented (c) by jointly considering skin color and depth. The proposed method fits the employed hand model (d) to this observation recovering the hand articulation (e).
In this paper, we propose a novel model-based approach to the problem of 3D tracking of hand articulations which is formulated as an optimization problem that minimizes the discrepancy between the 3D structure and appearance of hypothesized 3D hand model instances, and its actual visual observations. Observations come from an off-the-shelf Kinect sensor [13]. Optimization is performed with a variant of an existing stochastic optimization method (Particle Swarm Optimization - PSO). The most computationally demanding parts of the process have been implemented to run efficiently on a GPU. Extensive experimental results demonstrate that accurate and robust tracking is achievable at 15Hz. Thus, to the best of our knowledge, the proposed method is the first that simultaneously (a) provides accurate, continuous solutions to the problem of 3D tracking of hand articulations (b) does not require a complex hardware setup (c) relies solely on markerless visual data (d) is rather insensitive to illumination conditions and (e) runs in near real-time.
1.1 Related work
Moeslund et al. [14] provide a thorough review covering the general problem of visual human motion capture and analysis. Human body and human hand pose recovery are problems sharing important similarities such as the tree-like connectivity and the size variability of the articulated parts. A variety of methods have been proposed to capture human hand motion. Erol et al. [6] present a review of such methods. Based on the completeness of the output, they differentiate between partial and full pose estimation methods, further dividing the last class into appearance- and model-based ones.
Appearance-based methods typically establish a mapping from a set of image features to a discrete, finite set of hand model configurations [3, 19, 20, 22, 26]. The discriminative power of these methods depends on the invariance properties of the employed features, the number and the diversity of the postures to be recognized and the method used to derive the mapping. Due to their nature, appearance-based methods are well suited for problems such as hand posture recognition where a small set of known target hand configurations needs to be recognized. Conversely, such methods are less suited for problems that require an accurate estimation of the pose of freely performing hands. Moreover, generalization for such methods is achieved only through adequate training. On the positive side, training is performed offline and online execution is typically computationally efficient.
Model-based approaches [5, 7, 15, 16, 18, 23, 24] generate model hypotheses and evaluate them on the available visual observations. Essentially, this is performed by formulating an optimization problem whose objective function measures the discrepancy between the visual cues that are expected due to a model hypothesis and the actual ones. The employed optimization method must be able to evaluate the objective function at arbitrary points in the multidimensional model parameters space, so, unlike appearance-based methods, most of the computations need to be performed online. The resulting computational complexity is the main drawback of these methods. On the positive side, such methods do not require training and are also more easily extendable.
Another categorization can be defined, based on how partial evidence regarding the individual rigid parts of the articulated object contributes to the final solution. We differentiate among disjoint evidence methods that consider individual parts in isolation prior to evaluating them against observations [7, 18, 22, 24] and joint evidence methods [3, 5, 15, 16, 19, 20, 23, 26] that consider all parts in the context of full object hypotheses. Disjoint evidence methods usually have lower computational requirements than joint-evidence ones, but need to cope explicitly with the difficult problem of handling part interactions such as collisions and occlusions. In joint-evidence methods, part interactions are effortlessly treated but their computational requirements are rather high. Until recently, the only available jointevidence methods were appearance-based. As an example, Shotton et al. propose in [22] an appearance-based, disjoint evidence method for human body pose estimation with remarkable computational performance.
This paper presents a model-based method that treats 3D hand pose recovery as a minimization problem whose objective function is the discrepancy between the 3D structure and appearance of hypothesized 3D hand model instances, and visual observations of a human hand. Observations come from an off-the-shelf Kinect sensor. Optimization is performed through a variant of PSO tailored to the needs of the specific problem. Other versions of PSO have been employed in the past for human body pose tracking [9] and multicamerabased hand pose estimation [15].
Under the taxonomy of [6], the present work is a full, model-based pose estimation method that employs a single hypothesis. Furthermore, according to the categorization introduced earlier, it is a joint-evidence method. From a methodological point of view, the mostly related existing method [15] treats the problem of 3D hand pose estimation as an optimization problem that is solved through canonical PSO. However, the observations in [15] are 2D silhouettes of a hand extracted from a multicamera system. In the present work, the observation is the RGB plus depth images provided by a Kinect sensor. As a direct consequence, the objective function is different, the computational requirements are much smaller, the required camera setup is greatly simplified and the resulting system can be operational in situations where illumination conditions may vary substantially.
Another closely related work is that of Hamer et al. [7]. In both works the input is range data and a model-based approach is adopted. Hamer employs Belief Propagation which is well-suited for specific interdependency patterns among the parameters: the dependency graph must be a tree. Since the fingers usually interact (occlude or touch) with each other, special, explicit handling of such interactions is required. In our work, self-occlusions are naturally and effortlessly treated since we adopt a joint-evidence approach.
2 Tracking hand articulations based on the Kinect
The input to the proposed method (see Fig.1) is an image acquired using the Kinect sensor, together with its accompanying depth map. Skin color detection followed by depth segmentation is used to isolate the hand in 2D and 3D. The adopted 3D hand model comprises of a set of appropriately assembled geometric primitives. Each hand pose is represented as a vector of 27 parameters. Hand articulation tracking is formulated as the problem of estimating the 27 hand model parameters that minimize the discrepancy between hand hypotheses and the actual observations. To quantify this discrepancy, we employ graphics rendering techniques to produce comparable skin and depth maps for a given hand pose hypothesis. An appropriate objective function is thus formulated and a variant of PSO is employed to search for the optimal hand configuration. The result of this optimization process is the output of the method for the given frame. Temporal continuity is exploited to track the hand articulation in a sequence of frames. The remainder of this section describes these algorithmic steps in more detail.
2.1 Observing a hand
The input to the method is a 640x480 RGB color image of a hand and a corresponding depth image, as these are provided by the Kinect sensor [13]. Skin color is detected as in [2] and the resulting largest skin colored blob is kept for further consideration. A conservative estimation of the hands spatial extend is computed by dilating this blob with a circular mask of radius r = 5. Given the estimation of the 3D position of the tracked hand for the previous frame, skin colored 3D points that are within a preset depth range (25cm) from that estimation are kept, whereas the remaining depth map is set to zero. The observation model O = (os;od) that feeds the rest of the process consists of the 2D map os of the segmented skin color and the corresponding depth map od.
2.2 Modeling a hand
The employed hand model consists of a palm and five fingers. The palm is modeled as an elliptic cylinder and two ellipsoids for caps. Each finger consists of three cones and four spheres, except for the thumb which consists of an ellipsoid, two cones and three spheres. Similarly to [15] we build all the necessary geometric primitives for the hand using two basic 3D geometric primitives, a sphere and a cylinder, enabling a high degree of computational parallelism (see Sec. 2.5). The hand model is depicted in Fig. 1(d) with color-coded geometric primitives (yellow: elliptic cylinders, red: ellipsoids, green: spheres, blue: cones).
The kinematics of each finger is modeled using four parameters encoding angles, two for the base of the finger and two for the remaining joints. Bounds on the values of each parameter are set based on anatomical studies [1]. The global position of the hand is represented using a fixed point on the palm. The global orientation is parameterized using the redundant representation of quaternions. The resulting parameterization encodes a 26-DOF hand model with a representation of 27 parameters.
2.3 Evaluating a hand hypothesis
Having a parametric 3D model of a hand, the goal is to estimate the model parameters that are most compatible to the visual observations (Sec. 2.1). To do so, given a hand pose hypothesis h and camera calibration information C, a depth map rd(h;C) is generated by means of rendering. By comparing this map with the respective observation od, a “matched depths” binary map rm(h;C) is produced. More specifically, a pixel of rm is set to 1 if the respective depths in od and rd differ less than a predetermined value dm or if the observation is missing (signified by 0 in od), and 0 otherwise. This map is compared to the observation os, so that skin colored pixels that have incompatible depth observations do not positively contribute to the total score (Sec. 2.3, Eq.( 2)).
A distance measure between a hand pose hypothesis h and the observation maps O is established. This is achieved by a function E(h;O) that measures the discrepancy between the observed skin and depth maps O computed for a given frame and the skin and depth maps that are rendered for a given hand pose hypothesis h:
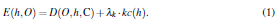
In Eq.(1), lk is a normalization factor. The function D in Eq.(1) is defined as
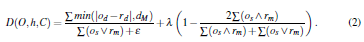
The first term of Eq.(2) models the absolute value of the clamped depth differences between the observation O and the hypothesis h. Unless clamping to a maximum depth dM is performed, a few large depth discrepancies considerably penalize an otherwise reasonable fit. This fact, in turn, creates large variations of the objective function’s value near the optimum, hindering the performance of any adopted optimization strategy. A small value e is added to the denominator of this term to avoid division by zero. The second term of Eq.(2) models the discrepancies between the skin-colored pixels of the model and the observation. l is a constant normalization factor. The sums are computed over entire feature maps.
The function kc in Eq.(1) adds a penalty to kinematically implausible hand configurations. An elaborate collision scheme was considered for kc, taking into account all possible pairs of relatively moving hand parts. Experimental results have demonstrated that for the majority of encountered situations, it suffices to penalize only adjacent finger interpenetration. Thus, in the current implementation: where Q denotes the three pairs of adjacent fingers, excluding the thumb, and f denotes the difference (in radians) between the abduction-adduction angles of those fingers in hypothesis h. In all experiments, l was set to 20 and of lk to 10. The depth thresholds were set to dm = 1cm and dM = 4cm.
2.4 Stochastic optimization through particle swarms
Particle Swarm Optimization (PSO) was introduced by Kennedy and Eberhart in [10, 11]. PSO is a stochastic, evolutionary algorithm that optimizes an objective function through the evolution of atoms of a population. A population is essentially a set of particles that lie in the parameter space of the objective function to be optimized. The particles evolve in runs which are called generations according to a policy which emulates “social interaction”.
Every particle holds its current position (current candidate solution and kept history) in a vector xk and its current velocity in a vector vk. Vector Pk stores the position at which each particle achieved, up to the current generation k, the best value of the objective function. Finally, the swarm as a whole, stores in vector Gk the best position encountered across all particles of the swarm. Gk is broadcast to the entire swarm, so every particle is aware of the global optimum. The update equations that reestimate each particle’s velocity and position in every generation k are

where w is a constant constriction factor [4]. In Eq. (3), c1 is called the cognitive component, c2 is termed the social component and r1; r2 are random samples of a uniform distribution in the range [0..1]. Finally, c1+c2 > 4 must hold [4]. In all performed experiments the values c1 = 2.8, c2 = 1.3 and  with
with  were used.
were used.
Typically, the particles are initialized at random positions and zero velocities. Each dimension of the multidimensional parameter space is bounded in some range. If, during the position update, a velocity component forces the particle to move to a point outside the bounded search space, a handling policy is required. A variety of alternative policies have been proposed in the relevant literature [8]. The “nearest point” method was chosen in our implementation. According to this, if a particle has a velocity that forces it to move to a point po outside the bounds of the parameter space, that particle moves to the point pb inside the bounds that minimizes the distance |po-pb|.
In this work, PSO operates in the 27-dimensional 3D hand pose parameter space. The objective function to be optimized (i.e., minimized) is E(O;h) (Eq. 1) and the population is a set of candidate 3D hand poses hypothesized for a single frame. Thus, the process of tracking a human hand requires the solution of a sequence of optimization problems, one for each acquired frame. By exploiting temporal continuity, the solution over frame Ft is used to generate the initial population for the optimization problem for frame Ft+1. More specifically, the first member of the population hre f for frame Ft+1 is the solution for frame Ft; The rest of the population consists of perturbations of href. The variance of these perturbations is experimentally determined as it depends on the anticipated jerkiness of the observed motion and the image acquisition frame rate. The optimization for frame Ft+1 is executed for a fixed amount of generations. After all generations have evolved, the best hypothesis hbest is dubbed as the solution for time step t+1.
The above described PSO variant successfully estimates the 6D global pose of the hand. However, the estimation of the 20 remaining parameters that are related to finger angles is not equally satisfactory. The swarm quickly converges to a point close to the optimum in a behavior that in the relevant literature [11] is termed “swarm collapse”. However the estimation of the parameters for the fingers often gets stuck to local minima. To overcome this problem and increase accuracy, we employed a PSO variant that performs randomization on the 20 dimensions corresponding to finger joint angles, similar to that suggested in [27]. More specifically, every ir generations, half of the particles are disturbed, each in a different, randomly chosen finger joint dimension dr. The value that is assigned to xt[dr] is a sample of the uniform distribution in the permitted range for dr. The value of ir was set to 3 generations in all experiments.
2.5 GPU acceleration
The most computationally demanding part of the proposed method is the evaluation of a hypothesis-observation discrepancy E(h;O) and, especially, its term D. The computation of D involves rendering, pixel-wise operations between an observation and a hypothesis map and summation over the results. We exploit the inherent parallelism of this computation by performing these operations on a GPU. Furthermore, by evaluating simultaneously the function D for many hypotheses hi (i.e., for all the particles of a PSO generation), we minimize the overhead of communication between the CPU and the GPU. Hardware instancing is employed to accelerate the rendering process, exploiting the fact that the hand model is made up of transformed versions of the same two primitives (a cylinder and a sphere). The pixel-wise operations between maps are inherently parallel and the summations of the maps are performed efficiently by employing a pyramidal scheme. More details on the GPU implementation are provided in [12].
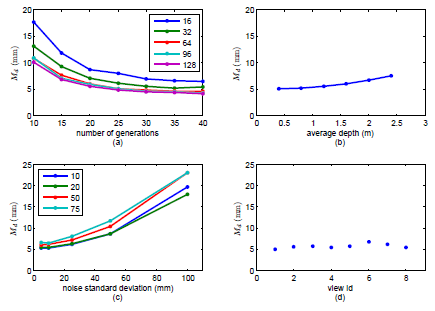
Figure 2: Quantitative evaluation of the performance of the method with respect to (a) the PSO parameters (b) the distance from the sensor (c) noise and (d) viewpoint variation.
3 Experimental evaluation
The experimental evaluation of the proposed method was based on synthetic data with ground truth information and on real-world sequences obtained by a Kinect sensor. The proposed method runs on a computer equipped with a quad-core Intel i7 950 CPU, 6 GBs RAM and an Nvidia GTX 580 GPU with 1581GFlops processing power and 1.5 GBs memory. On this system, the average frame rate is 15Hz. As discussed in [12] there is still room for performance improvements.
Synthetic data were used for the quantitative evaluation of the proposed method. This is a common approach in the relevant literature [7, 15] because ground truth data for real-world image sequences is hard to obtain. The employed synthetic sequence consists of 360 consecutive hand poses that encode everyday hand motions as simple as waving and as complex as object grasping. Rendering was used to synthesize the required input O for each considered hand pose. To quantify the accuracy in hand pose estimation, we adopt the metric used in [7]. More specifically, the distance between corresponding phalanx endpoints in the ground truth and in the estimated hand model is measured. The average of all these distances over all the frames of the sequence constitutes the resulting error estimate D.
Several experiments were carried out to assess the influence of several factors to the performance of the method. Figure 2(a) illustrates the behavior of the method with respect to the PSO parameters (number of generations and particles per generation). The product of these parameters determines the computational budget of the proposed methodology, as it accounts for the number of objective function evaluations. The horizontal axis of the plot denotes the number of PSO generations. Each plot of the graph corresponds to a different number of particles per generation. Each point in each plot is the median Md of the error D for 20 repetitions of an experiment run with the specific parameters. A first observation is that Md decreases monotonically as the number of generations increase. Additionally, as the particles per generation increase, the resulting error decreases. Nevertheless, employing more that 25 generations and more than 64 particles results in insignificant improvement of the method’s accuracy. The gains, if any, are at most 0:5mm. For this reason, the configuration of 64 particles for 25 generations was retained in all further experiments.
Another investigation considered the effect of varying the distance of the hand from the hypothesized sensor. This explores the usefulness of the method in different application scenarios that require observations of a certain scene at different scales (e.g., close-up views of a hand versus distant views of a human and his/her broader environment). To do this, we generated the same synthetic sequences at different average depths. The results of this experiment are presented in Fig. 2(b). At a distance of half a meter the error is equal to 5mm. As the distance increases, the error also increases; Interestingly though, it doesn’t exceed 7.5mm even at an average distance of 2.5m.
5mm even at an average distance of 2.5m. The method was also evaluated with respect to its tolerance to noisy observations. Two types of noise were considered. Errors in depth estimation were modeled as a Gaussian distribution centered around the actual depth value with the variance controlling the amount of noise. Skin-color segmentation errors were treated similarly to [19], by randomly flipping the label (skin/non-skin) of a percentage of pixels in the synthetic skin mask. Figure 2(c) plots the method’s error in hand pose estimation for different levels of depth and skin segmentation error. As it can be verified, the hand pose recovery error is bounded in the range [5mm..25mm], even in data sets very heavily contaminated with noise.
We also assessed the accuracy in hand pose estimation with respect to viewpoint variations. This was achieved by placing the virtual camera at 8 positions dispersed on the surface of a hemisphere placed around the hypothesized scene. The data points of Fig. 2(d) demonstrate that viewpoint variations do not significantly affect the performance of the method.
Several long real-world image sequences were captured using the PrimeSense Sensor Module of OpenNI [17]. The sequences exhibit hand waving, palm rotations, complex finger articulation as well as grasp-like hand motions. The supplemental material accompanying the paper1 provides videos with the results obtained in two such sequences (1341 and 1494 frames, respectively). Indicative snapshots are shown in Fig. 3. As it can be observed, the estimated hand model is in very close agreement with the image data, despite the complex hand articulation and significant self occlusions.

Figure 3: Indicative results on real-world data.
Finally, besides tracking, we tested the capability of the proposed method to perform automatic hand model initialization, i.e., single-frame hand pose estimation. Essentially, this boils down to the capability of PSO to optimize the defined objective function even when parameter ranges are very broad. To do so, the proposed algorithm run many times, each initialized at different hand positions and orientations close to the observed hand (the largest skin color blob). The best scoring hypothesis of this process was kept as the recovered pose. To assess the method, a set of 45 frames was selected at regular intervals from a real-world sequence and each hand pose recognition was performed 20 times. For the quantitative assessment of the hand pose recognition accuracy, we used as a reference the hand model parameters that were recovered from an experiment that tracked the hand articulation over the whole sequence. Figure 4 shows the histogram of estimation error Md for all the performed (20x45) experiments. As it can be verified, in 74% of them, the estimated pose deviated 4cm or less from the tracked pose. The secondary histogram peak around 8cm corresponds to some ambiguous poses for which sometimes the mirrored pose was estimated.
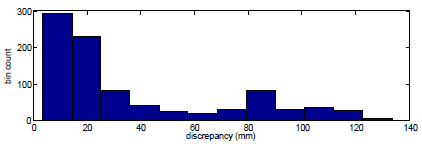
Figure 4: Performance of single-frame hand pose estimation.
4 Discussion
We proposed a novel model-based method for efficient full DOF hand model initialization and tracking using data acquired by a Kinect sensor. The combination of (a) a careful modeling of the problem (b) a powerful optimization method (c) the exploitation of modern GPUs and, (d) the quality of the data provided by the Kinect sensor, results in a robust and efficient method for tracking the full pose of a hand in complex articulation. Extensive experimental results demonstrate that accurate and robust 3D hand tracking is achievable at 15Hz. Thus, it is demonstrated that model-based joint-evidence tracking is feasible in near real-time. It is important to note that there is no inherent limitation that prevents the proposed method to be used on any other type of depth images resulting, for example, from standard dense stereo reconstruction methods.
Acknowledgments
This work was partially supported by the IST-FP7-IP-215821 project GRASP. The contribution of Konstantinos Tzevanidis and Pashalis Padeleris, members of CVRL/FORTH, is gratefully acknowledged.
References
1. Irene Albrecht, J?rg Haber, and Hans-Peter Seidel. Construction and Animation of Anatomically Based Human Hand Models. In Eurographics symposium on Computer animation, page 109. Eurographics Association, 2003.
2. Antonis A. Argyros and Manolis Lourakis. Real-time Tracking of Multiple Skincolored Objects with a Possibly Moving Camera. pages 368–379. Springer, 2004.
3. Vassilis Athitsos and Stan Sclaroff. Estimating 3D Hand Pose From a Cluttered Image. CVPR, pages II–432–9, 2003.
4. Maurice Clerc and James Kennedy. The Particle Swarm - Explosion, Stability, and Convergence in a Multidimensional Complex Space. Transactions on Evolutionary Computation, 6(1):58–73, 2002.
5. Martin De La Gorce, Nikos Paragios, and David J. Fleet. Model-based Hand Tracking With Texture, Shading and Self-occlusions. CVPR, (June):1–8, June 2008.
6. Ali Erol, George Bebis, Mircea Nicolescu, Richard D. Boyle, and Xander Twombly. Vision-based Hand Pose Estimation: A review. Computer Vision and Image Understanding, 108(1-2):52–73, 2007.
7. Henning Hamer, Konrad Schindler, E. Koller-Meier, and Luc Van Gool. Tracking a Hand Manipulating an Object. In ICCV, 2009.
8. Sabine Helwig and Rolf Wanka. Particle Swarm Optimization in High-Dimensional Bounded Search Spaces. In Swarm Intelligence Symposium, pages 198–205. IEEE, 2007.
9. Vijay John, Spela Ivekovic, and Emanuele Trucco. Articulated Human Motion Tracking with HPSO. International Conference on Computer Vision Theory and Applications, 2009.
10. James Kennedy and Russ Eberhart. Particle Swarm Optimization. In International Conference on Neural Networks, volume 4, pages 1942–1948. IEEE, January 1995.
11. James Kennedy, Russ Eberhart, and Shi Yuhui. Swarm intelligence. Morgan Kaufmann, 2001.