Українська   Русский
DonNTU   Masters' portal

Abstract

Content

Introduction

One of the most difficult problems of image processing is the selection of the contour of objects for their further recognition. The key is the task of identifying lines that run along the borders of homogeneous areas. One of the most difficult problems of image processing is the selection of the contour of objects for their further recognition. The key is the task of identifying lines that run along borders. homogeneous areas.

Allocation of borders is based on algorithms that determine a sharp change in brightness in an image. The result of the execution of the boundary selection algorithms should be a certain number of connected curves, which display the boundaries of the object. In most cases, the borders on the images are less pronounced. contrast, so the currently existing algorithms and operators do not provide efficiency the result. Often, processing results vary from discontinuities in contours and lines. (fragmentation) to the complete absence of a border.

One of the most complex applications in this area is the selection of lines on the palm. Selecting the outline of the palm is usually not a difficult task, and highlighting the lines on it is enough nontrivial operation, since due to the low contrast of the lines in relation to their surroundings and the abundance of interference (noise) there are breaks, false lines or their complete absence.

1. Relevance of the topic

The recognition of visual images is one of the most important components of control systems and information processing, automated systems and decision-making systems. Tasks related to classification and identification of objects, phenomena and signals, characterized by a finite set Some properties and attributes arise in such industries as robotics, information retrieval, monitoring and analysis of visual data, research of artificial intelligence. Currently in In the production, handwriting recognition systems, car numbers, fingerprints or human faces that are used in the interfaces of software products, security systems and personal identification, as well as other applications.

However, the actual problem recognized by the scientific community is the recognition of objects on noisy images, which complicates the definition of object boundaries and further processing accordingly.

The urgency of this problem is especially high in industries where pattern recognition is used in the natural environment (video surveillance, data analysis of monitoring cameras, robotic visual system), where the visual sensor can have an arbitrary limited viewing angle relative to the desired to the object.

2. The purpose and objectives of the study, the planned results

The aim of the study is to develop an algorithm for swarm optimization for recognition problems on noisy images

Suppression of digital stochastic noise during post-processing is performed by averaging pixel brightness over some group of pixels, which the algorithm considers "similar". Usually, this deteriorates the detail. image, it becomes more "soapy". In addition, there may be false details that were not on the original scene. For example, if the algorithm does not look for "similar" pixels far enough, then fine-grained and medium-grained noise can be suppressed, and a weak, but still quite noticeable unnatural "large" noise will remain visible.

The main objectives of the study:

  1. Development of the algorithmic base for the presented model, which includes the recognition algorithm images.
  2. The implementation of an algorithmic complex in the form of a computer program.
  3. Evaluation of the performance of the developed method and criteria for achieving the goal.
  4. Assessment of the effectiveness of the developed method in comparison with modern alternative methods recognition

3. Review of research and development

Since the recognition of objects in images is a very hot topic, problems Recognition is widely investigated by both our and foreign scientists.

3.1 Overview of international sources

The work of Gonzalez and Woods [1] dedicated to image segmentation, their presentation and description. The detail of the presentation of all questions is quite high. This book is the best suitable for additional study of this topic in general.

The work is dedicated to Lakshmi and Sankakanyaanana tekstuam [2]. Logics The presentation corresponds to our course, but the volume is significantly larger and the presentation is more detailed and deeper. Since the topic texture analysis is described by us extremely briefly, this chapter of can also be recommended entirely as a material for additional self-study.

In the work of A. Zuev [3] examines the image segmentation task (in the broad sense) respectively in the context of clustering (partitioning the sample into classes) and probabilistic optimization (maximum of a posteriori probability and Bayesian approach).

4. Optimization by a swarm of particles

The Particle Swarm Optimization (PSO) algorithm is based on socio-psychological behavioral model of the crowd. The development of the algorithm was inspired by tasks such as simulation of the behavior of birds in the flock and fish in the school. The goal was to discover the basic principles thanks to which, for example, birds in a flock behave surprisingly synchronously, changing directions as if by command its movement, so that the pack moves as a whole. To modern times the concept of the swarm algorithm particles has developed into a highly efficient optimization algorithm, often competing with the best modifications of the genetic algorithm. There are a significant number of particle swarm algorithms. AT canonical algorithm proposed in 1995 by Kennedy (J. Kennedy) and Eberhart (R. Eberhart), with determining the next position of a particle, information on the best particle from among its "Neighbors", as well as information about this particle at the iteration of the algorithm, at which this particle matched the best value of the fitness function. There are a large number of modifications of this algorithm. For example, the FIPS modification takes the fitness value into account when determining the next particle position. functions corresponding to all particles of the population.

Below are the PSO canonical algorithm, the most well-known modifications of the canonical algorithm, The notion of a neighborhood topology is defined. In addition, the main topologies used in computational practice, a review of PSO algorithms with a dynamic topology of particle proximity is given, A hybrid algorithm based on particle swarm and simulated annealing is presented. At the end of the paragraph is given example of using the PSO algorithm.

5. Automatic clustering using particle swarm optimization

5.1 Basic Idea

The basic idea of the swarm intelligence algorithms is that a set of individuals can collaborate in a decentralized manner, increasing your productivity. So the goal is to find mechanisms that can model complex systems, and represent them in a formal way

5.2 Optimization by a swarm of particles

Optimization of particle pianos is a form of stochastic optimization based on swarms. simplistic, social agents [4]. Primary particle optimization swarm optimization algorithms by m-dimensional space U using a set of agents. In this lattice, the agent (particles) i occupy the position xi (t) = {xi, j (t) | j = 1, ..., m} and has speed vi (t) = {vi, j (t) | j = 1, ..., m} at time t, with a 1: 1 ratio (both xi (t) and vi (t) contain a set component {j = 1, ..., m}, mapped to coordinates in U). A simple algorithm PSO [5] works as follows way: at the initialization stage, each agent takes positions around x (0) = xmin + r (xmax -xmin), and speeds are set to 0 (xmin and xmax are the minimum and maximum values in U, and r is real number between 0 and 1). Secondly, the algorithm enters the search phase. The search phase consists of Next steps: Better cognitive / global position update and speed / position update.

At the cognitive update stage, each agent sets a value for the current (local) the best position is yi (t), which it directly observed. Updated local optimizer agent yi (t +1) according to the equation:

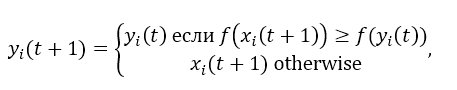
Updated local optimizer agent

whereas f (xi (t)) is a fitness function that evaluates the goodness of a decision based on positions xi (t).

In contrast, the global update step sets the best possible position at each iteration Yi observed at any agent. The following equation represents the choice of the best global position:

Choosing the best global position

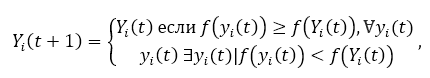
The speed or position update step selects new values for position xi (t +1) and speed vi (t +1) using the equations:

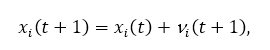
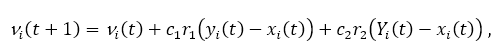
Speed Update Step
Speed Update Step

where the parameters c1 and c2 are used to direct the search between the local (cognitive components) and social (global components) of observation. r1, r2 ∈ [0,1] are random parameters which introduce stochastic weight in the search. Finally, the algorithm stops until it is reached. point of convergence.

Proposed convergence criterion proposed in [6]; it consists in (f (Yi (t)) - f (Yi (t-1))) / f (Yi (t)) is less than the small constant ε for a given number of iterations. It is important to note that each particle in this multi-agent system shares its knowledge (global best position) with all other particles with using neighborhood topology.

It has been proposed several topologies [7] (m. E. star, ring, clusters of von Neumann, etc.). Difference between districts is how quickly or slowly (depending on connectivity) knowledge spread through the swarm.

Further improvements have been proposed for the basic algorithm PSO [8,9]: Velocity clamp, inertial weight and coefficient of contraction. All PSO-based algorithms in this study were performed with using the contraction coefficient (the most reliable mechanism).

Speed ratio The weakness of the optimization algorithms for the main role of particles is that rises quickly to unsuitable values. High speed leads to large (in this case, particles may even go beyond the boundaries of the search space). This is especially true for particles occupying higher positions. Speed clamping is a simple limitation that imposes a maximum speed. On the equation This rule is depicted.

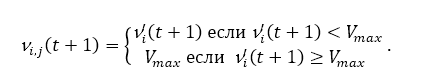
Speed coefficient

Obviously, large Vmax values facilitate exploration (small ones prefer exploitation). Vmax often is fraction δ domain space for each dimension j in the search space U. Following equation represents this adjustment.

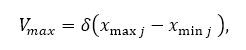
Velocity coefficient with adjustment

while xmaxj and xminj are the maximum and minimum values, respectively.

Weight inertia. Inertial weight is a limitation that aims to control the trade-off between exploration and exploitation in a more direct way. The equation introduces the inertial weight w, which affects to update speed.

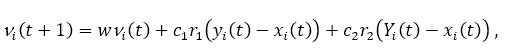
Inertia Weight

w ≥ 1 leads to an increase in speed over time (study), w < 1 reduces the speed with time (in favor of operation). According to [10] values w = 0,7298, c1 = c2 = 1.49618 proved good the results are empirically, although in many cases they are a dependent problem.

The coefficient of contraction. A similar method of inertial weight was proposed in [11], denominated contraction coefficient. The equation defines a new speed update mechanism.

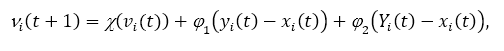
Narrowing Ratio

where φ = φ1 + φ2, φ1 = c1r1, φ2 = c2r and

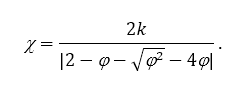
Narrowing Ratio

It is important to note that φ ≥ 4 и k ∈ [0,1] are necessary restrictions for installation χ in the range [0,1].

6. Multi-agent clustering PSO

Previously were presented the theoretical foundations required in which the new AutoCPB relies. In that The section will look in detail at our multi-agent system for clustering. One of the main problems with PSO algorithms is that they tend to get into suboptimal solutions due to the lack of diversity in the swarm. One of our ambitions is to find a mechanism for improve diversity. Improving the initial algorithm PSO [12] is to use either memetic approach or hybridization another method of swarm intelligence [13]. AutoCPB Provided - Hybrid Heuristic algorithm we decided develop preliminary prototype algorithms. We begin to introduce a simplified swarm-based clustering method, and then we gradually introduce more thoughtful development

6.1 Clustering PSO

We implemented a simple clustering algorithm, denoted ClusterP, which was proposed in [14]. This method combines PSO and K-tools for grouping data.

The data set D = {d1, m, d2, m, ..., dn, m} determines the number of components m and instances n in the search space U. Thus, each dumum di, j ∈ D can be viewed as a point in U. Since the goal is to find the set of k desired clusters C containing each element of D; it is easy to understand that the main problem is to find the set O = {o1, o2, ..., ok} centroids that minimize the fitness function (Euclidean distance) with respect to each point in D. In clusterP each agent pl ∈ P is a solution with a set of positions Ol = {ol, j | j = one, ..., k}. The algorithm presented in Figure 1 shows the ClusterP method.

ClouserP Algorithm

Figure 1 - ClouserP Algorithm

ClusterP works like this: it gets the data D and the integer k. First, it blends each agent p in the environment, each of which contains a set of centroids O (line 1). Then, he assigns each di record to Ch cluster, if the distance with its center of gravity (di, oh) is equal to the minimum (lines 3-8). It then takes a cognitive and global position (lines 9-12), and updates each of its velocities and positions of centroids (lines 13-16). The algorithm stops after a fixed number. iterations or if there is no significant progress is carried out in accordance with the function of fitness.

6.2 Automatic PSO Clustering

ClusterP was extended in [15], to automatically find the optimal amount clusters.

The new method is called AutoCP. It starts with cluster number k (k ≤ n), and it removes inconsistent clusters.

The form for detecting unmatched clusters is described as follows: first, for each cluster Cj calculate its weight Wj = ∑| Cj |q = 1 dist (oj, dq) as the sum of the distances from the center oj to him points qj, where qj = oj. Immediately, all the W weights from the clusters are sorted. Then we normalize all weights wj relative to the cluster with the smallest value Ws, so that the set of local thresholds becomes th = {thj | j = 1, ..., k, thj = Ws / Wj, Ws = argminw ∈ W (w)}. Finally, the Cj cluster is declared uncoordinated if its threshold tj is below the global threshold T, then T is in the range [0,1]. Algorithm presented in Figure 2.

Improved ClouserP Algorithm

Figure 2 - Improved ClouserP Algorithm

As mentioned earlier, AutoCP simply adds a mechanism for ClusterP to automatically detect clusters without further modification (lines 6-15). At the end of each iteration, we select and discard. unmatched clusters.

Findings

One of the most difficult problems of image processing is the selection of the contour of objects for their further recognition. The key is the task of identifying lines that run along the borders of homogeneous areas.

Since in most cases the borders on the images are not so contrasting, therefore the existing на данный момент алгоритмы и операторы не обеспечивают эффективность получаемого результата. Часто результат обработки варьируется от разрывов контуров и линий (фрагментированность) до полного отсутствия границы. Одним из наиболее перспективных, на мой взгляд, является подход, основанный на выделении контуров на малоконтрастных и размытых изображениях на основе фрактальной фильтрации. Фракталы более наглядно выделяют контуры, чем другие операторы, но они ориентированы на обработку малоконтрастных изображений в целом, а не на выделение отдельных линий и границ.

В этой работе была описана техники разведки роя, а именно: рой частиц оптимизации. Были подробно описан алгоритм, основанный на этой парадигме. Новые алгоритмы улучшают базовый кластерный метод, который на самом деле основано на K-значении.

References

  1. Gonzalez D., Woods D., Hildreth E. Theory of edge detection/Dslash Proc. R. Soc. (London). 2009. B207. 187 – 217c.
  2. Lakshmi S, Sankaranarayanan V. (2010) A Study of edge detection techniques for segmentation computing approaches, Computer Aided Soft Computing Techniques for Imaging and Biomedical Applications. - P. 35–41.
  3. Zuev A.A. Contour detection methods on images / А.А. Zuev, G.E. Necheporenko // MicroCAD International Scientific Conference: Section No. 8 - Microprocessor-based technology in automation and application - NTU KPI, 2012. - P. 108.
  4. Kennedy, J., Ebenhart, R.: Particle Swarm Optimization. In: Proceedings of the 1995 IEEE Int. Conf. on Neural Networks, pp. 1942–1948 (1995)
  5. Passino, K.: Biomimicry of bacterial foraging for distributed optimization and control. Control Systems Magazine, 52–67 (2002)
  6. Engelbrecht, A.: Fundamentals of Computational Swarm Intelligence. Wiley, Chichester (2005)
  7. Heylighen, F., Joslyn, C.: Cybernetics and second-order cybernetics. Encyclopedia of Physical Science and Technology. Academic Press, New York (2001)
  8. Bergh, F.: An analysis of particle swarm optimizers. PhD Thesis, University of Pretoria, South Africa (2002)
  9. Van der Merwe, D., Engelbrecht, A.: Data Clustering using particle swarm optimization. In: The 2003 congress on Evolutionary Computation, vol. 1, pp. 215–220 (2003)
  10. Biswas, A., Dasgupta, S.: Synergy of PSO and bacterial foraging optimization: A comprehensive study on. Advances in Soft Computing Series, pp. 255–263. Springer, Heidelberg (2007)
  11. Holdsworth B. Digital logic design / B. Holdsworth, C. Woods. – Prentice Hall, 2002. – 519 pp.
  12. Abraham, A., Roy, S.: Swarm intelligence algorithms for data clustering. Chp. 12, 279–313 (2008)
  13. Asuncion, A., Newman, D.: UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences (2007)
  14. Clerc, M., Kennedy, J.: The particle swarm: Explosion, stability and convergence. IEEE Transactions on Evolutionary Computation 6, 58–73 (2002)
  15. Zhan, Z-H.; Zhang, J. Adaptive Particle Swarm Optimization. IEEE Transactions on Systems, Man, and Cybernetics. 39 (6): 1362–1381