Українська   English
ДонНТУ   Портал магистров

Содержание

Введение

Одной из наиболее сложных проблем обработки изображений является выделение контура объектов для их дальнейшего распознавания. Ключевой является задача выделения линий, проходящих на границах однородных областей.Одной из наиболее сложных проблем обработки изображений является выделение контура объектов для их дальнейшего распознавания. Ключевой является задача выделения линий, проходящих на границах однородных областей.

Выделение границ основывается на алгоритмах, которые определяют резкое изменение яркости на изображении. Результатом выполнения алгоритмов выделения границ должно быть некоторое количество связанных кривых, которые отображают границы объекта. В большинстве случаев границы на изображениях выражены не столь контрастно, поэтому существующие на данный момент алгоритмы и операторы не обеспечивают эффективность получаемого результата. Часто результат обработки варьируется от разрывов контуров и линий (фрагментированность) до полного отсутствия границы.

Одной из наиболее сложных прикладных задач в данной области является выделение линий на ладони. Выделение контура ладони обычно не является сложной задачей, а выделение линий на ней – достаточно нетривиальная операция, т.к. из-за низкой контрастности линий по отношению к их окружению и обилие помех (шума) возникают разрывы, ложные линии или полное их отсутствие.

1. Актуальность темы

Распознавание визуальных образов представляет собой один из важнейших компонентов систем управления и обработки информации, автоматизированных систем и систем принятия решений. Задачи, связанные с классификацией и идентификацией предметов, явлений и сигналов, характеризующихся конечным набором некоторых свойств и признаков, возникают в таких отраслях как робототехника, информационный поиск, мониторинг и анализ визуальных данных, исследования искусственного интеллекта. В настоящий момент в производстве широко используются системы распознавания рукописного текста, автомобильных номеров, отпечатков пальцев или человеческих лиц, находящие применение в интерфейсах программных продуктов, системах безопасности и идентификации личности, а также в других прикладных целях.

Однако, актуальной проблемой, признанной научным сообществом, остается распознавание изображенных объектов на зашумлённых изображениях, что усложняет определение границ объекта и дальнейшей обработки соотвественно.

Актуальность данной проблемы особенно высока в отраслях, где распознавание образов применяется в естественной среде (видеонаблюдение, анализ данных камер мониторинга, робототехнические зрительные системы), где зрительный сенсор может иметь произвольный ограниченный угол обзора по отношению к искомому объекту.

2. Цель и задачи исследования, планируемые результаты

Целью исследования является разработка алгоритма роевой оптимизации для задач распознавания на зашумленных изображениях

Подавление цифрового стохастического шума при постобработке проводится усреднением яркости пикселя по некоторой группе пикселей, который алгоритм считает "похожими". Обычно при этом ухудшается детальность изображения, оно становится более "мыльным". Кроме этого, могут проявится ложные детали, которых не было на исходной сцене. Например, если алгоритм будет искать "похожие" пиксели недостаточно далеко, то мелкозернситый и среднезернистый шум может быть подавлен, а слабый, но всё равно довольно заметный неестественный "крупный" шум останется видимым.

Основные задачи исследования:

  1. Разработка алгоритмической базы для представленной модели, включающей в себя алгоритм распознавания изображений.
  2. Реализация алгоритмического комплекса в виде программы для ЭВМ.
  3. Оценка производительности разработанного метода и критериев достижения поставленной цели.
  4. Оценка эффективности разработанного метода в сравнении с современными альтернативными методами распознавания

3. Обзор исследований и разработок

Поскольку распознавание объектов на изображениях является очень актуальной темой, то проблемы распознавания широко исследованы как нашими, так и иностранными учеными.

3.1 Обзор международных источников

Работе Гонсалеса и Вудса [1] посвящена сегментации изображений, их представлению и описанию. Подробность изложения всех вопросов достаточно высокая. Данная книга наилучшим образом подходит для дополнительного изучения данной темы в целом.

Работа Лакшми и Санкаканяанана посвящена текстуам [2]. Логика изложения соответствует нашему курсу, но объем существенно больше и изложение подробнее и глубже. Поскольку тема текстурного анализа описана нами чрезвычайно кратко, данная глава из также может быть рекомендована целиком в качестве материала для дополнительного самостоятельного изучения.

В работе Зуева А.А. [3] рассматривается задача сегментации изображения (в широком смысле) соответственно в контексте кластеризации (разбиения выборки на классы) и вероятностной оптимизации (максимума апостериорной вероятности и байесовского подхода).

4. Оптимизация роем частиц

В основу алгоритма оптимизации роем частиц (Particle Swarm Optimization, PSO) положена социально-психологическая поведенческая модель толпы. Развитие алгоритма инспирировали такие задачи, как моделирование поведения птиц в стае и рыб в косяке. Целью было обнаружить базовые принципы, благодаря которым, например, птицы в стае ведут себя удивительно синхронно, меняя как по команде направления своего движения, так что стая движется как единое целое. К современному времени концепция алгоритма роя частиц развилась в высокоэффективный алгоритм оптимизации, часто составляющий конкуренцию лучшим модификациям генетического алгоритма. Существует значительное число алгоритмов роя частиц. В каноническом алгоритме, предложенном в 1995 г. Кеннеди (J. Kennedy) и Эберхартом (R. Eberhart), при определении следующего положения частицы учитывается информация о наилучшей частице из числа ее «соседей», а также информация о данной частице на той итерации алгоритма, на которой этой частице соответствовало наилучшее значение фитнес-функции. Известно большое число модификаций данного алгоритма. Например, модификация FIPS при определении следующего положения частицы учитывает значения фитнес функции, соответствующие всем частицам популяции.

Ниже представлены канонический алгоритм PSO, наиболее известные модификации канонического алгоритма, определено понятие топологии соседства частиц. Кроме того, рассмотрены основные топологии, используемые в вычислительной практике, дан обзор алгоритмов PSO с динамической топологией соседства частиц, представлен гибридный алгоритм на основе роя частиц и имитации отжига. В завершении параграфа приведен пример использования алгоритма PSO.

5. Автоматическая кластеризация с использованием оптимизации роя частиц

5.1 Основная идея

Основная идея алгоритмов рой-интеллекта заключается в том, что набор индивидуумов могут сотрудничать децентрализованным образом, повышая свою производительность. Таким образом, цель найти механизмы, которые могут моделировать сложные системы, и представлять их в формальном пути

5.2 Оптимизация роем частиц

Оптимизация роялей частиц представляет собой форму стохастической оптимизации, основанной на роях упрощенных, социальных агентов [4]. Первичные алгоритмы оптимизации рой частиц поиск по m-мерному пространству U с помощью набора агентов. В этой решетке агент (частицы) i занимают положение xi (t) = {xi, j (t) | j = 1, ..., m} и имеет скорость vi (t) = {vi, j (t) | j = 1, ..., m} в момент времени t, с соотношением 1: 1 (оба xi (t) и vi (t) содержат набор компонент {j = 1, ..., m}, отображаемых в координаты в U). Простой алгоритм PSO [5] работает следующим образом: на этапе инициализации каждый агент принимает позиции вокруг x (0) = xmin + r (xmax -xmin), а скорости устанавливаются на 0 (xmin и xmax - минимальная и максимальная величины в U, а r - действительное число между 0 и 1). Во-вторых, алгоритм входит в фазу поиска. Фаза поиска состоит из следующих шагов: Лучшее обновление когнитивной / глобальной позиции и скорость / положение обновление.

На этапе когнитивного обновления каждый агент устанавливает значение для текущего (локального) наилучшего положение yi (t), которое оно непосредственно наблюдало. Обновлен локальный оптимизатор агента yi (t +1) согласно уравнению:

Обновлен локальный оптимизатор агента

тогда как f (xi (t)) является функцией пригодности, которая оценивает доброту основанного на решении на позиции xi (t).

Напротив, глобальный шаг обновления задает на каждой итерации наилучшее возможное положение Yi наблюдается у любого агента. Следующее уравнение отображает выбор наилучшего глобального положения:

Выбор наилучшего глобального положения

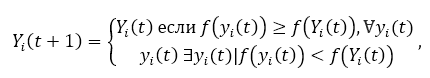
Шаг обновления скорости или положения выбирает новые значения для позиции xi (t +1) и скорость vi (t +1), используя уравнения:

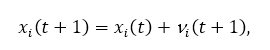
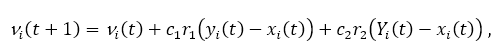
Шаг обновления скорости
Шаг обновления скорости

где параметры c1 и c2 используются для направления поиска между локальными (когнитивными компонент) и социальные (глобальные компоненты) наблюдения. r1, r2 ∈ [0,1] являются случайными параметрами которые вводят стохастический вес в поиске. Наконец, алгоритм останавливается пока не будет достигнута точка сходимости.

Предлагаемый критерий сходимости предлагается в [6]; он заключается в (f (Yi (t)) - f (Yi (t-1))) / f (Yi (t)) меньше малой константы ε для заданного числа итераций. Важно отметить, что каждая частица в этой многоагентной системе делится его знание (глобальное лучшее положение) со всеми другими частицами с помощью окрестности топология.

Было предложено несколько топологий [7] (т. Е. Звезда, кольцо, кластеры, фон Нейман, и т.д.). Разница между районами заключается в том, как быстро или медленно (в зависимости от связность) знания распространяются через рой.

Дальнейшие усовершенствования были предложены для базового алгоритма PSO [8,9]: Velocity зажим, инерционный вес и коэффициент сужения. Все алгоритмы на основе PSO в это исследование было выполнено с использованием коэффициента сужения (наиболее надежного механизма).

Скоростной коэффициент. Слабостью алгоритмов оптимизации основных ролей частиц является что скорость быстро возрастает до неподходящих значений. Высокая скорость приводит к большим (в этом случае частицы могут даже выйти из границ поиска пространство). Это особенно справедливо для частиц, занимающих высшие позиции. Зажим скорости является простым ограничением, налагающим максимальную скорость. На уравнении изображено это правило.

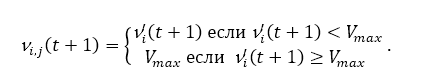
Скоростной коэффициент

Очевидно, что большие значения Vmax облегчают разведку (маленькие предпочитают эксплуатацию). Vmax часто является дробью δ доменного пространства для каждого измерения j в поиске пространство U. Следующее уравнение представляет эту корректировку.

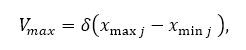
Скоростной коэффициент с корректировкой

тогда как xmaxj и xminj представляют собой максимальную и минимальную величины соответственно.

Вес инерции. Инерционный вес является ограничением, которое нацелено на контроль компромисса между разведкой и эксплуатацией более прямым образом. Уравнение вводит инерционный вес w, который влияет на обновление скорости.

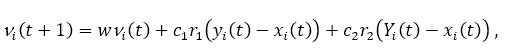
Вес инерции

w ≥ 1 приводит к увеличению скорости с течением времени (исследование), w < 1 уменьшает скорости со временем (в пользу эксплуатации). Согласно [10] значения w = 0,7298, c1 = c2 = 1.49618 доказали хорошие результаты эмпирически, хотя во многих случаях они являются проблемой зависимый.

Коэффициент сужения. Аналогичный метод инерционного веса был предложен в [11], деноминированный коэффициент сужения. Уравнение определяет новое обновление скорости механизм.

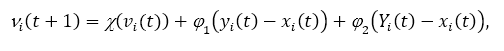
Коэффициент сужения

где φ = φ1 + φ2, φ1 = c1r1, φ2 = c2r2 и

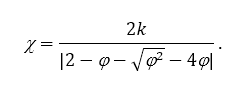
Коэффициент сужения

Важно заметить, что φ ≥ 4 и k ∈ [0,1] являются необходимыми ограничениями для установки χ в диапазоне [0,1].

6. Многоагентная кластеризация PSO

Ранее были представили теоретические основы, необходимые, в которых новый AutoCPB полагается. В этом разделе подробно рассмотрим нашу многоагентную систему для кластеризации. Одной из основных проблем, связанных с алгоритмами PSO, является то, что они имеют тенденцию попасть в субоптимальные решения из-за отсутствия разнообразия в рое. Один из наши амбиции - найти механизм для улучшения разнообразия. Улучшение исходного алгоритма PSO [12] заключается в использовании либо memetic подхода или гибридизации с другим методом разведки роя [13]. При условии AutoCPB – гибридный эвристический алгоритм, мы решили разработать предварительные прототипные алгоритмы. Мы начинаем вводить упрощенный метод кластеризации на основе рой, а затем мы постепенно представляем более продуманные разработки

6.1 Кластеризация PSO

Мы реализовали простой алгоритм кластеризации, обозначенный ClusterP, который был предложенный в [14]. Такой метод объединяет PSO и K-средства для группировки данных.

Набор данных D = {d1, m, d2, m, ..., dn, m} определяет число компонентов m и экземпляров n в пространстве поиска U. Таким образом, каждое dumum di, j ∈ D можно рассматривать как точку в U. Поскольку цель состоит в том, чтобы найти множество k желаемых кластеров C, содержащих каждый элемент из D; легко понять, что основная проблема состоит в том, чтобы найти множество O = {o1, o2, ..., ok} центроидов, которые минимизируют функцию пригодности (евклидово расстояние) по отношению к каждому точка в D. В clusterP каждый агент pl ∈ P представляет собой решение с набором позиций Ol = {ol, j | j = 1, ..., k}. Алгоритм представленный на рисунке 1 показывает метод ClusterP.

Алгоритм ClouserP

Рисунок 1 – Алгоритм ClouserP

ClusterP работает следующим образом: он получает данные D и целое число k. Во-первых, он сочетается каждый агент p в среде, каждый из которых содержит набор центроидов O (строка 1). Затем,о н присваивает каждой записи di кластеру Ch, если расстояние с его центром тяжести (di, oh) равно минимальный (строки 3-8). Затем он получает когнитивную и глобальную позицию (строки 9-12), и обновляет каждую из своих скоростей и положений центроидов (строки 13-16). Алгоритм останавливается после фиксированного числа итераций или если нет значительных прогресс осуществляется в соответствии с функцией фитнеса.

6.2 Автоматическая кластеризация PSO

ClusterP был расширен в [15], чтобы автоматически найти оптимальное количество кластеров.

Новый метод называется AutoCP. Он начинается с числа k кластеров (k ≤ n), и он удаляет непоследовательные кластеры.

Форма для обнаружения несогласованных кластеров описывается следующим образом: во-первых, для каждого кластера Cj вычисляем его вес Wj = ∑| Cj |q = 1 dist (oj, dq) в виде суммы расстояний от центр oj к его точкам qj, где qj = oj. Сразу же все веса W из кластеров сортируются. Затем нормируем все веса Wj относительно кластера с наименьшим значение Ws, так что множество локальных порогов становится th = {thj | j = 1, ..., k, thj = Ws / Wj, Ws = argminw ∈ W (w)}. Наконец, кластер Cj объявляется несогласованным, если его порог t j ниже глобального порога T, тогда как T находится в диапазоне [0,1]. Алгоритм представлен на рисунке 2.

Улучшенный алгоритм ClouserP

Рисунок 2 – Улучшенный алгоритм ClouserP

Как уже упоминалось ранее, AutoCP просто добавляет механизм для ClusterP для автоматического обнаружения кластеров без дальнейшей модификации (строки 6-15). В конце каждого итерации, мы выбираем и отбрасываем несогласованные кластеры.

Выводы

Одной из наиболее сложных проблем обработки изображений является выделение контура объектов для их дальнейшего распознавания. Ключевой является задача выделения линий, проходящих на границах однородных областей.

Так как в большинстве случаев границы на изображениях выражены не столь контрастно, поэтому существующие на данный момент алгоритмы и операторы не обеспечивают эффективность получаемого результата. Часто результат обработки варьируется от разрывов контуров и линий (фрагментированность) до полного отсутствия границы. Одним из наиболее перспективных, на мой взгляд, является подход, основанный на выделении контуров на малоконтрастных и размытых изображениях на основе фрактальной фильтрации. Фракталы более наглядно выделяют контуры, чем другие операторы, но они ориентированы на обработку малоконтрастных изображений в целом, а не на выделение отдельных линий и границ.

В этой работе была описана техники разведки роя, а именно: рой частиц оптимизации. Были подробно описан алгоритм, основанный на этой парадигме. Новые алгоритмы улучшают базовый кластерный метод, который на самом деле основано на K-значении.

Список источников

  1. Gonzalez D., Woods D., Hildreth E. Theory of edge detection/Dslash Proc. R. Soc. (London). 2009. B207. 187 – 217c.
  2. Lakshmi S, Sankaranarayanan V. (2010) A Study of edge detection techniques for segmentation computing approaches, Computer Aided Soft Computing Techniques for Imaging and Biomedical Applications. - P. 35–41.
  3. Зуев А.А. Методы выделения контуров на изображениях / А.А. Зуев, Г.Е. Нечепоренко // Международная научная конференция MicroCAD: Секцiя № 8 - Мікропроцесорна техніка в автоматиці та приладобудуванні - НТУ ХПИ, 2012. - С. 108.
  4. Kennedy, J., Ebenhart, R.: Particle Swarm Optimization. In: Proceedings of the 1995 IEEE Int. Conf. on Neural Networks, pp. 1942–1948 (1995)
  5. Passino, K.: Biomimicry of bacterial foraging for distributed optimization and control. Control Systems Magazine, 52–67 (2002)
  6. Engelbrecht, A.: Fundamentals of Computational Swarm Intelligence. Wiley, Chichester (2005)
  7. Heylighen, F., Joslyn, C.: Cybernetics and second-order cybernetics. Encyclopedia of Physical Science and Technology. Academic Press, New York (2001)
  8. Bergh, F.: An analysis of particle swarm optimizers. PhD Thesis, University of Pretoria, South Africa (2002)
  9. Van der Merwe, D., Engelbrecht, A.: Data Clustering using particle swarm optimization. In: The 2003 congress on Evolutionary Computation, vol. 1, pp. 215–220 (2003)
  10. Biswas, A., Dasgupta, S.: Synergy of PSO and bacterial foraging optimization: A comprehensive study on. Advances in Soft Computing Series, pp. 255–263. Springer, Heidelberg (2007)
  11. Holdsworth B. Digital logic design / B. Holdsworth, C. Woods. – Prentice Hall, 2002. – 519 pp.
  12. Abraham, A., Roy, S.: Swarm intelligence algorithms for data clustering. Chp. 12, 279–313 (2008)
  13. Asuncion, A., Newman, D.: UCI Machine Learning Repository. University of California, Irvine, School of Information and Computer Sciences (2007)
  14. Clerc, M., Kennedy, J.: The particle swarm: Explosion, stability and convergence. IEEE Transactions on Evolutionary Computation 6, 58–73 (2002)
  15. Zhan, Z-H.; Zhang, J. Adaptive Particle Swarm Optimization. IEEE Transactions on Systems, Man, and Cybernetics. 39 (6): 1362–1381