Українська   English
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

В современном обществе широко используются технологии глобальных навигационных спутниковых систем (ГНСС).

Сегодня GPS-наблюдения является важным элементом многих геодезических работ, таких как: сгущение геодезических сетей, привязка локальной координатной системы к глобальным системам координат, кадастровые работы, привязка аэрофотосъемки, геодезический мониторинг сдвижения земной поверхности и множество других.

Наибольшая точность достигается применением дифференциальных методов измерений. Эти методы предусматривают использование как минимум комплекта из двух приёмников, один из которых устанавливается на пункт с известными координатами, а второй на определяемую точку.

1. Актуальность темы

Приёмники – это достаточно дорогостоящее оборудование, поэтому для экономии средств желательно применять методики с одним прибором. В этом случае необходимо использовать перманентные станции. В настоящий момент существует множество коммерческих компаний, которые за определённую плату предоставляют данные для обработки, например, такие как: «System Solutions», «ГЕОСПАЙДЕР», «HIVE», «EFT-CORS» и др. Такие станции находятся на открытой местности и в непрерывном режиме выполняют накопление данных для возможности совместной обработки наблюдений дифференциальными методами. При этом некоторые международные и государственные компании предоставляют данные бесплатно: «EUREF», «Главный центр контроля навигационного поля Украины». Недостатком этих сетей является редкое расположение станций по территории или же отдалённость от территории Донбасса.

2. Цель и задачи исследования

Цель данного исследования состоит в обосновании возможности применения на территории Донбасса перманентных станций, которые находятся на больших расстояниях.

Задачи исследования:

  1. Обработка данных, полученных с различных станций открытых сетей.
  2. Анализ полученных результатов для оценки сферы применения данных систем.
  3. Анализ факторов, которые могут влиять на точность получения координат.
  4. Разработка технологии и определение области применения измерений ГНСС для целей землеустройства и геодезии.

3. Обзор состояния исследований данного вопроса

Для анализа возможности применяя базовых станций, необходимо обозначить основные факторы, влияющие на точность определения координат. Анализ литературных источников [1-6] позволяет выделить основные источники ошибок:

– ошибки наблюдателя (неточное измерение высоты антенны, ошибки центрирования, ошибки в показаниях метеоаппаратуры);

– ошибки аппаратуры, к которым относятся ошибки фазовых и кодовых отсчетов, характеризующих шум аппаратуры, ошибки в измеренных временных задержках или поправках часов, как на спутнике, так и в приемнике, нестабильность фазовых центров антенн;

– влияние внешних условий по трассе распространения сигнала (неоднородности тропосферы и ионосферы, многопутность, интерференция, ослабление сигналов из-за препятствий, влияние магнитных бурь);

– ошибки математической обработки (слабая геометрия созвездия спутников, ошибки орбит и априорных координат начала базовой линии, ошибки геофизических моделей или стохастических моделей).

Навигационные сигналы, проходя от спутника к приемнику, взаимодействуют с частицами атмосферы, которые могут быть заряженными (ионосфера) и нейтральными (тропосфера). При прохождении сигналов через атмосферу меняется их скорость (рефракция). У приемников, находящихся на расстоянии 25 км, разность ионосферных вертикальных задержек может достигать 0.1–0.2 м [2]. После выполнения дифференциальной коррекции типичная остаточная погрешность для спутников вблизи зенита будет около 0.1–0.2 м при расстоянии между пунктами 100 км, но при активной ионосфере может достигать 1 м и даже больше.

Из-за того что тропосфера является недиспергирующей средой, задержки связанные с прохождением через нее невозможно устранять в двухчастотных наблюдениях, в отличие от ионосферной [2]. Показатель преломления зависит от состояния атмосферы, то есть в свою очередь от температуры воздуха, давления, влажности. Два приемника, удаленных на несколько километров, могут находиться в различных погодных условиях [2]. Поэтому для больших расстояний или при значительной разности высот нужно отдавать предпочтение раздельному введению поправок за тропосферу на базовом и роверном приемнике.

Минимизация ошибки тропосферы осуществляется с помощью специальных тропосферных моделей, которые строятся на основании некоторых средних метеорологических условий по модели стандартной атмосферы для дня года и координат (широты и долготы) пользователя.

В ряде источников описано такое воздействие тропосферы на точность получения координат. В работе [7] авторами определено что, использование модели «Saastamoinen» и модели «Hopfield» имеет тенденцию давать самые надежные результаты. Другое исследование [8] экспериментально продемонстрировало влияние различных тропосферных моделей на нигерийскую постоянную сеть GNSS.

Увеличение длины базовой линии приводит к более высокой тропосферной задержке, это наблюдается с максимальной длиной 1060,5 км. Аналогичные результаты получены в работе [9], где выполнено сравнение результатов GPS наблюдений, полученных при трех разных глобальных тропосферных моделях: «Saastamoinen», «Hopfield», «Neil». В целом установлено, что модель «Saastamoinen» позволила получить более точный результат на 89% в плане и 92% по высоте, чем модели «Hopfield» и «Neil». В работе [10] охарактеризовано влияние молекулярного и особенно нерезонансного поглощения сигналов в атмосфере. Сделан вывод, что ослабление сигналов в туманах и дождях слабо влияет на точность в дециметровом и сантиметровом диапазонах волн и практически не влияют на её значения в диапазоне метровых волн. Так же и в работе [11] установлено, что при сравнении результатов базовых линий (от 150 км до 1900 км), полученных из использования пяти различных стандартных тропосферных моделей, оптимальным вариантом была выбрана модель «Hopfield».

Так как базовые станции могут располагаться достаточно далеко от определяемых пунктов, следует отметить проблему определения таких линий. В статье [12] приведено исследование по обработке сверхдлинных базовых линий (длиной более 1 500 км). Автором определены координаты векторов из обработки, после чего выполнено сравнение измеренных базовых линий с «физическим эталоном» (роль которого выполняли пункты и каталог IGS (Международной ГНСС-службы)) и с «теоретическим эталоном» (роль которого выполняли замкнутые векторные фигуры). Приведенные эксперименты показали, что измерения и обработка сверхдлинных базовых линий с помощью коммерческого программного обеспечения дают результаты с погрешностью около 5 см.

В работе [13] выполнены измерения на расстояниях 62–154 км, были получены результаты, которые обработаны в разных программах продуктах. В эксперименте участвовали наблюдения с интервалами 1 час, 30 мин, 20 мин, 10 мин, 5 мин. Получены колебание погрешностей координат в пределах 0,0186–0,5721 м. Авторами статьи был сделан вывод, что в данных исследованиях были получены хорошие результаты при реализации сетевой обработки измерений при больших длинах базовых линий. В другом исследовании [14] рассмотрены возможности двух программных комплексов для постобработки GPS измерений. Экспериментальным путем показана достижимость геодезических уровней точности определения координат для искомых точек в сети станций при длинах базовых линий порядка 60-100 км.

При выполнении работы возникает также проблема влияния продолжительности сессий относительных статических наблюдений. В работе [15] исследовано такое влияние для двухчастотных приемников на среднюю квадратичную погрешность (СКП) длин векторов, которые предусмотрены в государственных сетях 2 класса, то есть от 5 до 20 км. Исследования показали, что реальная точность длин векторов, определенных по результатам наблюдений двухчастотными приемниками американских фирм, является существенно выше указанных в технических характеристиках приемников. При данных расстояниях и времени наблюдений от 1 до 12 часов СКП находится в пределах от 2 до 4 мм.

В работе [16] выполнено исследование для выявления влияния продолжительности сеансов наблюдений на точность плановых координат пунктов в небольших спутниковых сетях при различном количестве и расположения исходных пунктов. Сделан вывод о том, что в сети с длинами сторон до 42 км и продолжительностью сеансов 4 часа точность положения пунктов составила не менее 4 мм, а при продолжительности сеансов 2,5 ч уменьшилась на 70%. По продолжительности в 1 час – почти в 2,5 раза, то есть зависимость между точностью пунктов и продолжительности сеансов наблюдений меняется, если изменяется длина сторон в сети.

В работе [17] выполнены RTK измерения с помощью постоянно действующих станций на территории Сербии. Авторами сделан вывод о том, что точность RTK сети постоянных станций находится в пределах 2-3 см, а отклонения, превышающие эти величины, могут возникать только в случае плохой геометрии спутников, когда PDOP больше 4. Длины базовых линий находились в пределах 15-40 км. Результаты аналогичных сетей [18] показывают, что горизонтальная и вертикальная точность была 1-3 см и 5-7 см соответственно. Эти результаты получены для точек в радиусе 30 км от сети.

При обработке данных имеет место проблема выбора количества базовых станций и влияние на точность. Поэтому в статье [19] выполнено сравнение точности GPS-измерений с использованием одной или нескольких базовых станций. Использование нескольких базовых станций при кодовых измерениях подтвердило повышение точности координирования по сравнению с одиночной станцией. Использование одной базовой станции с кодово-фазовыми измерениями дало близкие результаты по сравнению с измерениями с помощью нескольких базовых станций.

4. Сбор и обработка наблюдений

В данной работе были получены необработанные файлы наблюдений из открытых сетей перманентных станций (рис. 1):

– Главный центр контроля навигационного поля Украины (ГЦКНПУ) [20].

– EUREF Permanent GNSS Network [21].

– EFT CORS [22].

Расположения перманентных станций EUREF и EFT CORS

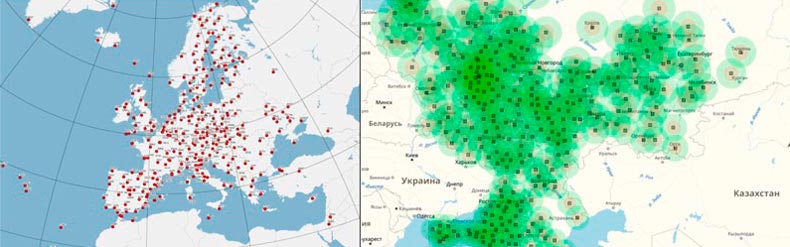
Рисунок 1 – Расположения перманентных станций EUREF и EFT CORS

Так сеть GNSS EUREF функционирует под эгидой подкомиссии Региональной справочной системы IAG (Международная ассоциация геодезии) для Европы. Она состоит из:

– сеть постоянно работающих навигационных спутниковых систем GNSS (например, GPS, GLONASS, Galileo, Beidou);

– центры обработки данных, обеспечивающие доступ к данным станции;

– аналитические центры, которые регулярно анализируют данные GNSS;

– центры продуктов или координаторы;

– центральное бюро, которое отвечает за ежедневный мониторинг и управление.

Центр контроля навигационного поля (ЦКНП) вместе с сетью контрольно-корректирующих станций (ККС) составляют основную измерительную сеть «Системы координатно-временного и навигационного обеспечения Украины» (СКНОУ). ЦКНП СКНОУ предназначен для мониторинга целостности глобальной навигационной спутниковой системы (ГНСС), формирование дифференциальной коррекционной информации (ДКИ), что обеспечивает на территории Украины повышение точности нахождения местоположения пользователя согласно сигналам ГНСС.

Сеть базовых станций GNSS-станций EFT-CORS – инфраструктурный проект группы компаний EFT GROUP. Сервис EFT-CORS подразумевает создание сплошного навигационного поля поправок RTK и необработанных данных для постобработки на территории Российской Федерации. Подключаясь к данному сервису, пользователь получает круглосуточный доступ к любой из базовых станций действующей сети без ограничения по времени работы. Данные для постобработки предоставляются бесплатно всем желающим, прошедшим регистрацию и активацию на ресурсе.

Из каждой сети выбраны наиболее приближенные станции к Донецку (рис. 2). Расстояния от перманентных станций до Донецка составляют от 100 до 240 км.

Схема расположения перманентных станций

Рисунок 2 – Схема расположения перманентных станций (анимация: 8 кадров, 10 циклов повторения, 134 КБ)

При выборе данных для выполнения исследования соблюдались такие требования:

– на каждой из станции должны быть наблюдения в один и тот же период;

– различная длительность накопления информация (от 0,5 до 2 часов);

– выбор дней наблюдений в разные периоды года.

Непосредственно обработка будет выполняться в программном продукте «Topcon Tools». Данное программное обеспечение предназначено для обработки и уравнивания наблюдений, полученных различными геодезическими приборами.

Все файлы наблюдений конвертируются в RINEX, который является общепринятым форматом обмена данными для файлов исходных данных спутниковых навигационных приёмников. Также стоить отметить, что обработку можно выполнять при трех доступных в программе тропосферных моделях: «Niell», «UNBabc», «Goad and Goodman».

После получения результатов, для оценки точности необходимо определить среднеквадратические ошибки по формуле [23]:

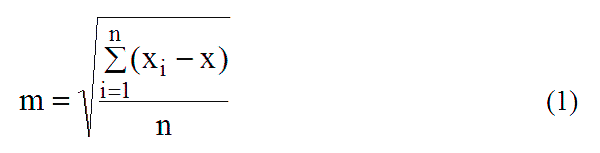
Среднеквадратическая ошибка

где

xi – значения координат полученные после обработки, м;

x – эталонные значения координат, м;

n – количество измерений.

За эталонные значения приняты точные координаты, которые предоставлены в открытом доступе.

5. Анализ результатов измерений

В соответствии с ранее определенными источниками ошибок определим возможные факторы, которые могут повлиять на точность определения координат:

– метеорологические параметры (давление, влажность, температура);

– PDOP (снижение точности по местоположению, характеризующие геометрическое взаиморасположение спутников относительно антенны приёмника);

– длительности наблюдений на станциях;

– количество наблюдаемых спутников;

– длина базовой линии.

Одним из методов определения зависимости данных факторов от полученных погрешностей является регрессия.

5.1 Множественная регрессия

Множественная регрессия применяется для исследования явлений, которые определяются большим числом одновременно и совокупно действующих факторов. В связи с этим возникает задача исследования зависимости одной зависимой переменной Y от нескольких объясняющих переменных X1, X2...Xn. Эта задача решается с помощью множественного регрессионного анализа [24].

Общий вид записи регрессионной модели с несколькими объясняющими переменными:

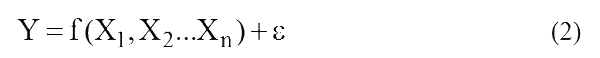
Общий вид записи регрессионной модели

Линейная регрессионная модель с несколькими объясняющими переменными (Классическая линейная модель множественной регрессии (КЛММР)), имеет уравнение вида:

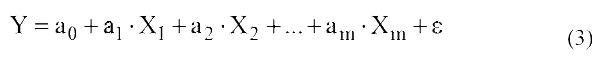
Линейная регрессионная модель

где

Y – зависимая, объясняемая, результирующая, эндогенная переменная (показатель);

Xm – переменные (или признаки), характеризующие результат или эффективность функционирования анализируемой экономической системы;

ε – регрессионные остатки (случайное возмущение) или стохастическая переменная, отражающая влияние неучтенных в модели и неизвестных факторов;

am – параметры линейного уравнения множественной регрессии.

5.2 Оценка параметров линейного уравнения множественной регрессии

Для нахождения коэффициентов регрессионной зависимости (3) используется метод наименьших квадратов (МНК). МНК для оценки параметров линейной множественной регрессии приводит к построению и решению соответствующей системы нормальных уравнений [25]:

Метод наименьших квадратов

Для удобства представим данные наблюдений и параметры модели в матричной форме:

n-мерный вектор-столбец наблюдений

где

Y – n-мерный вектор-столбец наблюдений зависимой переменной.

Матрица значений независимых переменных

где

X – прямоугольная матрица значений независимых (факторных) переменных размерности.

Вектор-столбец параметров уравнения регрессии

где:

A – m-мерный вектор-столбец параметров уравнения регрессии.

В этих обозначениях эмпирическое уравнение регрессии выглядит так:

Эмпирическое уравнение регрессии

В результате преобразований получаем выражение для вектора параметров регрессии:

Вектоа параметров регрессии

Пользуясь методом наименьших квадратов, необходимо помнить о том, что он дает BLUE – оценки коэффициентов регрессии (Best Linear Unbiased Estimater), только при выполнении следующих условий:

– Регрессионная модель линейна относительно коэффициентов аj (j=1,2,...m), случайного члена ε.

– Случайный член имеет нулевое математическое ожидание.

– Случайные члены в различных наблюдениях не коррелированы друг с другом (no serial correlation).

– Случайный член имеет постоянную дисперсию (no heteroskedasticity).

– Ни одна из объясняющих переменных не является линейной комбинацией других объясняющих переменных (no perfect multicollinearity).

– Случайный член имеет нормальный закон распределения.

5.3 Множественная корреляция

Показатели множественной корреляции характеризуют тесноту (силу) связи рассматриваемого набора факторов с результативным признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

К показателям множественной корреляции относятся:

– Множественный коэффициент корреляции;

– Корреляционное отношение;

– Индекс корреляции.

Множественный коэффициент корреляции вычисляется по формуле:

Множественный коэффициент корреляции

При этом коэффициентом множественной детерминации R2 называется квадрат множественного коэффициента корреляции [26]. Коэффициент множественной детерминации характеризует, на сколько процентов построенная модель регрессии объясняет вариацию значений результативной переменной относительно своего среднего уровня, т. е. показывает долю общей дисперсии результативной переменной, объяснённой вариацией факторных переменных, включённых в модель регрессии.

5.4 Анализ вариации зависимых переменных в регрессии

Оценка значимости построенного уравнения регрессии в целом производится с помощью F – критерия Фишера.

Оценить значимость уравнения регрессии – означает, что необходимо установить, соответствует ли регрессионная модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания результативной переменной [25].

Оценку статистической значимости включения фактора в уравнении регрессии (последовательно), оценивают с помощью частных F–критериев по следующей формуле:

Множественный коэффициент корреляции

Оценка значимости коэффициентов чистой регрессии осуществляется с помощью критерия Стьюдента:

Критерий Стьюдента

Расчетные критерии Стьюдента сравнивают с критическим (табличным) значением t-критерия при определенном уровне значимости и числе степеней свободы. При этом если расчетный критерий больше табличного, то нулевую гипотезу о несущественности (статистической незначимости, недостоверности) коэффициента регрессии при заданном уровне значимости можно отклонить.

Выводы

По изученной литературе можно сделать вывод о том, что не существует полномасштабного исследования применения перманентных станций при больших расстояниях до определяемых пунктов, которые были бы актуальны для условий Донбасса.

Поэтому в процессе данного исследования предполагается обосновать возможность применения существующих перманентных станций глобальной навигационной сети для целей землеустройства и геодезии в условиях Донбасса. С помощью определенных СКП возможно будет установить сферу применения данных сетей и технологию использования.

При этом такое исследование позволит сократить затраты на выполнение спутниковых наблюдений. Это будет достигаться за счет: использования бесплатных ресурсов, применения только одного приемника и уменьшения количества работников выполняющих измерения.

Также для оценки возможных погрешностей будет проведен анализ факторов, которые влияют на точность координат. Такой анализ даст возможность определить значимые факторы и степень их влияния на результат. Что позволит прогнозировать и выбирать оптимальные базовые станции, периоды и длительность наблюдений.

Список источников

  1. Антонович К. М.; Использование СРНС в геодезии. Том 1 / Антонович К. М., – Москва: ФГУП Картгеоцентр, 2005 – 334 с.
  2. Антонович К. М.; Использование СРНС в геодезии. Том 2 / Антонович К. М., – Москва: ФГУП Картгеоцентр, 2005 – 360 с.
  3. Физические принципы работы GPS/ГЛОНАСС [Текст]: монография / А. К. Синякин, А. В. Кошелев. – Новосибирск: СГГА, 2009. – 110 с.
  4. On Ground-Based GPS Tropospheric Delay Estimation /Schuler T., – Munich: University of the Bundeswehr, 2001. – 364 p.
  5. Бахвалов В. Б. Основні джерела помилок GPS-спостережень / В. Б. Бахвалов, В. В. Вишнівський, Р. М. Леоненко // Збірник наукових праць Військового інституту Київського національного університету імені Тараса Шевченка / Військовий інститут. – Київ, 2010., т. 25, pp. 378-381.
  6. Генике А. А., Побединский Г. Г. Глобальные спутниковые системы определения местоположения и их применение в геодезии. Изд. 2-е, перераб. и доп. -М.: Картгеоцентр, 2004. – 355 с.
  7. C. Satirapod and P. Chalermwattanachai, «Impact of different tropospheric models on GPS baseline accuracy: Case study in Thailand,» Journal of Global Positioning Systems, vol. 4, no. 1-2, pp. 36-40, 2005.
  8. Joseph D. Dodo, Tahir A. Yakubu, Lazarus M. Ojigi and Samuel Y. Tsebeje Determination of the best-fit Tropospheric Delay Model on the Nigerian // FIG Working Week 2013, Environment for Sustainability. – Abuja, Nigeria: 6 – 10 May 2013.
  9. Dodo, Joe D. and Kamarudin, Mohd. The influence of different global tropospheric models on baseline precision in a local GPS network: Case of the Malaysian Johor RTKnet. // Exhibition on Geoinformation and International Symposium and Exhibition on Gps/Gnss. – Persada Johor INternational Convention Centre, Johor Bahru, Johor.: 5-7 November 2007.
  10. Р. П. Быстров, А. В. Соколов, Л. В. Федорова. Статистика дальности РЛС в гидрометеорах // М.: Журнал радиоэлектроники № 7. – 2012 – с. 19-21.
  11. Hamed M., Shaker A., Saad A., Mahmoud S. The Effect of Different Tropospheric Models and Ocean Tide on long Baselines // Conference: National Recearch Institute of Astronomy and Geophysic. – Egypt: 2010.
  12. А. А. Струков. Анализ точности определения векторов сверхдлинных базовых линий по результатам GPS-измерений.// ВЕСТНИК СГГА. – 2011. – Выпуск 2 (15). – С. 30-38.
  13. Горб А., Нежальский Р., Федоренко Р. Анализ точности программного обеспечения постобработки GPS-измерений в сети перманентных станций // Авиационно-космическая техника и технология.-2005.,-№ 3.-с. 70-76.
  14. Горб А. И, Федоренко Р. Н., Нежальский Р. В. Анализ программного обеспечения постобработки GPS-измерений в сети перманентных станций // Авиационно-космическая техника и технология.-2005.-с. 70-76..
  15. SКостецька Я. До питання точності довжин векторів, отриманих за результатами відносних GPS–спостережень двочастотними приймачами / Я. Костецька, Ю. Пішко // Сучасні досягнення геодезичної науки та виробництва:, збірник наукових праць Західного геодезичного товариства УТГК – Львів: Видавництво Національного університету «Львівська політехніка», 2009. – Випуск 1 (17). – С. 92–97.
  16. Костецька Я. Залежність точності визначення положення пунктів у супутникових мережах від тривалості сеансів спостережень / Я. Костецька, Ю. Пішко, Д. Гешель // Сучасні досягнення геодезичної науки та виробництва: збірник наукових праць Західного, геодезичного товариства УТГК /. – Львів: Видавництво Львівської політехніки, 2011. – Випуск 2 (22). – С. 96-102.
  17. Delcev Sinisa, Ogrizovic Vukan , Vasilic Violeta, Gucevic Jelena Accuracy Testing of RTK Service of the Permanent Station Network in the Republic of Serbia // FIG Working Week 2009, Surveyors Key Role in Accelerated Development . – Eilat, Israel: 3-8 May 2009.
  18. Rudolf W. Present Status of the Indonesian Permanent GPS Station Network and Development Matindas // Congress & Session: 7th FIG Regional Conference. – Subarya, Cecep : 2009.
  19. Асташенков Г. Г., Мазуров Б. Т., Зарзура Ф. Х. Влияние количества базовых станций на точность ГНСС-измерений // Известия высших учебных заведений. Геодезия и аэрофотосъемка / Из-во: Московский государственный университет геодезии и картографии "., – Москва, 2013 – № 3. – с. 62-63.
  20. Центр контролю навігаційного поля України. [Електронний ресурс] – Режим доступу до ресурсу: http://gcknp. com. ua.
  21. EUREF Permanent GNSS Network [Электронный ресурс] – Режим доступа: http://www. epncb. oma. be.
  22. Сервис EFT CORS [Электронной ресурс] – Режим доступа: http://eft-cors. ru.
  23. Большаков В. Д. Теория ошибок наблюдений: Учебник для вузов – 2-е изд., перераб. и дол. M., Недра, 1983. 223 с.
  24. Эконометрика: учебник для магистров / И. И. Елисеева и др.]; под ред. И. И. Елисеевой. – М.: Издательство Юрайт, 2014. – 453 с.
  25. Эконометрика: учебник/ Ю. В. Сажин, И. А. Иванова; Мордов. гос. ун-т. – Саранск, 2014. – 316 с.
  26. Эконометрика: конспект лекций / А. М. Варюхин, О. П. Панкина, А. В. Яковлева. – Москва: Юрайт, 2007. – 191 с.