Abstract
Content
- Introduction
- 1. Relevance of the topic
- 2. The purpose and objectives of the study
- 3. Review of the status of research on this issue
- 4. Collection and processing of observations
- 5. Analysis of measurement results
- Conclusion
- References
Introduction
Global navigation satellite systems (GNSS) technologies are widely used in modern society.
Today, GPS observations are an important element of many geodetic works, such as: thickening geodetic networks, linking the local coordinate system to global coordinate systems, cadastral works, linking aerial photography, geodetic monitoring of the earth surface displacement and many others.
The greatest accuracy is achieved using differential measurement methods. These methods involve the use of at least a set of two receivers, one of which is set at a point with known coordinates, and the second at a point to be determined.
1. Relevance of the topic
Receivers – it is quite expensive equipment, so to save money, it is desirable to apply the techniques with a single device. In this case it is necessary to use permanent stations. At the moment there are many commercial companies that provide data for processing for a certain fee, for example, such as: System Solutions, GEOSPIDER, HIVE, EFT-CORS, etc. Such stations are located in open areas and in the continuous mode, accumulation of data is performed in order to enable joint processing of observations by differential methods. However, some international and state-owned companies provide data for free: “EUREF”, “Main Center for Control of the Navigation Field of Ukraine”. The disadvantage of these networks is the rare location of stations on the territory or remoteness from the territory of Donbass.
2. The purpose and objectives of the study
ЦThe purpose of this study is to substantiate the possibility of using permanent stations on the territory of Donbass, which are located at large distances.
Objectives of the study:
- Processing of data received from various stations of open networks.
- Analysis of the results to assess the scope of these systems.
- Analysis of factors that may affect the accuracy of obtaining coordinates.
- РDevelopment of technology and determination of the scope of GNSS measurements for land management and geodesy.
3. Review of the status of research on this issue.
To analyze the possibility of applying base stations, it is necessary to identify the main factors affecting the accuracy of determining the coordinates. Analysis of literary sources [1-6] пallows to identify the main sources of errors:
– errors of the observer (inaccurate measurement of the antenna height, errors of centering, errors in the readings of the meteorological equipment);
– - errors of the equipment, which include errors of phase and code samples, characterizing the noise of the equipment, errors in the measured time delays or clock corrections, both on the satellite and in the receiver, instability of the phase centers of the antennas;
– the influence of external conditions on the signal propagation path (inhomogeneities of the troposphere and ionosphere, multipath, interference, weakening of signals due to obstacles, the effect of magnetic storms);
– errors of mathematical processing (weak geometry of the constellation of satellites, errors of orbits and a priori coordinates of the baseline origin, errors of geophysical models or stochastic models).
Navigating signals, passing from the satellite to the receiver, interact with particles of the atmosphere that can be charged (ionosphere) and neutral (troposphere). When passing signals through the atmosphere, their speed (refraction) changes. For receivers located at a distance of 25 km, the difference in ionospheric vertical delays can reach 0.1–0.2 m [2]. After performing a differential correction, the typical residual error for satellites near the zenith will be about 0.1–0.2 m with a distance between points of 100 km, but with an active ionosphere it can reach 1 m and even more.
The tropospheric error is minimized using special tropospheric models, which are based on some average meteorological conditions using the standard atmosphere model for the day of the year and the coordinates (latitude and longitude) of the user.
A number of sources described the effect of the troposphere on the accuracy of obtaining coordinates. In [7], the authors determined that the use of the Saastamoinen model and the Hopfield model tends to give the most reliable results. Another study [8] experimentally demonstrated the effect of various tropospheric models on the Nigerian permanent GNSS network.
An increase in the length of the baseline leads to a higher tropospheric delay; this is observed with a maximum length of 1060.5 km. Similar results were obtained in [9], where the results of GPS observations obtained with three different global tropospheric models were compared: “Saastamoinen”, “Hopfield”, “Neil”. In general, it was found that the Saastamoinen model allowed for a more accurate result of 89% in terms of and 92% in height than the Hopfield and Neil models. The influence of molecular and especially nonresonant absorption of signals in the atmosphere was characterized in [10]. СIt is concluded that attenuation of signals in fogs and rains has little effect on accuracy in the decimeter and centimeter wavelengths and practically does not affect its values in the range of meter waves. It was also found in [11] that when comparing the results of baselines (from 150 km to 1900 km) obtained from the use of five different standard tropospheric models, the optimal choice was the “Hopfield” model.
Since base stations can be located quite far from the designated points, it should be noted the problem of identifying such lines. The article [12] presents a study on the processing of super-long baselines (over 1 500 km long). The author determined the coordinates of the vectors from the processing, after which the measured baselines were compared with the “physical standard” (which was played by the IGS (International GNSS-Service) catalog) and with the “theoretical standard” (the role of which were performed by closed vector shapes). Experiments have shown that measuring and processing super-long baselines using commercial software give results with an error of about 5 cm.
In [13] measurements were made at distances of 62–154 km, and results were obtained that were processed in different programs of products. The experiment involved observations at intervals of 1 hour, 30 minutes, 20 minutes, 10 minutes, 5 minutes. Oscillations of coordinate errors within 0.0186–0.5721 m were obtained. The authors of the article concluded that good results were obtained in these studies when implementing network processing of measurements with large baseline lengths. In another study [14], the capabilities of two software systems for post-processing GPS measurements were considered. The experimentally shown reachability of geodetic levels of accuracy in determining the coordinates for the desired points in the network of stations with baseline lengths of the order of 60-100 km.
When performing work, there is also the problem of the influence of the duration of the sessions of relative static observations. In [15], such an effect was studied for dual-frequency receivers on the mean square error (MSE) of vector lengths, which are provided for in public networks of class 2, that is, from 5 to 20 km. Studies have shown that the real accuracy of the lengths of the vectors determined from the results of observations by two-frequency receivers of American firms is significantly higher than those indicated in the technical characteristics of the receivers. With these distances and observations from 1 to 12 hours, the EUC is in the range from 2 to 4 mm.
When processing data, there is the problem of choosing the number of base stations and the effect on accuracy. Therefore, the article [16] compared the accuracy of GPS measurements using one or several base stations. The use of several base stations in code measurements confirmed the improved coordination accuracy compared to a single station. Using one base station with code-phase measurements yielded similar results as compared to measurements using several base stations.
4. Collection and processing of observations
In this work, we received the raw observation files from the open networks of permanent stations (Fig. 1):
– The main center of control of the navigation field of Ukraine [17].
– EUREF Permanent GNSS Network [18].
– EFT CORS [19].
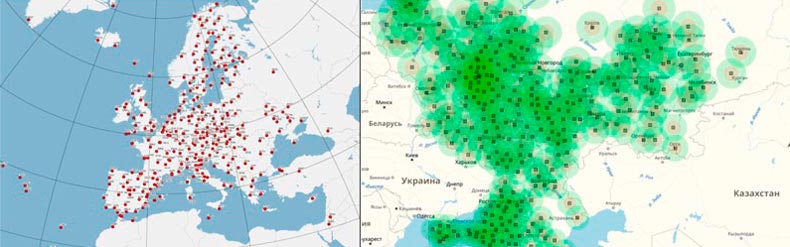
Figure 1 – Location of permanent stations EUREF and EFT CORS
So the GNSS EUREF network operates under the auspices of the subcommittee of the IAG (International Association of Geodesy) Regional Reference System for Europe. It consists of:
– network of constantly operating navigation satellite systems GNSS (for example, GPS, GLONASS, Galileo, Beidou);
– data centers providing access to station data;
– think tanks that regularly analyze GNSS data;
– product centers or coordinators;
– central office, which is responsible for daily monitoring and management.
The center of control of the navigation field (CCNP), together with the network of control and correction stations (CCS), constitute the main measuring network “Systems of coordinate-time and navigation support of Ukraine” (SKNOU). CCNP SKNOU is designed to monitor the integrity of the global navigation satellite system (GNSS), the formation of the differential correction information (DKI), which provides in Ukraine an increase in the accuracy of finding the user’s location according to the GNSS signals.
The network of base stations of GNSS stations EFT-CORS is an infrastructure project of the EFT GROUP group of companies. The EFT-CORS service implies the creation of a continuous navigation field for the RTK amendments and raw data for post-processing in the territory of the Russian Federation. By connecting to this service, the user gets round-the-clock access to any of the base stations of the existing network with no time limit. Data for post-processing is provided free of charge to everyone who has been registered and activated on the resource.
From each network, the closest stations to Donetsk were selected (Fig. 2). Distances from permanent stations to Donetsk range from 100 to 240 km.

Figure 2 – The layout of permanent stations (animation: 8 frames, 10 cycles of repetition, 134 KB)
When selecting data to perform the study the following requirements were met:
– each station must have observations in the same period;;
– different accumulation duration information (from 0.5 to 2 hours);
– choice of days of observations in different periods of the year.
НDirect processing will be performed in the software product “Topcon Tools”. This software is designed to process and equalize observations made by various geodetic instruments.
ВAll observation files are converted into RINEX, which is a common data exchange format for source data files of satellite navigation receivers. It is also worth noting that processing can be performed with three tropospheric models available in the program: “Niell”, “UNBabc”, “Goad and Goodman”.
After obtaining the results, to estimate the accuracy, it is necessary to determine the root-mean-square errors using the formula [20]:
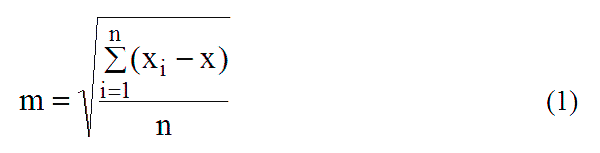
where
xi – coordinate values obtained after processing, m;
x – reference values of coordinates, m;
n – number of measurements.
For reference values taken the exact coordinates that are provided in the public domain.
5. Analysis of measurement results
In accordance with the previously identified sources of error, we determine possible factors that may affect the accuracy of determining the coordinates:
– meteorological parameters (pressure, humidity, temperature);
– PDOP (decrease in accuracy by location, characterizing the geometric position of the satellites relative to the receiver antenna);
– duration of observations at stations;
– number of satellites observed;
– baseline length.
One of the methods for determining the dependence of these factors on the errors obtained is regression.
Multiple regression is used to study phenomena that are determined by a large number of simultaneously and collectively acting factors. In this connection, the problem arises of studying the dependence of one dependent variable Y on several explanatory variables X1, X2...Xn. This problem is solved using multiple regression analysis [21].
General view of the regression model record with several explanatory variables:
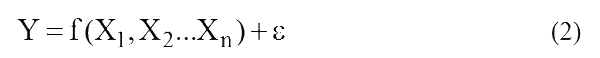
A linear regression model with several explanatory variables (the Classic linear multiple regression model) has an equation of the form:
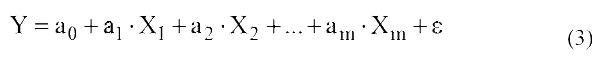
where:
Y – dependent, explainable, resulting, endogenous variable (indicator);
Xm – пvariables (or signs) characterizing the result or efficiency of functioning of the analyzed economic system;
ε – regression residuals (random perturbation) or a stochastic variable, reflecting the effect of unrecorded and unknown factors in the model;
am – parameters of the linear equation of multiple regression.
Conclusion
From the literature studied, it can be concluded that there is no full-scale study of the use of permanent stations at large distances to designated points that are relevant to the conditions of Donbass.
Therefore, in the course of this study, it is supposed to substantiate the possibility of using the existing permanent stations of the global navigation network for land management and geodesy in the Donbass environment. With the help of certain MSE, it will be possible to establish the scope of application of these networks and technology of use.
In this case, such a study will reduce the cost of satellite observations. This will be achieved by: using free resources, using only one receiver and reducing the number of workers performing measurements.
Also, to assess possible errors, an analysis will be made of factors that affect the accuracy of coordinates. Such an analysis will make it possible to determine the significant factors and the degree of their influence on the result. That will allow to predict and select the optimal base stations, periods and duration of observations.
References
- Антонович К. М.; Использование СРНС в геодезии. Том 1 / Антонович К. М., – Москва: ФГУП Картгеоцентр, 2005 – 334 с.
- Антонович К. М.; Использование СРНС в геодезии. Том 2 / Антонович К. М., – Москва: ФГУП Картгеоцентр, 2005 – 360 с.
- Физические принципы работы GPS/ГЛОНАСС [Текст]: монография / А. К. Синякин, А. В. Кошелев. – Новосибирск: СГГА, 2009. – 110 с.
- On Ground-Based GPS Tropospheric Delay Estimation /Schuler T., – Munich: University of the Bundeswehr, 2001. – 364 p.
- Бахвалов В. Б. Основні джерела помилок GPS-спостережень / В. Б. Бахвалов, В. В. Вишнівський, Р. М. Леоненко // Збірник наукових праць Військового інституту Київського національного університету імені Тараса Шевченка / Військовий інститут. – Київ, 2010., т. 25, pp. 378-381.
- Генике А. А., Побединский Г. Г. Глобальные спутниковые системы определения местоположения и их применение в геодезии. Изд. 2-е, перераб. и доп. -М.: Картгеоцентр, 2004. – 355 с.
- C. Satirapod and P. Chalermwattanachai, “Impact of different tropospheric models on GPS baseline accuracy: Case study in Thailand,” Journal of Global Positioning Systems, vol. 4, no. 1-2, pp. 36-40, 2005.
- Joseph D. Dodo, Tahir A. Yakubu, Lazarus M. Ojigi and Samuel Y. Tsebeje Determination of the best-fit Tropospheric Delay Model on the Nigerian // FIG Working Week 2013, Environment for Sustainability. – Abuja, Nigeria: 6 – 10 May 2013.
- Dodo, Joe D. and Kamarudin, Mohd. The influence of different global tropospheric models on baseline precision in a local GPS network: Case of the Malaysian Johor RTKnet. // Exhibition on Geoinformation and International Symposium and Exhibition on Gps/Gnss. – Persada Johor INternational Convention Centre, Johor Bahru, Johor.: 5-7 November 2007.
- Р. П. Быстров, А. В. Соколов, Л. В. Федорова. Статистика дальности РЛС в гидрометеорах // М.: Журнал радиоэлектроники № 7. – 2012 – с. 19-21.
- Hamed M., Shaker A., Saad A., Mahmoud S. The Effect of Different Tropospheric Models and Ocean Tide on long Baselines // Conference: National Recearch Institute of Astronomy and Geophysic. – Egypt: 2010.
- А. А. Струков. Анализ точности определения векторов сверхдлинных базовых линий по результатам GPS-измерений.// ВЕСТНИК СГГА. – 2011. – Выпуск 2 (15). – С. 30-38.
- Горб А., Нежальский Р., Федоренко Р. Анализ точности программного обеспечения постобработки GPS-измерений в сети перманентных станций // Авиационно-космическая техника и технология.-2005.,-№ 3.-с. 70-76.
- Горб А. И, Федоренко Р. Н., Нежальский Р. В. Анализ программного обеспечения постобработки GPS-измерений в сети перманентных станций // Авиационно-космическая техника и технология.-2005.-с. 70-76..
- SКостецька Я. До питання точності довжин векторів, отриманих за результатами відносних GPS–спостережень двочастотними приймачами / Я. Костецька, Ю. Пішко // Сучасні досягнення геодезичної науки та виробництва:, збірник наукових праць Західного геодезичного товариства УТГК – Львів: Видавництво Національного університету “Львівська політехніка”, 2009. – Випуск 1 (17). – С. 92–97.
- Асташенков Г. Г., Мазуров Б. Т., Зарзура Ф. Х. Влияние количества базовых станций на точность ГНСС-измерений // Известия высших учебных заведений. Геодезия и аэрофотосъемка / Из-во: Московский государственный университет геодезии и картографии "., – Москва, 2013 – № 3. – с. 62-63.
- Центр контролю навігаційного поля України. [Електронний ресурс] – Режим доступу до ресурсу: http://gcknp. com. ua.
- EUREF Permanent GNSS Network [Электронный ресурс] – Режим доступа: http://www. epncb. oma. be.
- Сервис EFT CORS [Электронной ресурс] – Режим доступа: http://eft-cors. ru.
- Большаков В. Д. Теория ошибок наблюдений: Учебник для вузов – 2-е изд., перераб. и дол. M., Недра, 1983. 223 с.
- Эконометрика: учебник для магистров / И. И. Елисеева и др.]; под ред. И. И. Елисеевой. – М.: Издательство Юрайт, 2014. – 453 с.
