Реферат за темою магістерської роботи
Зміст
- Вступ
- 1. Мета роботи
- 2. Сутність метода
- 3. Критерії для оцінки знака коренів характеристичного рівняння
- 4. Програмне забезпечення для оцінки статичної стійкості
- 5. Оцінка знака коренів за допомогою алгебраїчних критеріїв
- 6. Приклад дослідження СС регульованої системи АРВ пропорційного типу
- Висновки
- Перелік літератури
Вступ
Статична стійкість (СС), або стійкість сталого режиму, — це здатність електричної системи повертатися до вихідного становища після малого його збурення (відхилення режимних параметрів) [1].
У будь-якій електричній системі встановлений режим не означає постійність всіх його параметрів. Електрична система має велику кількість навантажень, які змінюються, причому ці змінення появляються та зникають. У зв`язку з чим на генераторах системи з`являються деякі додаткові незначні моменти, також стохастическі, які зменшують або збільшують моменти, які діють на валах генераторів й зсовуючи їх ротори на невеликі кути [6].
Таким чином, в електричній системі постійно відбуваються малі збурення, причина яких та місто виникнення не фіксовані. Ці деякі вільні збурення, які визивають вільний рух, котрий може бути зростаючим або затухаючим, коливальним або аперіодичним. Його характер визначає статичну стійкість, яка є необхідною умовою працездатності системи. Статична стійкість перевіряється при перспективному й робочому проектуванні, розробці спеціальних пристроїв автоматичного регулювання (розрахунки та експерименти), введенні до експлуатації нових елементів системи, зміненні умов експлуатації [7].
Дослідження статичної стійкості приводяться в плані рішення задач аналізу або синтезу.
При рішенні задач аналізу перевіряється стійкість режиму, який встановився, визначається гранично стійкий режим електричної системи, заданої усіма параметрами, оцінюються деякі показники якості перехідного процесу.
При рішенні задач синтезу визначається тип системи збудження й його регулювання, закон регулювання, параметри системи збудження й регуляторів. При цьому виходять із заданих вимог до гранично стійкого режиму або якості електроенергії у встановленому режимі.
Задача визначення умов статичної стійкості і характеру перехідних процесів дуже велика, особливо, для реальних складних систем, які мають автоматичні регулятори збудження та швидкості. Для полегшення розв’язання цієї задачі застосовують різні математичні прийоми та методи. Одним з найрозповсюджених методів дослідження статичної стійкості є метод малих коливань із застосуванням спеціальних критеріїв, які оцінюють знаки дійсних коренів, або дійсних частин комплексно-сполучених коренів характеристичних рівнянь, і таким чином, визначають характер перехідного процесу (ПП).
1. Мета роботи
Метою магістерської роботи є розробка програмного забезпечення для дослідження СС електричних систем різної складності методом малих коливань за допомогою практичних алгебраїчних та частотних критеріїв на ПЕОМ.
Для досягнення поставленої мети будуть вирішуватись такі задачі:
- аналіз теоретичних положень дослідження статичної стійкості електричних систем за допомогою алгебраїчних критеріїв (Гурвіца, Рауса) і частотних критеріїв (Михайлова, D-розбиття);
- розробка програмного забезпечення для реалізації цих методів на ПЕОМ;
- розробка методичних вказівок для дослідження статичної стійкості з використанням ПЗ.
2. Сутність метода
Збурення в системі, які визивають малі відхилення, розглянуті при дослідженні статичної стійкості, не визначаються не за місцем їх виникнення, не за величиною. Тобто, походження збурення таке, що встановити абсолютні значення параметрів режиму при їх відхиленнях від встановлених (початкових) значеннях неможливо. Таким чином, задача дослідження статичної стійкості зводиться до задачі визначення тільки характеру змінення параметрів режиму.
При встановленні практичних критеріїв відповідь була тільки у формі так-ні
, стійкий-нестійкий
режим від начального його стану при малих збуреннях. Встановити який в будь-якому випадку буде характер перехідного процесу (аперіодичний, коливальний, затухаючий, зростаючий) можливо вирішив або проаналізував систему нелінійних диференційних рівнянь.
Російським математиком Ляпуновим А.М. було доказано, що судити статичну стійкість можливо по лінеаризованій системі рівнянь, оскільки малі відхилення — це такі, при яких система поводиться як лінійна. Ним були доведені дві теореми сутність яких полягає в методі першого приближення (перший метод Ляпунова): система стійка в малому (статично), якщо стійке її лінійне приближення.
Метод вивчення статичної стійкості за лінеаризованими рівняннями отримав назву метода малих коливань або малих відхилень [4]. Лінеаризація складається в слідуючому. Будь-яку незалежну змінну і зображують як суму постійної величини у вихідному режимі й нескінченно малого приближення:

Розклавши нелінійні функції в ряд Тейлора та залишивши тільки лінійні члени цього ряду, отримують систему лінійних диференційних рівнянь, але вже відносно нескінченно малих прирощень. Рішення такої системи має вид [9], [4]:

де р – корені характеристичного рівняння, яке в канонічному виді виглядає так:
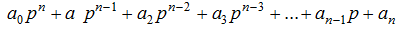
Кількість складових дорівнює порядку системи рівнянь. Так як коефіцієнти характеристичного рівняння, які визначаються реальними параметрами системи, дійсні числа, то його корені можуть бути або дійсними, або комплексно-сопряженими. Таким чином, склавши характеристичне рівняння та визначив його корені, можливо визначити характер змінення малих прирощень параметрів режиму у часі. Дійсному кореню відповідає член виду  . Парі комплексно-сопряжених коренів
. Парі комплексно-сопряжених коренів 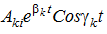 . Коли всі корені й дійсні частини всіх комплексних коренів від`ємні, то всі складові перехідного процесу за модулем експоненціально затухають. Розглядаємий режим в цьому випадку статично стійкий. Коли серед дійсних коренів з`являється хоча б один додатний, то відповідна складова перехідного процесу буде експоненціально необмежено зростати. Вихідний режим статично нестійкий (аперіодичне порушення стійкості або
. Коли всі корені й дійсні частини всіх комплексних коренів від`ємні, то всі складові перехідного процесу за модулем експоненціально затухають. Розглядаємий режим в цьому випадку статично стійкий. Коли серед дійсних коренів з`являється хоча б один додатний, то відповідна складова перехідного процесу буде експоненціально необмежено зростати. Вихідний режим статично нестійкий (аперіодичне порушення стійкості або сповзання
). Коли серед комплексних коренів з`явиться пара, маюча додатну частину, то відповідна складова буде мати вигляд наростаючих у часі коливань.
Таким чином, необхідною та достатньою умовою статичної стійкості вихідного режиму електричної системи являється вимога від`ємності всіх дійсних коренів та дійсних частин всіх комплексних коренів характеристичного рівняння. Існують методи (критерії), які дозволяють визначати знаки коренів і таким чином судити про стійкість системи не визначаючи самих коренів характеристичного рівняння. Порядок операцій для дослідження статичної стійкості електричних систем методом малих коливань складається в наступному [9]:
- Складається математичний опис перехідних процесів в системі у вигляді нелінійних диференційних рівнянь.
- Проводиться лінеарізація вихідних рівнянь з метою одержання лінеаризованих рівнянь.
- Складається характеристичне рівняння та характеристичний детермінант.
- Оцінюється стійкість за допомогою критеріїв, які виявляють знаки коренів.
3. Критерії для оцінки знака коренів характеристичного рівняння
Критерії стійкості класифікують як прямі, які потребують знаходження коренів, та непрямі, які не потребують розрахунків самих коренів. До них відносять алгебраїчні (метод Гурвіца, Рауса) й частотні (метод Михайлова, Найквіста, D-розбиття).
4. Програмне забезпечення для оцінки статичної стійкості
Програма створюється в середовищі математичного інтегрованого пакету Mathcad. Це пояснюється тим що, інтегрований пакет має можливість об`єднання фрагментів різних систем між собою, одночасно використовуючи убудовані Windows можливості. До них відносять:
- використання всіх інструментів Windows;
- сучасний багато віконний інтерфейс;
- кольорове оформлення документів;
- створення анімаційних динамічних файлів;
- створення звукового супроводу.
Ці системи мають зручний інтерфейс — сукупність засобів спілкування з користувачем у вигляді вікон, які переміщуються, клавіш та інших елементів. Вони мають ефективні засоби наукової графіки. Враховуючи, що більша частина часу потребується на підготовку тексту, доцільно працювати в середовищі текстового редактора Word, а об’єкти вставляти із MathCAD [3]. Така вставка в текстовий процесор об’єктів із математичної системи MathCAD дає повноцінний доступ до всіх можливостей і засобам останньої. Можливо також з використанням гіперпосилань визивати файл, створений в середовищі MathCAD. За допомогою спеціальний клавіш при використанні гіперпосилань легко здійснюють повертання до попереднього або наступного документу. Текст, формули і прості рисунки (вихідні схеми, схеми заміщення) формуються безпосередньо в редакторі Word. Ілюстрації, які представляють собою графічний результат розрахунків (векторні діаграми, функціональні залежності та інші) формуються в середовищі MathCAD з наступним впровадженням отриманого рисунка в документ Word. Анімаційні рисунки (обертові векторні діаграми і координатні осі, функції і графіки, а також послідовність результатів рішення для різних вихідних даних та інш.) також створюються в середовищі MathCAD. Для створення послідовності кадрів анімації використовується стандартна технологія створення анімаційних файлів з розширенням avi
. Подвійний натиск лівої клавіші миші при установці курсору на рисунок, який виконано засобами системи MathCAD дозволяє активізувати останню та використати її можливості для аналізу, вплив різних факторів на характер протікання перехідного процесу. Якщо закрити вікно MathCAD, здійсниться повертання до документу Word, який вивчався. Анімаційні рисунки можуть викликатися безпосередньо із документу Word за допомогою гіперпосилань, або тимчасово створюватися в середовищі MathCAD. Виконання різного роду розрахунків можливо робити, якщо визвати із текстового файлу, на підставі існуючих посилань, документи MathCAD та навпаки при виконанні розрахунків можливо звертатися до текстового матеріалу для отримання необхідної допомоги. Це дозволяє виключити дублювання матеріалу, котрий, звичайно, поміщується в методичні вказівки для виконання практичних занять.
Програмне забезпечення (ПЗ) розробляється для найпростішої електричної системи, яка наведена на рис.1

Рисунок 1 – Схема найпростішої електричної системи
(анімація складається з 8 кадрів з затримкою 500 мс між кадрами, кількість циклів відтворення – 3, розмір – 10 кілобайт)
5. Оцінка знака коренів за допомогою алгебраїчних критеріїв
Критерій Гурвіца.
Для регульованої системи з АРЗ пропорційного типу значення коефіцієнтів характеристичного рівняння [4], [9]:
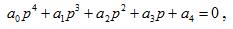
де

Розраховується детермінант Гурвіца, всі додаткові визначники та корені характеристичного рівняння. На екран монітора виводяться для вихідних даних значення згаданих визначників Гурвіца. Розраховуються корені характеристичного рівняння системи, яка досліджується за допомогою засобів символьної математики Mathcad [3]:
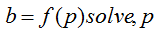
Виконується зіставлення значень всіх визначників Гурвіца і отриманих коренів характеристичного рівняння. На підставі цього зіставлення робляться висновки про умови порушення СС різних видів (аперіодичного, періодичного і самозбудження). Аналіз дозволяє визначити умови порушення стійкості при різних значеннях коефіцієнту підсилення АРЗ. Можливо також виявлення впливу на значення ku постійної часу регулювання. Розраховується також детермінант Гурвіца, всі додаткові визначники та корені характеристичного рівняння. Виконується аналіз всіх цих параметрів та робляться висновки про умови порушення статичної стійкості.
Критерій Рауса
Для найпростішої регульованої системи з АРЗ пропорційного типу розраховуємо коефіцієнти строк таблиці. Елементи кожної наступної строки знайдемо за формулою [5], [10]:

где k – номер стовбця; i – номер строки, в якій знаходиться коефіцієнт. На екран виводиться складена таблиця Рауса. На підставі кількості змінення знака в першому стовпці робляться висновки про умови порушення СС різних типів.
6. Приклад дослідження СС регульованої системи АРВ пропорційного тип
Для того, щоб система працювала статично стійко при великих кутах за 90, необхідно вводити регулювання збудження [8], 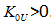 Відомо, що статично стійко система працюватиме при виконанні наступної умови.
Відомо, що статично стійко система працюватиме при виконанні наступної умови.

де
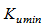 – мінімально необхідний коефіцієнт підсилення;
– мінімально необхідний коефіцієнт підсилення;
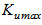 – максимально припустимий коефіцієнт підсилення [2]. Зміна згаданих коефіцієнтів залежно від вихідного кута навантаження наведені на рис.2
– максимально припустимий коефіцієнт підсилення [2]. Зміна згаданих коефіцієнтів залежно від вихідного кута навантаження наведені на рис.2
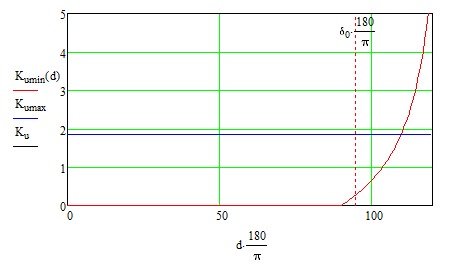
Рисунок 2 - Зміна коєффіціентов посилення в залежності від вихідного кута навантаження.
Анімація (кількість кадрів:5, кількість циків:5, об'єм: 5,79 кБ)
ля заданих параметрів системи, яка досліджується значення максимально допустимого коефіцієнта не залежить від вихідного кута і становить 1,855. Мінімально необхідний коефіцієнт залежить від вихідного режиму. Бачимо, що система може працювати статично стійко при введенні певного коефіцієнта посилення.
При  в системі буде відбуватися порушення стійкості апериодичного типу. За умови
в системі буде відбуватися порушення стійкості апериодичного типу. За умови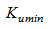 типу саморозгойдування.
типу саморозгойдування.
Розглянемо приклад коли система стійка
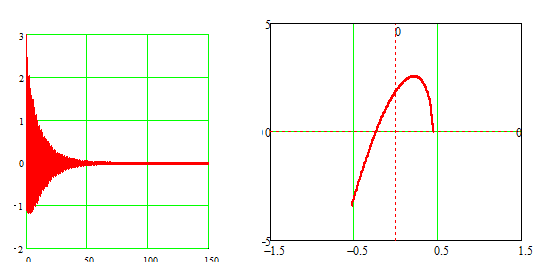
Рисунок 3 - Характер перехідного процесу і годограф Михайлова
З аналізу наведених рис.3 видно, що при заданих вихідних параметрах режиму коливальний процес носить затухаючий характер, що відповідає стійкій системі. Годограф Михайлова при цьому також відповідає стійкій системі.
Висновки
Таким чином розробка програмного забезпечення для оцінки статичної стійкості регульованих електричних систем, визначення знаків дійсних коренів, або дійсних частин комплексних коренів характеристичних рівнянь, графічна інтерпретація за допомогою Mathcad, дає ряд переваг: наочність, простота, можливість визначення стійкості, не вдаючись до додаткових розрахунками.
На момент написання реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2014 Після зазначеної дати повний текст роботи та матеріали по темі можуть бути отримані у керівника.
Перелік літератури
- Статическая устойчивость [Электронный ресурс]. – Режим доступа: http://dic.academic.ru.
- Жданов П. С. статическая устойчивость сложныхэлектрических систем. – М.: 1940,
- Дьяконов В. П. : Mathcad 11/12/13 в математике. – Москва
Высшая школа
2007. – С. 315-530. - Переходные электромеханические процессы в электрических системах: Учеб. для электроэнергет. спец. вузов. – 2 – е изд, перераб. и доп. Венников В. А. / М.: Высш. шк, 1970. – 472 с,
- Методы расчета устойчивости энергосиcтем [Электронный ресурс]. – Режим доступа: http://portal.tpu.ru.
- Нелинейная коррекция сильного регулирования возбуждения генераторов. Кощеев Л. А., Невельский В. Л. –
Труды НИИПТ
, 1977, вып. 26. - Ульянов С. А. Электромагнитные переходные процессы. – М.: Энергия, 1970, 518с,
- Статическая устойчивость электрических систем с синхронными машинами, снабженными автоматическими регуляторами возбуждения: Лекции / Розанов М. Н. – М. 1959,
- Переходные электромеханические процессы в электрических системах: Учеб. для электроэнергет. спец. вузов. – 4-е изд., перераб. и доп. Венников В. А. / М.: Высш. шк., 1985. – 536 с.,
- Рюденберг Р., Переходные процессы в электрических системах, изд-во иностранной литературы, 1955.
