УДК 004.942
МОДЕЛИРОВАНИЕ СИСТЕМ УРАВНЕНИЙ ДИНАМИКИ ДВИЖЕНИЯ ТРАНСПОРТНОГО СРЕДСТВА НА ПАРАЛЛЕЛЬНОЙ АРХИТЕКТУРЕ
Аннотация
Хайдуков А. В., Кривошеев С. В., Штепа В. Н. Моделирование систем уравнений динамики движения транспортного средства на параллельной архитектуре. Выполнен анализ уравнений для расчета параметров движения транспортных средств – судов внутреннего плавания. Определен оптимальный метод решения системы дифференциальных уравнений. Обосновано использование параллельной архитектуры на базе графического процессора для решения поставленной задачи. Приведены результаты работы программы для расчета параметров транспортного средства с использованием параллельной архитектуры.
Annotation
Khaidukov A. V., Krivosheev S. V., Shtepa V. N. Modeling of the system of equations of the dynamics of motion of a vehicle on a parallel architecture. The analysis of the equations for the computing of the parameters of the movement of vehicles – inland navigation vessels – is done. An optimal method for solving a system of differential equations is determined. The use of a parallel architecture based on a graphics processor to solve the problem is substantiated. The results of a program for calculating vehicle parameters using a parallel architecture is shown.
Введение
Важную роль в современном мире играет обеспечение безопасности движения транспортных средств, снижении субъективного фактора и повышения надежности управления [1]. Автоматизация систем управления движением как транспортного средства в целом, так и совокупностью участников движения позволяет увеличить безопасность движущихся объектов транспортного потока, более интенсивно эксплуатировать транспортный коридор, снизить затраты топлива, а также оптимально использовать режим работы двигателя транспортного средства. В связи с этим растет потребность в использовании интегрированных навигационных систем для вычисления безопасного и оптимального пути.
Целью данного исследования является разработка программного обеспечения для моделирования систем уравнений динамики движения судна. Расчет параметров должен производиться с использованием средств параллельных вычислений.
Математическая модель динамики движения транспортного средства
Одной из математических моделей для вычислений и расчета параметров движения является модель с тремя степенями свободы, которая рассматривает движение судна в двумерном пространстве (рис. 1) [2]. Данная модель необходима, чтобы рассчитывать проекции скорости и координаты местонахождения объекта.
Перевод скорости из подвижной системы координат Oxyz в неподвижную Orhn выполняется с помощью матрицы пересчета:

где vX и vY – проекции вектора скорости судна на оси X и Y соответственно в подвижной системе координат, ψ – курс судна.
![Рисунок 1 – Неподвижная система координат Orhn [3]](images/article1_pic2.png)
Рисунок 1 – Неподвижная система координат Orhn [3]
В результате вывода физических формул и множественных математических преобразований получаем систему уравнений для вычисления необходимых параметров движения судна:

где m – масса судна;
vvX и vY – скорость судна по оси X и Y соответственно;
ω – угловая скорость судна;
L – длина судна;
JZ – момент инерции массы судна;
lR – расстояние от центра судна до движительно-рулевого комплекса (ДРК);
ZP – число ДРК;
XA, YA, MA – продольная, боковая силы и момент аэродинамических сил, действующих на надводную часть судна;
TRi и YRi – полезная тяга и боковая сила i-го ДРК;
k11, k22 – присоединенные массы судна при движении по осям X и Y соответственно;
k66 – присоединенный момент инерции судна;
k26 – присоединенный статический момент;
R – сопротивление воды;
YK – боковая гидродинамическая сила неинерционной природы;
MK – момент гидродинамических сил относительно вертикальной оси, проходящей через центр судна [4].
Для системы уравнений (2) формулируется задача Коши (3).
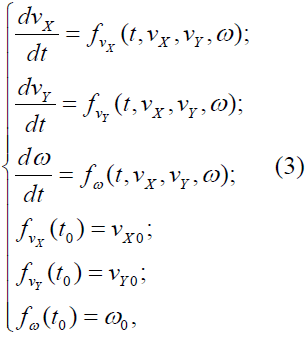
где t0 – начальное время исследования движения судна;
vX0, vY0 – скорость движения судна по оси X и Y соответственно в начальный момент времени t0;
ω0 – угловая скорость судна в t0 [4].
Предварительно система уравнений (2) преобразуется к виду, удобному для применения численных методов. Если известны величины vX, vY и ω в начальный момент времени t0, то возможно найти значение данных параметров судна в последующие моменты времени. Для решения сформулированной задачи Коши используется численный метод Рунге-Кутты четвертого порядка.
Таким образом, из-за высокой плотности трафика и уменьшения количества вычислительных устройств должны применяться параллельные методы вычисления, которые позволят уменьшить время расчета и увеличить количество участников движения.
Реализация вычислений с помощью параллельных архитектур
В настоящее время создается множество программ, которые обрабатывают большой объем информации. Несколько независимых частей алгоритма обработки (то есть результат выполнения одной части не влияет на результат выполнения другой) можно выполнять параллельно. Параллельные программы работают быстрее последовательных, за счет выполнения задачи на нескольких ядрах процессора. Ядро – это часть процессора, которая выполняет один поток команд. Программу можно написать, используя какую-либо параллельную библиотеку. Выбор библиотеки может зависеть от платформы, на которой программа будет выполняться, от требуемого уровня производительности и от природы самой задачи [5].
Решать задачи параллельного вычисления можно с помощью многоядерного центрального процессора (CPU). Такой процессор имеет два или более вычислительных ядра на одном кристалле. Ядро может выполнять один или несколько потоков команд. Многоядерные процессоры способы выполнять несколько потоков команд параллельно независимо друг от друга. Такой процессор относится к классу MIMD архитектур (Multiple Instruction stream Multiple Data stream – множество потоков команд, множество потоков данных). Одна из возможных архитектур двухъядерного процессора представлена на рис. 2. Разница для других многоядерных процессоров будет заключаться в количестве имеющихся ядер, а также использовании кэш-памяти, которая может быть общей или распределенной для ядер.
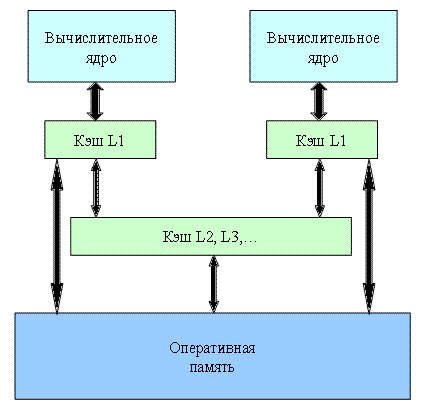
Рисунок 2 – Архитектура двухъядерного микропроцессора
Из рисунка видно, что архитектура имеет следующие особенности:
– L1 – кэш-память первого уровня, она распределена и является локальной для каждого ядра;
– кэш-память второго – L2, третьего – L3 и последующих уровней, а также оперативная память является общей для всех ядер процессора.
Основным недостатком данной архитектуры является то, что лишь одно ядро может работать с кэш-памятью второго уровня во время текущего такта.
Одним из самых распространенных способов параллельного вычисления является использование графического процессора (GPU). Большую часть GPU занимают вычислительные модули. В отличие от CPU, большую часть которого занимает кэш-память и память с произвольным доступом (RAM). Поэтому целесообразнее использовать архитектуру графического процессора, изначально предполагающую работу с одинаковыми типами данных, которые можно обрабатывать параллельно.
В данной работе для решения поставленной задачи используется программно-аппаратная архитектура параллельных вычислений CUDA.
В результате была разработана программа, позволяющая формировать рекомендуемую траекторию движения судна. Пример траектории представлен на рис. 3.
Программа использует технологию CUDA для параллельного расчета траектории движения судна. Данная технология позволяет существенно увеличить вычислительную производительность благодаря использованию графических процессоров фирмы NVIDIA.
Рисунок 3 – Траектория движения судна
С помощью такого набора средств разработки можно реализовывать алгоритмы на упрощенном диалекте языка программирования C, а также вставлять специальные функции в текст написанной программы. Такие алгоритмы могут выполняться на любых процессорах фирмы NVIDIA, поддерживающих технологию CUDA.
Выводы
В результате проведенных исследований была выбрана математическая модель для расчета параметров движения судна и метод ее решения. Выполнен обзор параллельных архитектур, в результате которого была выбрана необходимая архитектура.
Разработано программное обеспечение для расчета параметров движения судна.
Литература
1. Анучин О.Н., Емельянцев Г.И. Интегрированные системы ориентации и навигации для морских подвижных объектов. СПб.: Электроприбор, 2003. – 390 с.
2. Аноприенко А.Я., Кривошеев С.В. Разработка подсистемы моделирования движения судна по заданной траектории // Научные труды Донецкого национального технического университета. Выпуск 12. Серия «Вычислительная техника и автоматизация». – Донецк, ДонГТУ, ООО «Лебедь», 1999. С. 197-202.
3. Снопков В.И. Управление судном. СПб.: Профессионал, 2004 – 536 с.
4. Ходкость и управляемость судов. Под ред. В.Г. Павленко. М.: Транспорт, 1991. – 396 с.
5. Классификация архитектур по параллельной обработке данных [Электронный ресурс]. – Режим доступа: http://www.csa.ru/analitik/distant/q_4.html