UA   RU
DonNTU   Masters' portal

Analysis and implementation of the configuration interaction model for fullerenes

Content

Introduction

The problem of correct accounting of interaction between electrons arose already in the first years after the creation of quantum mechanics [1 – 3] when it was discovered close relationship with electron spin degree of freedom [4]. Moreover, from two electronic versions of it, which explained the nature of the covalent chemical bond [5], to applications of mathematical permutation group apparatus [6, 7], unitary formalism [8 – 10] and up to its subgroups of spatial symmetry [11] the complexity of computational circuits grew exponentially. Cluster approaches [12], opening up the possibility of attracting chemical intuition, also do not solve the problem of effectively correct accounting of multiplicity of the state and its symmetry, including spatial, to study the properties of complex molecular systems.

A finite state machine model proposed by E. Moore in 1956 and named in his honor (Moore machine) as a synchronous sequential circuit, is part of many digital systems and is used in the construction of control devices. High complexity integrated circuits (which continue to increase, following the law of G. Moore) and the theoretical basis of automatic calculations makes possible the implementation of complex information processing algorithms. However, the direct implementation of algorithms can lead to inefficient use of crystal resources and increase the cost of the project.

1. Relevance of the topic

The discovery of a truncated icosahedron carbon cluster [13] and then tubular hydrocarbons [14] in 60 and 70s first was a brilliant foresight, not a contradiction for theoretical chemistry. But then, in the 80s and 90s, experimentally [15, 16] new carbon compounds, fullerenes and nanotubes were discovered. The expected discoveries of these high spatial carbon compounds symmetry, including the icosahedron symmetry, turned out to be revolutionary and gave a new direction in nano–technologies. They are used in many areas including medicine. This makes the problem of effective theoretical study of their unexpected, interesting for applications relevant properties of such nano structures.

Nano objects are interesting, first of all, for their supramolecular properties: the dynamics of ions, atoms and guest molecules, as well as the ability to send and receive electrons in mild conditions. In particular, they are associated with the basic biological functions of protein bodies (electron and proton transport, the vast majority of catalytic biochemical reactions). It is also characteristic of carbon nanostructures that they can act both as reducing agents and as weak oxidizing agents. In turn, such properties are determined by the electronic structure of objects, which has both common features and unconditional and striking differences. The quantum–chemical approach to their study allows us to consider these two, at first glance, very different classes of compounds (see Figure 1), fullerenes and nanotubes, as cluster objects of carbon atoms, only of different spatial symmetries.

In fullerene, pentagons form 30o positive curvature of the plane of the hexagons (dome), and heptagons can give 30o negative curvature of the plane (the inside of the donut, if form it from a nanotube). Such distortions can cause semiconductor conductivity.

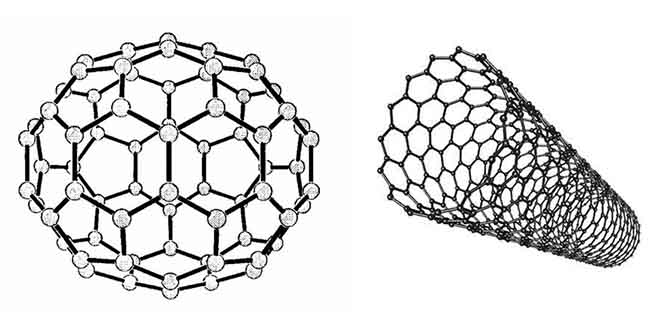
Модель молекулы фуллерена C60 и углеродной нанотрубки

Figure 1 – The model of the fullerene C60 molecule and the carbon nanotube

The lowest fullerene C20 is a regular dodecahedron consisting of 12 pentagons, the structure of the remaining fullerenes necessarily contains 12 pentagons and a certain number of hexagons (in C60 there are 20) (see Figure 1). Since a feature of a carbon atom is its ability to form almost any complex volumetric structure consisting of polygons, carbon nanostructures, due to their size, actually serve as a bridge between individual molecules and crystals.

The electrical, optical and mechanical properties of fullerenes in a condensed state indicate a rich physical content of phenomena occurring with the participation of fullerenes. Crystalline fullerenes and films from them are semiconductors with a band gap of 1.2–1.9 eV and have photoconductivity under optical irradiation. Fullerenes in crystals are characterized by relatively low binding energies; therefore, phase transitions are observed in them even at room temperature, leading to orientational disordering and unfreezing of the rotation of fullerene molecules. C60 crystals doped with alkali metal atoms have metallic conductivity and pass into the superconducting state in the range from 19 to 55 K, depending on the type of alkali metal.

Many people attribute the discovery of fullerenes to a possible revolution in organic chemistry. Fullerene molecules in which carbon atoms are linked by both single and double bonds are three–dimensional analogues of aromatic structures, for example, C48 [17]. Possessing high electronegativity, they act in chemical reactions as sufficiently strong oxidizing agents. By adding radicals of various chemical nature to themselves, fullerenes are capable of forming a wide class of chemical compounds possessing its endohedral complexes already synthesized in macro amounts. In the latter, one or more atoms of metals, non–metals, or even individual molecules are placed inside the carbon sphere. Based on such complexes, it is expected that highly effective anti–cancer drugs will be created in the future.

The explanation of such unique physical and chemical properties of fullerenes lies, of course, in the peculiarities of their electronic and atomic structure. So, if in classical flat aromatic structures s – and p – bonds are geometrically orthogonal, then in fullerenes and nanotubes, due to the non–zero curvature of their surfaces, there are not.

The addition of radicals containing platinum group metals to C60 makes it possible to obtain fullerene–based ferromagnetic material. Compounds, the structure of which is obtained by replacing part of the carbon atoms with metals, reveal new chemical properties. Such compounds called metal carbonates include, for example, Ti8C12, V8C12, Hf8C12, Zr8C12. It is worth noting that fullerene C28 [19] also has magnetic properties.

The variety of physicochemical and structural properties of compounds based on fullerenes allows us to speak about the chemistry of fullerenes as a new promising area of organic chemistry. Its development can lead to unpredictable results [16, 18].

2. Goal and tasks of the research

Goals of research are:

  1. Combining different methods of a self–consistent field, from one configuration to many configuration interactions, taking into account spatial symmetry, for example, fullerenes and nanotubes, when calculating their electronic, magnetic and optical properties in a single approach of the Fock coordinate function and density matrix.
  2. Description of the application of the properties of unitary, orthogonal, and spatial symmetry groups to highlight all possible states of the open shell of a highly symmetric system containing up to five degenerate orbitals of an irreducible representation, for example, an icosahedron group, for which it is possible to calculate the constants in the energy functional and in the variational equations corresponding to each of its conditions, and give a way to its implementation.
  3. A review of the achievements, in the same unified approach, of advances in solving the question of the applicability of molecular methods for the calculation of atoms with open shells.
  4. Creation of a single software product that combines the methods applicable for calculating the electronic states of fullerenes, nanotubes and fullerites with an open shell.
  5. Studying the nature of convergence of the iterative process for solving equations that give optimization of molecular orbitals and a minimum of state energy, and studying methods that give guaranteed convergence of the process of solving these equations, as well as accelerating the process of self–consistency.

3. Scientific novelty

3.1 Objects of study

In the 90s, methods for the synthesis of fullerenes in macro amounts [20] were developed and methods for their separation and purification were found [21, 22]. In addition, the most important structural and physicochemical characteristics of C60 were determined (Figure 1), the most common representative of this class of substances. To date, more than 10,000 works on fullerenes have been published, including a number of reviews [23 – 21]. The research carried out covered such seemingly distant fields of science as astronomy and organic chemistry, solid state physics and medical biology, inorganic chemistry and geometry. Fullerenes are simultaneously attributed to inorganic materials – like new allotropic modifications of carbon – and to organic compounds, since in chemical transformations they exhibit many properties of unsaturated hydrocarbons.

Currently, fullerenes have become the subject of intensive research by a large number of scientific groups, the results of which are closely monitored by applied companies (in the West, such large as Exxon, Du Pont, AT&T from the USA, NEC from Japan, Hoechst AG from Germany and other). In 1993, the journal Fullerene Science and Technology began to be published, devoted to fullerenes and bearing the word technology (its publishers included future Nobel laureates, Robert F. Curl, Harold W. Kroto, Richard E. Smolley [30]).

Fullerenes, as they turned out, are connected with the history of the development of the Earth and the solar system.

Fullerenes are part of the earth's crust, they became known after their discovery. Although, their content is small and they are distributed very unevenly; therefore, chemical studies of terrestrial fullerenes can hardly be considered complete today. Natural fullerenes are found in some minerals. The ratio of C60:C70 in them varies in the range of 0.21–0.36 [31]. It is believed that fullerenes contribute to the migration and concentration of a number of elements, in particular, they influence the formation of diamond deposits and are a catalyst for their synthesis.

How and when did fullerenes form in the earth? There is no clear understanding of this yet, especially since the ways of their formation can be very different. L. Becker and his colleagues studied the isotopic composition of inert gases captured by fullerenes during their formation and preserved inside a strong carbon shell. Samples of natural rocks with fullerenes C60 – C200 were taken from different points of our planet: they were found by geologists in Japan, China and Hungary. European samples turned out to be of little interest, while Asian ones contained a relatively high concentration of fullerenes. According to Becker [32], some fullerenes were filled – there were helium atoms inside the shells. This revealed oddities – the fullerenes did not store helium–4 – an isotope that is usually present in terrestrial rocks – but a rare helium–3 isotope for the Earth. Becker previously found fullerenes at the sites of the meteorite’s impact in Sandbury (Ontario, Canada) and the Allende asteroid in Mexico about 30 years ago. The latter is 4.6 billion years old.

The discovery made it possible to establish that such fullerenes could form only in space conditions in the so–called carbon stars or in their surroundings. Becker explained [32] that the unusually high temperatures and pressures in these stars may provide the only way by which cosmic noble gases can invade the fullerenes. This, presumably, is about the explosion of a star that occurred long before the appearance of the solar system.

It was possible to determine the time of appearance of the studied fullerenes on Earth. The crater from the fall of the Canadian meteorite was formed 1.85 billion years ago, in the Archean era, when the Earth was still lifeless, formless and empty. Other fullerenes appeared much later. Since they were discovered at the boundary of the Permian and Triassic sediments, their age is estimated at 250 million years. It was then that a formidable space guest crashed into the Earth, which wandered in its orbits for a long time – a giant asteroid or comet nucleus, which caused catastrophic destruction. This disaster is supposed to be more terrible than the asteroid impact that occurred 65 million years ago, on the border of the Cretaceous and Tertiary periods. As a keepsake, the asteroid sprayed the fullerenes and iridium that it brought [33].

It is mostly accepted that schungite rocks are the richest in fullerenes. Huge shungite deposits have so far been discovered only in one place – in Karelia, near the village of Shunga. It was in the Karelian shungites that earthly fullerenes were first discovered. One of the former Soviet scientists studied at the University of Arizona (USA) schungite samples taken from the Russian Geological Institute, and, to the surprise of the entire scientific community, discovered carbon globules with fullerenes there. After a sensational report about this, an intensive search began for other rocks containing fullerenes, questions arose about their origin on Earth.

Now, with the presence of fullerenes in shungites, some enthusiasts associate the healing effect of the marcial waters discovered in 1714, with which Peter the Great was treated. There are suggestions that some organic radicals are attached to the fullerene molecules in shungites, which allow the fullerenes to form aqueous solutions with a concentration of up to 30–50 mg / l. Though, more thorough studies have shown that some shungite deposits do contain fullerenes, while others contain only soot substances.

4. Overview of existing and evolving methods

4.1. Restricted Hartree–Fock Method

This method is described as the open shell method in [34]. It is an obvious generalization of the self–consistent field method used to calculate the ground states of atoms and molecules. As a wave function, one determinant is used, in which q orbitals are occupied by two electrons with α and β spins, whereas ρ – q orbitals are occupied by one electron with α spin i.e.:

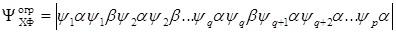
Формула 1

Equations can be found similar to the Hartree–Fock ones, from which the orbitals Формула 2 are then determined to minimize the energy corresponding to Формула 3. These equations were first derived by Lennard–Jones. They are more complicated than the usual Hartree–Fock equations, since they cannot simply be reduced to the form of eigenvalue problems. However, McVini and Rutan have developed methods for solving these equations [35]. For orbitals in the non–orthogonal basis of the Gaussian or Slater type, they can be written as resembling a generalized eigenvalue problem, although they are not a standard eigenvalue problem, since they are nonlinear:

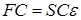
Формула 4

where F is the Fock matrix (which depends on the coefficients C due to electronic interactions), C is the matrix of coefficients, S is the matrix of overlapping basis functions, epsilon; – energy of orbitals. In the case of an orthonormal basis, the overlap matrix, S, is reduced to the identity matrix. These equations are essentially a special case of the Galerkin method.

4.2 Unrestricted Hartree–Fock Method

The restricted Hartree–Fock Method cannot be used for systems with open shells: radicals (one unpaired electron), triplet and singlet excited states of molecules (two unpaired electrons), many organic and inorganic complexes of transition metals (several unpaired electrons, populating degenerate d– or f–orbitals), isolated atoms with unfilled shells. The method of finding the wave function, similar to the RHF method, in which the spatial parts of single–electron spin orbitals vary independently, is called the unrestricted Hartree–Fock method (RHF) [36].

The obtained expressions for the Fock operator and energy are similar to the expressions of the bounded HF method, however, the Hartir–Fock–Rutan equations decompose into two interconnected systems of equations corresponding to electrons with opposite spins:

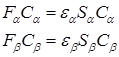
Формула 5

The self–consistency procedure remains similar to the UHF method, however, the obtained solutions have features that distinguish them from RHF ones.

  1. The coefficients of the MO of electrons with different spins Сijα and Сijβ are not the same.
  2. When the numbers of electrons with opposite spins are not equal, the energies of the spin orbitals also turn out to be different εα and εβ.

The main advantage of the UHF method is the ability to describe systems with unpaired electrons and its simplicity, since the calculation algorithm, as well as the program structure, are similar to the RHF method. Currently, the vast majority of quantum–chemical programs include modules that allow finding solutions using the UHF method.

4.3 Restricted Open–shell Hartree–Fock Method

The drawbacks of the NHF method noted above can partially be solved with the help of the Restricted Open–shell Hartree–Fock Method (ROHF), in which closed and open shells are described differently. Closed shells consist of double occupied orbitals; their splitting is not supposed. But depending on the nature of the open shell, its wave function can be one determinant, as in the case of the doublet or high–spin components of the triplet (Sz = 1 or Sz = -1), or it can be a linear combination of two or more determinants.

In the ROHF scheme, different open shells are described according to a single scheme based on a fairly general expression for energy containing numerical coefficients whose values differ for different states. In all cases, it is assumed that we are dealing with a certain N value of orthonormal (spatial) orbitals, φi, each of which can be associated with its own filling value ωi, and the electronic energy can be described as:

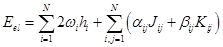
Формула 6

where the coupling coefficients, αij and βij are determined by the type of state with an open shell (i.e., for each type of open shell – a doublet, a triplet etc., the corresponding constants α and β) are selected. When these coefficients depend on the orbital number of the open shell, the terms are called non–Rutanian [40], and if they are independent of the orbital number, they are Rutanian [41].

To determine the WF, the usual procedure can be used for varying electron energy using the method of Lagrange multipliers, then the Euler equations are obtained as a result of the variation. The system of these equations breaks down into a set of N equations, the so–called k–dependent Fock operators of the ROHF, for each orbital or for each class of orbitals has its own Fock operator:

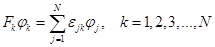
Формула 7

It is often more convenient to write down a system of equations as a single equation. To do this, a unified coupling operator is introduced, which combines all the equations, and the equations obtained then turn out to be identical to the Hartree–Fock equations and are solved in a similar way by self–consistency. Mostly, such associations are obtained using the density matrix method [39].

  1. In general, the ROHF method gives a more correct description of the WF of open systems than the RHF method, since its WF initially has the correct spin symmetry. The exception is the phenomenon of spin polarization, which was discussed in the previous section.
  2. This method demonstrates the greatest advantage in describing degenerate and high–spin systems for which NHP and other methods, with the exception of CV and MK SSP, are unsuitable and give non–symmetrical solutions.
  3. The disadvantages of this method are the need for manual setting of the coefficients ωi, αij, βij for various types of degenerate states, and also the fact that most of the programs used use single linking operators that do not reproduce the Coopmans theorem. An original method for calculating such coefficients for all Rutanian terms in a similar approach was proposed in [41].
  4. The accuracy of estimating many molecular properties in the case of low–spin and non–degenerate open–shell systems (radicals, non–degenerate triplets), as well as closed–shell systems cannot compete with the accuracy of more complex (and bulky) methods: MPn, DFT, CCSD, and QCISD.

4.4 Method of density matrix and Fock coordinate function

The Institute of Physical – Organic Chemistry and Coal Chemistry of the National Academy of Sciences of Ukraine (Donetsk) studied the properties of the density matrix [38]. The problems of spinless quantum mechanics were also solved by constructing both the Fock coordinate functions and the spatial components of the density matrix for the states of a multi–electron system with a definite full spin [42, 43] using the symmetric group [6]. The density matrix method was also used to write the Hartree–Fock–Rutan equations in a form convenient both for studying the properties of the method, including questions of its instability [39], and for studying the properties of molecules. Using the bases of the unitary and orthogonal groups Формула 8, a universal method for calculating constant coefficients in the Hartree–Fock–Rutan equations [40, 41], which are used, for instance, in calculating the Rutanian terms of fullerenes with an open shell [19, 44]. Note in more detail the theoretical foundations for the methods used.

V.A. Fock in [45, 46] wrote down the wave function ΨsM with spin s and its projection M:

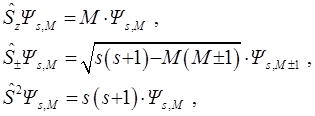
Формула 9

in the form containing the explicit separation of the spatial coordinate function Фs or the function Формула 10 with a signed factor. The last convenient in application of the Fock method:

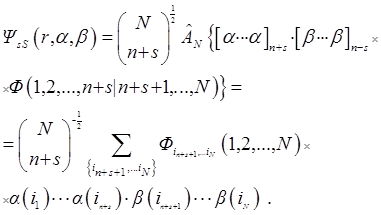
Формула 11

As in [40, 41], the coordinates of the particles are indicated by their numbers, Formula 12 – antisymmetrizator, spin functions α and β orthonormal and Формула 13Формула 14.

Identities guarantee three Fock conditions for Фs [45]. This is it's antisymmetry:

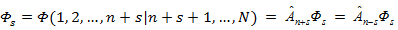
Формула 15

in each set of variables separated by a bar, and the condition of cyclic symmetry prohibiting antisymmetrization of Фs by n + s + 1st particles,

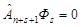
Формула 16

The line in the Fock function Фs cannot be shifted to the right. Its shift to the left gives the coordinate functions ФsM = Ф (1, 2, ..., n + M | n + M + 1, ..., N) of the ΨsM states. A shift of the line to the left by more than 2s coordinates is again prohibited by the condition of cyclic symmetry of the Fock function [34].

The Fock coordinate function can be constructed for various approximate methods: from the Hartree – Fock – Rutan method [41] to the coordinate function of the full configuration interaction method in [47].

A convenient algorithm for their application is based on the common for all coupling approximations of the densities of the Fock Fock coordinate functions Фs = Ф (1, 2, ..., n + s | n + s + 1, ..., N) of the corresponding partiality calculated for each approximation separately:

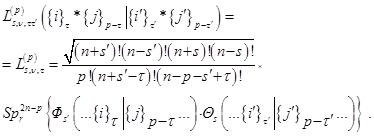
Формула 17
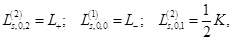
Формула 18

with single–particle applications: charge, Формула 19, and spin ds densities:

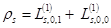Формула 20;
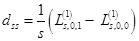Формула 21,

and with two–particle, – spatial, R, spin–orbit, D, and spin–spin, F, densities:

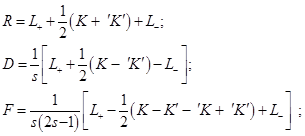
Формула 22

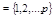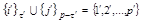Here ν = s′ - s = τ - τ′, and the spatial non–hatched and hatched coordinates of the particles, standing before and after the stroke in the functions Формула 23 and Формула 24, indicated by their numbers: Формула 25 Формула 26 and Формула 27. The dashes to the left and/or right of R, D, and F denote the permutations of their hatched and/or unprimed coordinates.

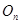The Fock coordinate function for a quasi–spin multiplet, averaging over which, as it turned out, is the minimal basis that the Rutanov terms gives, is constructed by reducing the basis of the Fock functions of the unitary group, Формула 28, to the irreducible basis of its orthogonal subgroup, Формула 29 [41].

The Hamiltonian of an open–shell multielectronic system in this method has the form proposed by Rutan [34, 35], which is essentially corrected to describe the averaged quasispin multiplet in [41] based on the ideas of Rakah [48]:

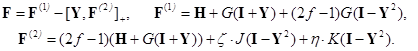
Формула 30

Here, I + Y is the charge and bond order density matrix, I - Y2 is the same for the open shell, F is the single Fock operator of this method, H is the energy matrix of the nuclear core, J and K are linear matrix operations describing the Coulomb and exchange interactions acting on the charge distribution indicated in brackets, and G = J + K. Optimized orbitals (or matrix Y) and energy Eξη characterizing the averaged quasispin multiplet can be found from the matrix equations of the self–consistent field (SCF):

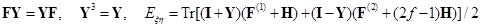
Формула 31

recorded in the applicable atomic basis. Numeric constants f, ζ and η depend on the number of electron pairs n (n can be half–integer) in an open shell, on the degree of degeneracy m, including their random degeneracy, on spin s, and on the number of precedence ν, ν = s, ..., n.

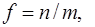
Формула 32
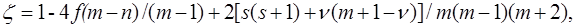
Формула 33
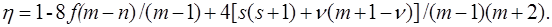
Формула 34

Details of the methods used in the derivation can be found in the article [41].

5. Tasks to be solved when creating a single software package

In a unified approach of the Fock coordinate function and density matrix, a software product will be developed in which it is necessary:??

  1. Implement the limited Hartree–Fock–Rutan method with automatic selection or calculation of the coefficients needed for the energy and Fokian functional to effectively take into account the limited configuration interaction for the open shell of each calculated state.
  2. Guarantee the preservation in the process of calculating a certain filling of self–consistent degenerate orbitals by designing the density of the open shell on the orbital subspace of a certain symmetry,
  3. Adapt the design method for calculating excited states.
  4. Implement limited configurational interaction for calculating the multiplet states of nanotubes and fullerenes so that, in the presence of random degeneration of the boundary orbitals, it is possible to maintain this degeneracy in the process of self–consistency.
  5. For guaranteed convergence of the iterative method for solving similar BSC equations and accelerate the self–consistency process, study the applicability of the scaling methods [51 – 53].
  6. Evaluate the effectiveness of the limited configuration interaction in the calculation of fullerenes and nanotubes, and using the existing programming language, if possible, graphically display the structure of the carbon cluster, the distribution of charge and spin densities in it.

While developing a separate software product, the tasks described above are performed. The user will be given the opportunity, by using the package interface, to carry out calculations of different states of a carbon cluster with an open (or closed, as a special case) shell and evaluate the role of configuration interaction in determining, in the end, its ground and excited electronic states.

Conclusions

In this master's thesis, the relevance and novelty of the tasks to be solved are substantiated. The selected object of study is promising for practical applications for a new class of compounds – fullerenes and nanotubes. Diversity their volumetric forms are marked and the abundance of compounds synthesized on their basis, identifying the usefulness of the use of properties, including in medicine.

The goals and objectives of this thesis are listed above.

Not resolved tasks, but important for improving the developed method, are:

  1. The question of the possible reason for the presence of random symmetry in highly symmetric molecular systems, like atoms with a d shell [49, 50], and the conditions for its removal while maintaining cluster symmetry.
  2. Investigate if the system with an open shell has a symmetry axis in a degenerate state third–order possibility of the appearance of universal instability for him, that is, the transition of the system into a stable, self–consistent state with symmetry breaking.
  3. The ability to preserve the advantages of the algorithm for calculating Rutanian states averaged over quasispin multiplet, when creating an effective method for calculating pure spatial symmetries of the state, as, for example, in the Hartree – Fock method extended along the spin.

Note

The abstract is made before research's completion, future changes are possible.

References

  1. E. Schrodinger. Quantisierung als Eigenwertproblem (Erste Mitteilung) // Annalen der Physik. – 1926. – Vol. 384 (79). – P. 361 – 376. Русский перевод: Э. Шрёдингер. Квантование как задача о собственных значениях (первое сообщение) // УФН. – 1977. – Т. 122. – С. 621 – 632.
  2. W. Heisenberg. Uber quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen // Zeitschrift fur Physik. – 1925. – Vol. 33, № 1. – P. 879 – 893. Русский перевод: В. Гейзенберг. О квантовотеоретическом истолковании кинематических и механических соотношений // УФН. – 1977. – Т. 122, вып. 8. – С. 574 – 586.
  3. W. Heisenberg. Uber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik // Zeitschrift fur Physik. – 1927. – Vol. 43, № 3 – 4. – P. 172 – 198. Русский перевод: В. Гейзенберг. О наглядном содержании квантовотеоретической кинематики и механики // УФН. – 1977. – Т. 122, вып. 8. – С. 651 – 671.
  4. Dirac P.A.M. The Quantum Theory of the Electron // Proc. Roy. Soc. (London), 1928, V. 117, P. 510 – 624. The Quantum Theory of the Electron (part II) // Proc. Roy. Soc. (London), 1928, V. 118, P. 351 – 361.
  5. Heitler W., London F. Wechselwirkung neutral Atome und homoopolare Bindung nach der Quantenmechanik. // Z. Phys., 1927, Bd 44, S. 455 – 472.
  6. Хаммермеш М. Теория групп и её применение к физическим проблемам – Москва: Мир, 1966. – 587 с.
  7. Каплан И.Г. Симметрия многоэлектронных систем. – Москва: Наука, 1969. – 407 с.
  8. Shavitt I. Graph Theoretical Concepts for the Unitary Group Approach to the Many – Electron Correlation Problem // Int. J. Quantum. Chem., 1977. S. 11. P. 131 – 148.
  9. Shavitt I. Matrix Element Evaluation in the Unitary Group Approach to the Electron Correlation Problem // Int. J. Quantum. Chem., 1978. S. 12. P. 5 – 32;
  10. Климко Г.Т., Лузанов А.В. Решение проблемы определения спиновых свойств молекул в унитарном формализме квантовой химии. // Журн. Структурн. Химии. – 1987. – т. 28, № 5. – с. 3 – 9.
  11. Вигнер Е. Теория групп и её приложения в квантовомеханической теории атомных спектров. – Москва: И.Л., 1961. – 443 с.
  12. Luzanov A.V. Matrix–Covariant Representation of High–Oder Configuration Interaction and Coupled Claster Theories // Int. J. Quantum. Chem., 2008, V. 108, N 4. P. 671 – 695.
  13. Бочвар Д. А., Гальперн Е.Г. Электронная структура молекул С20 и С60 // ДАН СССР Серия химическая. 1973. Т. 209, №3. С. 610–615.
  14. Корнилов М.Ю. Структура и свойства трубчатых углеводородов / М.Ю. Корнилов // Доклады АН УССР, серия «Б». – 1977. – Т.12. – с. 1097 – 1102.
  15. Кrotto H.W. Struсture of C60 moleсule / H.W. Кrotto // Nature. – 1992. – V. 358. – Р. 220 – 225.
  16. S. Iijima, Helical microtubules of graphitic carbon // Nature, – 1991, – V. 354. P. 56
  17. Структура, хартри–фоковская стабильность, антисимметричные решения, спектры основного и ионизированного состояний альтернантного архимедова тела С48 / Местечкин M.M., Климко Г.Т., Вайман Г.Е., Паничкина В.А. // Журн. структ. химии. – 1992. – Т. 33, №2. – С. 8 – 14. (J. Struct. Chem. – 1992. – V. 33, № 2. – p. 161 – 166, (translated from Russian).)
  18. Кузубов А.А. Электронная и атомная структура изомеров эндо– и экзоэдральных комплексов фуллеренов с двумя атомами лития / А.А. Кузубов. П.В. Аврамов, С.Г. Овчинников, С.А. Варганов, Ф.Н. Томилин // ФТТ. – 2001. – Т. 43. – с. 1721–1726.
  19. Mestechkin M.M., Klimko G.T. C28 is fullerene with possible quintet ground state // Mol. Mat. C. – 1996. – Vol. 8. – P. 165 – 168.
  20. Huffman D.R., Кraetschmer W., Lamb L.D., Fostjroрoulos К //Nature. 1990. V.347. P.354–358
  21. Вaun R.M. //Chem. Eng. New. 1985. V. 63. 1 51. P.20–29.
  22. Тaylor R., Hare J.P., Аbdul–Sada А.К., Кroto H.W. //J. Chem. Soc., Chem. Commun. 1990. P. 1423–1431
  23. Сидоров Л.Н., Болталина О.В. //Успехи химии. 2002. Т.71. 17. С.611–640.
  24. Соколов В.И., Станкевич И.В. //Успехи химии. 1993. Т.62. №5. С.455–472.
  25. Дикий В.В., Кабо Г.Я. //Успехи химии. 2000. Т.69. № 2. С.107–117.
  26. Елецкий А.В. //Успехи физических наук. 2000. Т.170. № 2. С.113–129.
  27. Караулова Е.Н., Багрий Е.И. //Успехи химии. 1999. Т.68. №11. С.979–998.
  28. Конарев Д.В., Любовская Р.Н. //Успехи химии. 1999. Т.68. №.1. С.23–44.
  29. Мюллер А., Рой С. //Успехи химии. 2002. Т.71. №12. С.1107–1119.
  30. EDITORIAL Diagnosis of the Fullerene Fever on the Occasion of the 1996 Nobel Prize in Chemistry // Fullerene science and technology, V. 5, N 1, P. iii – v.
  31. Винокуров С.Ф., Новиков И.Н., Усатов А.В. //Геохомия. 1997. С.937–940.
  32. Вecker L., Poreda R.J., Hunt А.J., Вunch Т.E., Ramрjno M. //Scjence. 2001. Т.291. С.1530–1533.
  33. Масайтис В. Л. //Региональная геология и металлогения. 1993. №1. С.121–125.
  34. Roothaan C. C. J. Self–Consistent Field Theory for Open Shell Electronic Sistems // Rev. Mod. Phys., 1960. – V. 32, N 1. – P. 179 – 186.
  35. Roothaan C. C. J., Hinze I. Multi–configurational selfconsistent field theory. // Progr. Theor. Phys.Suppl., 1967, V. 40, P. 35 – 50.
  36. Fukutome H. Theory of the unrestricted Hartree – Fock equation and its solutions. // Prog. Theor. Phys., 1974, – V. 52, N 1. – P. 115 – 130; N 6. – P. 1766 – 1783; 1975, – V. 53, N 5. P. 1320 – 1336.
  37. Mestechkin M.M., Whyman G.E. Matrix Formulation of the Generalized Hartree – Fock Methods // Int. J. Quantum Chem., 1974, V. 8 N 1. P. 45 – 60.
  38. Местечкин М. М. Метод матрицы плотности в теории молекул. Киев: Наук. Думка, 1977. – 352 с.
  39. Местечкин М. М. Нестабильность уравнений Хартри–Фока и устойчивость молекул. Киев: Наук. Думка, 1986. – 176 с.
  40. The Origing of Energy Functional in Roothaan Open Shell RHF Theory / Klimko G.T., Mestechkin M.M., Plakhutin B.N., Zhidomirov G.M. // Int. J. Quantum. Chem. – 1990. – V. 37, № 1. – P. 35 – 50.
  41. Klimko G.T., Mestechkin M.M. Roothaan’s Open Shell Theory from the Viewpoint of an Orthogonal Group. // Int. J. Quantum. Chem. – 1990. – V. 37, № 5. – P. 753 – 771.
  42. Mestechkin M.M., Klimko G.T. Spin–dependent operators in the spin–free quantum chemistry // Intern. J. Quantum Chem. – 1978. – V. 13, № 5.–P.579–596.
  43. Klimko G.T., Mestechkin M.M., Whyman G.E. Fock coordinate function method for separation of spin variables in transition density matrices // Intern. J. Quantum Chem.–1980. – V. 17, № 3. – P. 415 – 428.
  44. Mestechkin M., Whyman G., Klimko G. Nonlinear optical properties of alternant fullerene C48 // Fullerene science and technology, 1997. – V. 5, N 1, P. 195 – 203.
  45. Фок В.А. О волновых функциях многоэлектронных систем // Журн. Эксперим. и теорет. физ. – 1940. – Т. 10, № 9 – 10. – С. 961 – 979.
  46. Фок В.А. Начала квантовой механики. – М.: Наука, 1976. – 376 с.
  47. Климко Г.Т., Местечкин М.М. Суперпозиция конфигураций и метод координатной функции Фока. // Многоэлектронная задача в квантовой химии (Сб. научных трудов), Наук. Думка, Киев. – 1987. – с. 31 – 43.
  48. Rakah J. Theory of Complex Spektra. IV. // Phys. Rev., 1949. – V. 76, N 9. – P. 1352 – 1365.
  49. Климко Г.Т. О применимости молекулярных методов для расчета атомов с открытыми оболочками. // Журн. физич. химии. – 1996. – т. 70, № 4. – с. 667 – 674.
  50. Климко Г.Т. К проблеме случайного вырождения термов в d– оболочке. // Журн. физич. химии. – 1999. – т. 73, № 3. – с. 507 – 512.
  51. Фаддеев Д. К. Вычислительные методы линейной алгебры / Д. К. Фаддеев, В. Н. Фаддеева. – Санкт–Петербург: Лань, 2002. – 736 с.
  52. Баркалов К.А. Методы параллельных вычислений/ К.А. Баркалов. –Н.Новгород: Изд–во Нижегородского университета им. Н.Лобачевского, 2012. – 124 с.
  53. Бахвалов Н.С. Численные методы / Н. С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. – Москва: БИНОМ. Лаборатория знаний, 2008. – 636 с.